2018 International Conference on Computer, Communications and Mechatronics Engineering (CCME 2018) ISBN: 978-1-60595-611-4
A Second-order Energy Stable Fourier Spectral Method for the
Fractional Cahn-Hilliard Equation
Li-quan MEI* and Yan HOU
School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an, 710049, P.R. China *Corresponding author
Keywords: Fractional Cahn-Hilliard equation, BDF2, Convex splitting, Energy stable, Spectral
method.
Abstract. In this paper, we presented a second order accurate (in time) energy stable numerical scheme for the Fractional Cahn-Hilliard (CH) equation. Combining the convex splitting method, we applied the implicit backward differentiation formula (BDF2) to derive second order temporal accuracy, and we used the Fourier spectral method for space discrete to obtain the fully discretization scheme. Then we discussed the unique solvability and energy stability. A few numerical experiments were presented to conclude the article.
Introduction
The Cahn-Hilliard equation was introduced by Cahn and Hilliard in [1] to describe the complicated phase separation and coarsening phenomena in a solid [2] and then extended to many other physical phenomena, such as image processing [3], planet formation [4] and so on, which are perhaps the most well-known of the gradient flow-type PDEs. Recent studies show that non-homogeneities of the medium may fundamentally alter the laws of Markov diffusion, leading to long range fluxes, and non-Gaussian, heavy tailed profiles, and these motions may no longer obey the classical Fick’s law. This phenomenon is called anomalous diffusion. Fortunately, fractional diffusion equations provide an adequate and accurate description of transport processes that exhibit anomalous diffusion. Subsequently, fractional diffusion equations have been applied in increasingly more applications [5, 6]. Bosch and Stoll [7] presented the fractional Cahn–Hilliard equation for gray value image inpainting.
In this paper, we focus on the following fractional-in-space Cahn-Hilliard (CH) equation
2
0
( ) ( ( )) 0, (0, ]
( , 0) ( ), , u
u f u in T
t
u x u x x
(1)
wherex( ,x1 ,xd),d 1, 2,3,
0 1
( )
per
u L H , is a positive constant that dictates the interface width, f u( ) F u'( )u3u.For any 1
( )
uH , the CH energy functional is given by
2 2
( ) ( | | ( )) 2
E u u F u dx
The Semidiscrete Scheme
In this section, we present an unconditionally stable Fourier spectral method to simulate the asymptotic behavior of solution for the fractional Eq. (1). The proposed method is based on the BDF2 formula for temporal discrete.
In order to solve the Fractional CH equation accurately and efficiently, we use the convex splitting method [8] to split the energy functional (2) into two convex functionals.
2 2
( ) ( ) ( ), ( ) ( | | ( )) , ( ) ( ) ,
2
c e c e
c e
E u E u E u E u u u dx E u u dx
(3)where 1 4 1 2
( ) , ( )
4 2
c u u e u u
, let the chemical potential 2
( )
w u f u .The second order convex
splitting BDF method can be written as
1 1
1
1 2 1 1 3 1
3 4
( ) , 2
( ) (2 ),
n n n
n
n n n n n
u u u
w
w u u u u
(4)
the initialization step is as follows: given 0
u , find 1
u , such that
1 0
2 1 0 3 0
( ) ( ( ) ).
u u
u u u
(5) For the convex splitting BDF scheme (4)-(5), we have the following mass conservation.
Theorem 1.For any 0, the convex splitting BDF scheme (4)-(5) is mass conserving.
Proof. Integrating (5) on , according to () 1 0 [9], we have 1 0
(u u dx) 0
, therefore, 1 0u dx u dx
Integrating (4), we obtain
1 0
.
n n
u dx u dx u dx
This completes the proof.Theorem 2. The convex splitting BDF scheme (4)-(5) is uniquely solvable for any time step 0.
Proof. Consider the following functional
1 2 1
1
( ) || 3 4 || ( ) 2 ( (2 ), ) 2
n n c n n
G u u u u E u u u u
It may be shown that n1
u H is the unique minimizer of G u( ) if and only if it solves, for any
0
vH ,
2
1 3 1
0
1
( ) | (3 4 , ) 2 ( , ) 2 ( , ) 2 (2 , ) 2
(3 4 2 ( ) , ) ,
n n n n n
s
n n
dG
u sv u u u v u v u v u u v
ds
u u u w v
where 2 3 1
(2 n n ).
w u u u u
Because the functional G is strictly convex by
2 2
2 0
2 2
1
( ) | || || ( ( ) , ) 0.
2
c s
d G
u sv v E u v v
ds u
(6) Therefore, for any vH0,
0
( ) |s 0
dG u sv
ds
if and only if the given equation holds (4). Hence,
minimizing the strictly convex functional G u( )is equivalent to solving eq. (4), un1is the unique minimum point, i.e. the unique solution. This completes the proof.
Theorem 3. Suppose that n1
u is a solution to (4)-(5). The convex splitting BDF scheme (4)-(5) is unconditionally energy stable, meaning that for any time step size 0
0
( n) ( ).
E u E u (7)
Limited to space, we omit the details of the proof.
Fourier Spectral Fully-discrete Scheme
After discretizing governing equations in time as described in above section, now we will further give the fully-discrete scheme based on Fourier spectral method.
Let klm ( , , , )
n
k l m
u u x y z n , based on Fourier spectral method
/ 2
, , /2
ˆ
klm kl
N
n n ikx ily imz k l m N
u u e
. (8) From the definition of fractional Laplace operator ()[9], we can obtain the following fully-discrete convex splitting BDFscheme for Eq. 1
1 1
2 2 2 1
1 2 2 2 2 1 1 3 1
ˆ ˆ ˆ
3 4
ˆ
( (( ) ( ) ( ) )) , 2
ˆ (( ) ( ) ( ) )ˆ (ˆ ) (2ˆ ˆ ).
n n n
n klm klm klm
klm
n n n n n
klm klm klm klm klm
u u u
ik il im w
w ik il im u u u u
(9) Numerical Experiments
Accuracy Check and Convergence Test
We first consider the 2D problem on 2 [0, 2 ] ,
1/ 10 and the initial condition u0sin sinx y.
In order to verify the numerical accuracy, we choose different N20,30,40,50,60,70,80, The ratio for the estimated space convergence rate can be written as
1 2
1 2
log(|| ( , ) || / || ( , ) ||) . log( / )
N
E N E N
R
N N
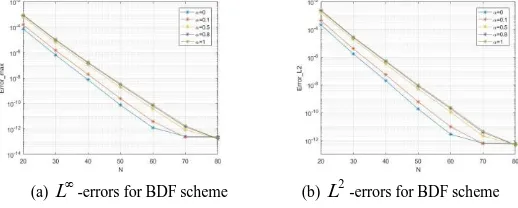
[image:3.595.165.424.560.664.2](10) Figure 1 shows the L- and 2
L-errors with respect to various N. The results reveal that the space convergence of the proposed scheme is exponential convergence and independent with the fractional order .
(a) L-errors for BDF scheme (b) L2-errors for BDF scheme
Figure 1. Numerical errors at t=1.0 plotted versus n, 3 10
.
Take different time step 1/200, 1/400, 1/600, 1/800, 1/1000, the estimated temporal convergence rate is written as
1 2
1 2
log(|| ( , ) || / || ( , ) ||) . log( / )
E N E N
R
Figure 2 shows the L- and 2
L-errors with respect to various . The results reveal that the temporal
convergence rate of the convex splitting scheme is close to 2 and independent with the fractional order .
[image:4.595.163.427.119.225.2]
(a) L-errors for BDF scheme (b) L2-errors for BDF scheme
Figure 2. Numerical errors at t=1.0 plotted versus , N64.
Next, we take 0.1,0.5,N32, 0.001 and the initial condition 0
0.1sin sin
u x y. The energy for can be calculated as
2
2 3
( ) ( | | ) . 2
E u u u u dx
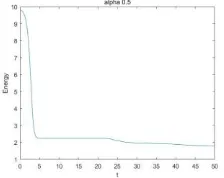
(12) Figure 3 shows the time evolutions of the energy functional for the fractional CH equation. It validates the proposed convex splitting scheme is energy stable.
Figure 3. The temporal evolutions of the energy.
Simulations of Interaction Process of Two Air Bubbles
A numerical simulation result of a physics example is presented in this subsection. We simulate the interaction process of two air bubbles by using the proposed numerical scheme for the fractional Cahn-Hilliard equation. We take 0.1,N256, 0.001 and the initial condition
2 2 2 2
0 1, ( 1) ( ) 1 ( 1) ( ) 1
( , )
1,
x y x y
u x y
others
[image:4.595.241.353.349.438.2](a) 0.
[image:5.595.72.514.69.276.2](b) 0.5
Figure 4. Snapshots of the interaction of two air bubbles.
Numerical Simulations of Coarsening Process
The coarsening process [10] is simulated in this subsection. We compare the numerical simulation result with the predicted coarsening rate using the proposed second order convex splitting BDF Fourier spectral scheme for the fractional Cahn-Hilliard flow. We take 0.1,N256,0.001 and the random initial condition [11]
0
( , ) (2 1) 0.02 [ 10,10]
u x y random , (13)
where 0.5, 0.75 respectively.
Figure 5 presents time snapshots of the phase variable . A significant coarsening process is clearly observed in the system.
(a) 0.1,0.5,T5 (b) 0.1,0.5,T 10 (c) 0.5,0.5,T5 (d) 0.5,0.5,T10
(e) 0.1,0.75,T10 (f) 0.1,0.75,T 20 (g) 0.5,0.75,T10 (h) 0.5,0.75,T20
Figure 5. Snapshots of the coarsening process in 2D.
Next, we simulate a 3D coarsening problem described by 3 dimensional fractional Cahn-Hilliard equation using the proposed second order convex splitting BDF Fourier spectral scheme. We take
0.1,N 64, 0.002
and the random initial condition 0 ( , , )
[image:5.595.64.531.464.662.2](a) 0.1,0.5,T 5 (b) 0.1,0.5,T10 (c) 0.5,0.5,T5 (d) 0.5,0.5,T 10
[image:6.595.73.524.73.264.2](e) 0.1,0.75,T10 (f) 0.1,0.75,T 20 (g) 0.5,0.75,T10 (h) 0.5,0.75,T 20
Figure 6. Snapshots of the coarsening process in 3D.
Conclusions
In this work, combined Fourier spectral method with convex splitting technique, a new numerical scheme for the approximation of the fractional-in-space CH equation is presented. The mass conservation, unique solvability and energy stability of the scheme are studied. The computations we performed demonstrated that this method is very effective and capable of giving very accurate and stable results.
Acknowledgment
This work is supported by the National Nature Science Foundation of China, No. 11371289.
References
[1] J.W. Cahn and J.E. Hilliard, “Free energy of a non-uniform system I. Interfacial free energy”, J. Chem. Phys. Vol.28, pp. 258–267,1958.
[2] B.P. Vollmayr-Lee and A.D. Rutenberg, “Fast and accurate coarsening simulation with an unconditionally stable time step”, Phys. Rev. E, vol. 68 (066703), 2003.
[3] I.C. Dolcetta, S.F. Vita and R. March, “Area-preserving curve-shortening flows: from phase separation to image processing”, Interfaces Free Bound, vol. 4, pp. 325–343, 2002.
[4] M. Paniconi and K.R. Elder, “Stationary, dynamical and chaotic states of the two-dimensional damped Kuramoto–Sivashinsky equation”, Phys. Rev. E, vol. 56, pp. 2713–2721, 1997.
[5] P.W. Bates, “On some nonlocal evolution equations arising in materials science”, in: Nonlinear Dynamics and Evolution Equations, in: Fields Institute Communication, vol. 48, American Mathematical Society, Providence, RI, pp. 13–52, 2006.
[6] G. Akag, G. Schimperna and A. Segatti, “Fractional Cahn–Hilliard, Allen-Cahn and porous medium equations”, J. Differ. Equations, vol. 261, pp. 2935–2985, 2016.
[7] J. Bosch and M. Stoll, “A fractional inpainting model based on the vector-valued Cahn–Hilliard equation”, SIAM J. Imaging Sci. vol. 8, no.4, pp. 2352–2382, 2015.
[9] Bueno-Orovio, D. Kay and K. Burrage, “Fourier spectral methods for fractional-in-space reaction-diffusion equations”, BIT Numer. Math., vol. 54, no. 4, pp. 937–954, 2014.
[10] Y. Yan, W. Chen, C. Wang and S. M. Wise, “A Second-Order Energy Stable BDF Numerical Scheme for the Cahn-Hilliard Equation”, Commun. Comput. Phys., vol. 23, no.2, pp. 572-602, 2018.