Determining lake surface water temperatures worldwide using a tuned one-dimensional lake model ( FLake(, v1)
Full text
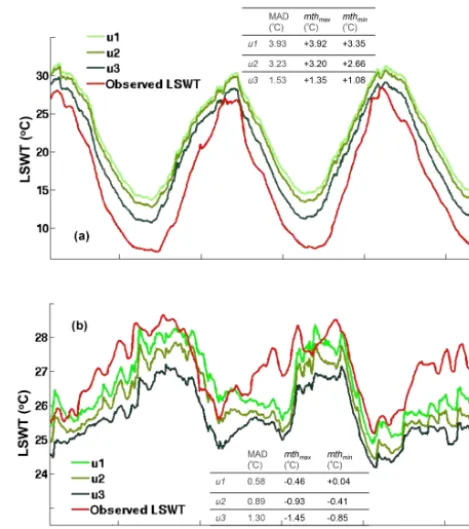
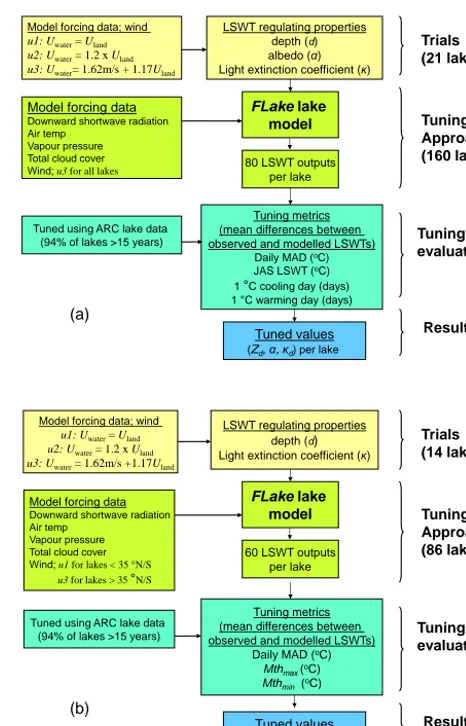
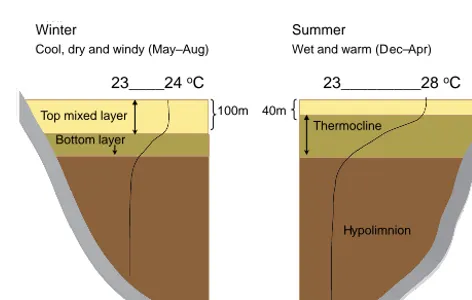
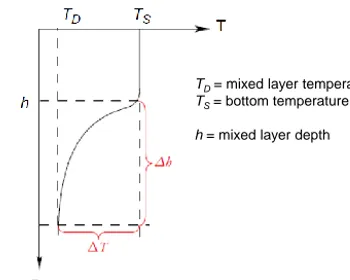
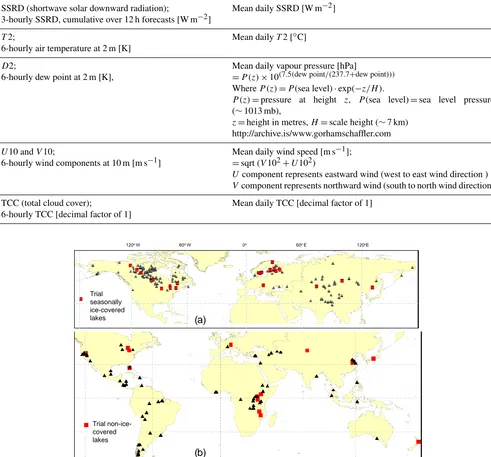
Figure
Related documents
12 Analyzing the risk taking behavior of fund managers using portfolio holdings allows us to examine the fund manager’s intended rather than the realized change in risk..
Geophysical - Electromagnetic - Magnetometer - Radiometric - Other Geological Geochemical Geophysical - Electromagnetic - Magnetometer - Radiometric - Other
Morphometric analysis of small arteries in the human retina using adaptive optics imaging: relationship with blood pressure and focal vascular changes. The arrangement of the
ambipolar diusion length as a function of VHF power for the two dilution series (at 6 and 30 W) and the two power series (at 5% and 7.5% silane concentration). For the two
1) Remove wheel and brake drum. Remove tension spring, hold- down springs, pins, brake shoes, adjuster assembly, spring and strut. 2) Disconnect parking brake cable from adjuster
That was our conclusion after researching the social media sites on which readers are most likely to share content from our blog focused on solutions to a wide range of
Importantly, just before the development of the new dental hygiene curriculum, librarians at the main IUPUI campus library, University Library, had developed a common curriculum
Dynamics of number of small and medium-sized enterprises and social enterprises (Source: Lithuanian Statistics under the Ministry of Social Security and Labour) Small and