Material Dependence of the Thermoelectric Figure of Merit
*1Yukari Katsura
1,2,*21Department of Frontiers Science, The University of Tokyo, Kashiwa 277–8561, Japan
2Center for Materials research by Information Integration, National Institute for Materials Science, Tsukuba 305–0047, Japan First-principles calculations were used to perform a cross-material investigation on the electronic structures of 13 parent compounds for thermoelectric materials. Boltzmann transport equations were used to calculate carrier doping level dependence of the Seebeck coefficient, electrical conductivity with respect to relaxation time, effective Lorenz numbers and the maximum possible thermoelectric figure of merit (ZeT)
in the limit of zero phonon thermal conductivity. High ZeT was obtained only in semiconductors with finite band gaps. High ZeT for high doping
level was achieved in compounds that had a steep density of states at the band edge. Calculations were combined with experimental transport properties to evaluate electron relaxation time of the samples. These analyses can be used to understand the nature of electron scattering mech-anisms in specific thermoelectric materials and reduce the number of experiments required to develop new thermoelectric materials. [doi:10.2320/matertrans.MF201612]
(Received April 4, 2016; Accepted April 14, 2016; Published June 3, 2016)
Keywords: thermoelectric materials, first-principles calculations, Boltzmann transport theory, scattering mechanism
1. Introduction
Thermoelectricity is a common phenomenon in nearly all semiconductors and metals. The discovery of new thermo-electric materials is essential to overcome the practical prob-lems associated with current thermoelectric conversion sys-tems, including performance, stability, toxicity and cost. An important parameter to describe thermoelectric materials is the thermoelectric figure of merit1) (ZT), defined as:
ZT = S
2σT
κel+κph,
where S is the Seebeck coefficient, σ is electrical conductivi-ty, κel is electron thermal conductivity, κph is phonon thermal
conductivity and T is temperature. A high ZT is required to achieve high conversion efficiency; a typical criterion for ap-plication is ZT > 1.
Researchers searching for new thermoelectric materials must assess the potential of the parent compounds, which re-quires optimization of the dopant elements, doping level, and microstructure of the compound. It is possible that many ma-terials have been regarded as low-ZT compounds simply be-cause the optimal doping and microstructure conditions were not deduced experimentally. Prediction of the doping-level dependence of thermoelectric properties is important to make the search for new materials more efficient. Theoretical cal-culations, including multi-valley structure2), low-dimensional
material3), quantum well4), phonon–glass–electron–crystal5)
and pudding-mold band (flat-band)6) models, have influenced
experimental searches. Numerical solutions to the Boltzmann transport equations have also been employed. Using this ap-proach, S, σ/τel and κel/τel are obtained (usually as functions
of chemical potential) and can be converted into the net carri-er concentration (carricarri-er doping level) n. The unknown factor
τel is called the electron relaxation time, which corresponds to
the time interval between electron scattering events.
Unfortu-nately, this factor is not frequently calculated using first-prin-ciples approaches, depends on T7,8) and varies by orders of
magnitude by adding extrinsic electron scattering centers such as impurities, defects and grain boundaries.
There are two ways to obtain transport distribution func-tions (TDFs), or spectral conductivity, which is required for Boltzmann transport analysis. One method for involves using artificial TDFs such as delta-functions9), rectangular
func-tions10) and step functions11). In studies that employ this
method, the TDFs that achieved high ZT were characterized by a nearly-zero TDF at the Fermi level EF and a steep change
in the TDF near EF. The other method to obtain TDFs is to use
first-principles calculations on real crystal structures. A num-ber of sophisticated calculations have been performed on var-ious thermoelectric materials12–15). However, each of the
pre-vious studies has considered only a few compounds, employed a different calculation method and was presented on a differ-ent scale. Previous studies were not focused on cross-material investigation of calculated properties, which is necessary for the search for new materials.
In this study, we have calculated the thermoelectric proper-ties of various known thermoelectric materials to reveal the electronic structures of suitable parent compounds for ther-moelectric materials. Because ZT was difficult to calculate from first-principles, we focused on ZeT = S 2σT/κel, which is
the maximum possible ZT in the limit when κph is much less
than κel. It is important that ZeT is always higher than ZT, so
that high ZeT values are not physically meaningful. Low ZeT
values are important because they allow us to exclude un-promising materials from the list of target materials. For ex-ample, to obtain a compound with ZT > 1, parent compounds with ZeT < 1 should be excluded.
2. Calculation Method
First-principles calculations were performed on the 13 par-ent compounds, listed in Table 1, using atomic positions and experimental lattice parameters from the Inorganic Crystal Structure Database (ICSD)18). Electronic structures were
cal-culated using the full-potential linearized augmented plane-*1
This Paper was Originally Published in Japanese in J. Japan Inst. Met. Mater. 79 (2015) 633–637.
*2
Corresponding author, E-mail: katsura@k.u-tokyo.ac.jp
Special Issue on Recent Progress in Thermoelectrics -New Analyses and New Materials- (Thermoelectric Conversion Materials IX)
wave method implemented in WIEN2k19) and employed
gen-eralized gradient approximation (GGA)20) followed by
Tran–Blaha modified Becke–Johnson (TB–mBJ)21)
ex-change-correlation potentials. Dense k-meshes were selected to reduce oscillatory noise in n-dependences of the calculated transport properties. Convergence criteria for energy, charge and forces were 0.0001 Ry, 0.0001 e and 1 mRy/atom, re-spectively. Atomic coordinates were optimized during calcu-lations. Lattice parameters were not optimized because they are inaccurate in layered compounds with van der Waals bonding. Spin–orbit interaction was introduced for anions heavier than 5p elements. Spin polarization was not consid-ered in any of the calculations. The density of states (DOS) was normalized by reduced the unit cell volume Vcell to allow
for comparison with compounds with different unit cell sizes. The Boltzmann transport equations were solved using BoltzTraP22). We obtained σ/τ
el, S and κel/τel as functions of
carrier doping level n = |nhole − nelectron|, which was calculated
by dividing the number of additional electrons in the unit cell by Vcell. The BoltzTraP code was modified to include the
sec-ond term (Peltier term) for κel/τel7,8,23). From these values, the n-dependences of effective Lorenz number Leff was
calculat-ed as
Leff = κel σT =
(κel/τel) (σ/τel)T
and ZeT was calculated as
ZeT = S 2σT
κel =
S2(σ/τel)T (κel/τel) =
S2 Leff .
ZeT is the theoretical upper limit of ZT, which is given by
ZT = S
2σT
κel+κph =
S2(σ/τ el)T (κel/τel)+(κph/τel),
where κph/τel → 0. Temperature dependences calculated in
this study included only the effects of the Fermi–Dirac distri-bution function, thus ignoring changes in lattice parameters, phase transitions and decompositions of the compounds.
To understand the difference between ZeT and ZT, we
cal-culated ZT using an arbitrary value for κph/τel. The actual
val-ue of κph/τel would depend on T, the material families and the
scattering probabilities of phonons and electrons in each sam-ple.
3. Results and Discussion
3.1 Material dependence of transport properties
Normalized DOS calculated for 12 parent compounds are presented in Fig. 1(a). All of the compounds had finite Eg
us-ing both GGA and TB–mBJ, but TB–mBJ tended to repro-duce the experimental Eg better, as shown in Table 1. We
ob-served a material dependence in the gradient of normalized
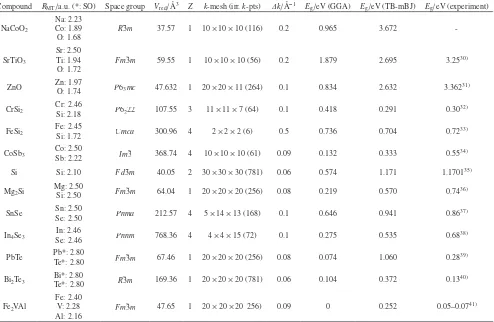
Table 1 Calculation conditions and the calculated/experimental band gaps (Eg) of the thermoelectric materials. RMT is the muffin-tin radius of each element, Vred is the reduced cell volume and FU is the number of formula units per reduced cell. The column k-mesh indicates the numbers of divisions of the first
BZ (k-mesh, first line), numbers of irreducible k-points in the k-mesh (irr. k-pts, second line, in parentheses), and the average k-spacing Δk in the raw cal-culations (Δk/Å−1, third line). Note that effective Δk for transport calculations was 1/5 of the presented values because of the k-point interpolation employed
by BoltzTraP.
Compound RMT/a.u. (*: SO) Space group Vred/Å3 Z k-mesh (irr. k-pts) Δk/Å−1 Eg/eV (GGA) Eg/eV (TB-mBJ) Eg/eV (experiment)
NaCoO2
Na: 2.23 Co: 1.89
O: 1.68 R¯
3m 37.57 1 10 × 10 × 10 (116) 0.2 0.965 3.672
-SrTiO3
Sr: 2.50 Ti: 1.94 O: 1.72
Fm¯3m 59.55 1 10 × 10 × 10 (56) 0.2 1.879 2.695 3.2530)
ZnO Zn: 1.97O: 1.74 P63mc 47.632 1 20 × 20 × 11 (264) 0.1 0.834 2.632 3.36231)
CrSi2 Cr: 2.46Si: 2.18 P6222 107.55 3 11 × 11 × 7 (64) 0.1 0.418 0.291 0.3032)
FeSi2 Fe: 2.45Si: 1.72 Cmca 300.96 4 2 × 2 × 2 (6) 0.5 0.736 0.704 0.7233)
CoSb3 Co: 2.50Sb: 2.22 Im¯3 368.74 4 10 × 10 × 10 (61) 0.09 0.132 0.333 0.5534)
Si Si: 2.10 Fd ¯3m 40.05 2 30 × 30 × 30 (781) 0.06 0.574 1.171 1.170135)
Mg2Si Mg: 2.50Si: 2.50 Fm¯3m 64.04 1 20 × 20 × 20 (256) 0.08 0.219 0.570 0.7436)
SnSe Sn: 2.50Se: 2.50 Pnma 212.57 4 5 × 14 × 13 (168) 0.1 0.646 0.941 0.8637)
In4Se3 Se: 2.46In: 2.46 Pnnm 768.36 4 4 × 4 × 15 (72) 0.1 0.275 0.535 0.6838)
PbTe Pb*: 2.80Te*: 2.80 Fm¯3m 67.46 1 20 × 20 × 20 (256) 0.08 0.074 1.060 0.2839)
Bi2Te3 Bi*: 2.80Te*: 2.80 R¯3m 169.36 1 20 × 20 × 20 (781) 0.06 0.104 0.372 0.1340)
Fe2VAl
Fe: 2.40 V: 2.28 Al: 2.16
[image:2.595.55.549.124.446.2]DOS at the band edges. The gradient tended to be small in sp-semiconductors such as Bi2Te3, PbTe, Si, Mg2Si and
n-type ZnO. In contrast, the gradient was large in 3d transi-tion metal compounds such as FeSi2 and n-type SrTiO3, and
in materials with highly degenerate O 2p valence bands such as NaCoO2.
For all compounds, the calculated values of |S| monotoni-cally decreased with increasing n for high n, as shown in Fig. 1(b). Compounds with a larger gradient of normalized DOS exhibited large |S|. While n-type ZnO had very shallow conduction band edge and exhibited small S over the entire range of n, p-type NaCoO2 had a steep valence-band edge and
exhibited large S for a wide range of n.
In contrast to |S|, σ/τel monotonic increased with
increas-ing n and the values for σ/τel were higher in compounds with
a smaller gradient of normalized DOS, as shown in Fig. 1(c). Such material dependences in |S| and σ/τel can be explained
using the parabolic-band model7,8), where compounds with
greater effective mass exhibit larger |S| and lower σ/τel. The
changes in the orders of the compounds may originate from the difference in band degeneracy.
Figure 1(d) shows effective Lorenz number Leff. For some
compounds, Leff was close to the theoretical Lorenz number L0 = 2.45 × 10−8 V2K−2 (free electron model) at high n
(great-er than 1027 m−3). However, at lower n, the calculated L eff was
to approximately 80% of L0; the value of Leff at low n was
compound-dependant. These types of changes in Leff have
been noted as a general phenomenon in semiconductors24).
The small ripples observed in σ/τel of some compounds at
high n were due to the noises of Fourier expansion of band energies in BoltzTraP and they can be reduced by using a denser k-point mesh.
The calculated values of ZeT for T = 300 K are presented in
Fig. 1(e). The compounds that exhibited large |S| also exhibit-ed high ZeT, as expected from the expression ZeT = S 2/Leff.
The extremely high values of ZeT, such as ZeT > 100, at low n
are meaningless because the calculation ignored κph, which
dominants the total thermal conductivity at low n. Figure 1(g) shows an example calculation at 300 K, with κph/τel set to
1014 Wm−1K−1s−1 for all compounds. Achieving such a small
κph/τel is not very realistic because it requires the material to
maintain τel = 10−14 s, such as in single-crystal Si, and κph =
1 W m−1 K−1, such as in silica glass, at the same time.
How-ever, the data in Fig. 1(g) demonstrate that the introduction of the κph/τel term strongly suppressed the values of ZT from ZeT, especially at low n. Therefore, we can assume that
com-pounds with high ZeT at high n are more promising
com-pounds to achieve high ZT than comcom-pounds with low ZeT at
high n because ZT is less affected by κph/τel. An example of
such a compound is NaxCoO2, which is known to have a
rela-tively high optimum doping level as a thermoelectric materi-al. Phonon–glass–electron–crystal materials are another set of promising materials, as they have a low κph/τel, which
min-imizes the reduction of ZT from ZeT. Based on the positions
of the peaks in the ZT curves, we expect that optimum carrier
Fig. 1 (a) DOS of the 12 thermoelectric material parent compounds, normalized by unit cell volume. TB–mBJ was employed as the exchange-correlation potential. One grid along the vertical axes corresponds to normalized DOS of 1030 eVm−3. The letters in parentheses indicate the selected carrier types used
for the transport calculations. (b) n-dependence of the absolute Seebeck coefficients at 300 K. (c) n-dependence of electrical conductivity (σ) divided by τel. (d) n-dependence of effective Lorenz number. The black line indicates the theoretical value L0 obtained from the free electron model. (e), (f)
n-depen-dence of ZeT at (e) 300 K and (f) 900 K, assuming rigid crystal structures. (g) n-dependence of ZT at 900 K, assuming that κph/τel decreased to
1014 Wm−1K−1s−2 in all materials.
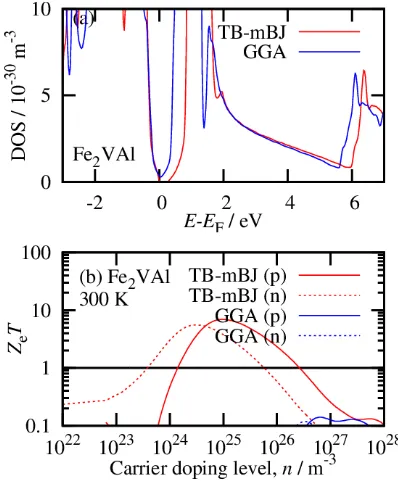
Fig. 2 (a) Normalized DOS and (b) n-dependence of ZeT of Fe2VAl,
[image:3.595.128.470.69.224.2] [image:3.595.325.524.309.550.2]doping level nopt is low in small-S compounds and high in
large-S compounds. This leads to an assumption that nopt in n-type ZnO is low, although it also depends on the value of
κph/τel.
3.2 Effects of thermal excitation over the band gap The effects of thermal excitation for compounds with nar-row band gaps such as CrSi2, CoSb3 and Bi2Te3 are
observ-able in Figs. 1(b) to (g). Thermal excitation, which is also referred to as the bipolar effect, reduces the positive S of hole carriers and the negative S of electron carriers, while increas-ing total carrier density. This effect is more critical for low n than for high n. At 300 K, the calculations predict that com-pounds with narrow Eg suffer from thermal excitation at
300 K, resulting in peaking behavior in the S–n curves. In contrast, at low n, σ/τel increased rapidly with increasing T,
indicating an increase in total carrier concentration (nelectron + nhole) due to thermal excitation. Notable increases in Leff are
observable in Fig. 1(d) because of the increase in κel as
addi-tional energy associated with Eg is carried by the electrons or
holes.
Although the effects of thermal excitation were not critical at 300 K for materials with wider Eg, the influence of thermal
excitation increased with increasing T. Figure 1(f) shows that, at 900 K, ZeT of many compounds was suppressed up to n = 1025–1026 m−3, which is the typical n for optimum doping.
At 900 K, many narrow-gapped semiconductors did not achieve ZeT = 1 over the entire ranges of n, indicating that the
compounds would not achieve ZT > 1 at 900 K without mod-ification or correction of the electronic structures. Therefore, to achieve ZT > 1, it is very important for the parent com-pound to have wide Eg. This criterion for Eg was presented by
Mahan et al. and is known as the 10 kBT rule25). At 300 K and
900 K, 10kBT is approximately about 0.25 eV and 0.75 eV,
respectively. Compounds with Eg less than 10kBT were
strongly affected by thermal excitation. Unfortunately, this finding reveals the limit of first-principles calculations for prediction of thermoelectric properties because the present first-principles calculations have large errors in Eg. An
exam-ple of such an error is shown in Fig. 2, which shows ZeT of a
narrow-gap Heusler alloy (Fe2Val) calculated using two
dif-ferent exchange-correlation potentials. When calculated us-ing TB–mBJ, Eg was as wide as 0.25 eV, while it was
calcu-lated as a pseudo-gap semimetal using GGA. This difference in Eg results in notable differences in the calculated ZeT
val-ues, for example, TB–mBJ produced ZeT = 10, while GGA
produced ZeT = 0.1. The GGA result cannot explain the
ex-perimental measured ZT, which exceeds 0.1. Thus, it is im-portant to ensure consistency between theoretical and experi-mental Eg to ensure the reliability of the calculations. This
can be challenging because experimental Eg values are not
always available.
3.3 Estimation of τel using experimental data
We attempted to estimate the unknown term κph/τel in the ZT expression by fitting calculation results with experimental data. As a preliminary study, we measured the experimental data Sexp(T), σexp(T), and κexp(T) of two Si0.8Ge0.2
polycrystal-line samples27,28). For each T, we used the TB–mBJ
calcula-tion for pure Si to find n such that Scalc(n, T) reproduced the
value of Sexp(T). Although the S–n curve typically exhibited a
monotonic decrease to yield a single solution for n, in some cases the thermal excitation bent the S–n curve to give two or more solutions for n. In such cases, we selected the n value by considering the experimental carrier concentration (typically 1026 m3) and whether the sample was influenced by thermal
excitation.
After we found the most probable n, we found the corre-sponding value for (σ/τel)calc and calculated τel as:
τel= σexp
(σ/τel)calc.
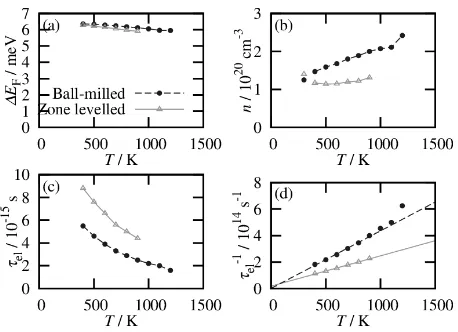
The results of this analysis are presented in Fig. 3. With increasing T, the estimated chemical potential (ΔEF) slowly
approached the middle of the band gap and then n increased. The value of τel for the zone-leveled sample was
approxi-mately 1 × 10−14 s at 300 K, which is very close to the
report-ed value for single crystalline Si29). The ball-milled sample
exhibited shorter τel, reflecting the increased frequency of
electron scattering. In both samples, τel was proportional to T −1, indicating that the acoustic distortion potential scattering
dominated other scattering mechanisms, such as ionized im-purity scattering. Although additional refinement of the cal-culation would improve the calcal-culation accuracy, such analy-sis could reveal the nature of scattering phenomenon in real thermoelectric materials.
4. Conclusion
First-principles calculations and Boltzmann transport anal-ysis were used to perform a cross-material investigation over 13 parent compounds of thermoelectric materials. We con-firmed that compounds with Eg greater than several kBT and
steep a DOS at the band edge exhibited high ZeT, which is a
necessary condition for a compound to achieve high ZT. 3d transition metal compounds and p-type oxide thermoelectric
Fig. 3 Transport properties of the p-doped Si0.8Ge0.2 polycrystalline
sam-ples estimated using experimental data to fit the calculated data. The ball-milled sample is sample No. 93 in Ref. 27), with κph = 1.89 Wm−1K−1 and ZT = 0.53 at 900 K. The zone-leveled sample is sample No. 1834 in Ref. 28), with κph = 2.65 Wm−1K−1 and ZT = 0.69 at 900 K. (a)
T-depen-dences of estimated offsets of the chemical potential EF from the center of
the band gap. (b) T-dependences of estimated carrier doping levels n with reported carrier concentrations indicated at 300 K. (c) T-dependences of electron relaxation times τel. (d) T-dependences of the reciprocal
[image:4.595.313.542.67.233.2]materials had high ZeT at high n. Although there was a large
uncertainty because of the band-gap calculations, these find-ings can be used to accelerate experimental searches for new thermoelectric materials because they identify compounds with ZeT less than the target ZT. By combining calculation
results with experimental thermoelectric properties, we suc-cessfully estimated the T-dependence of τel for bulk
thermo-electric materials. This analysis can be used to investigate the quantitative effects of various scattering factors on the elec-tron and phonon systems.
Acknowledgments
This work was financially supported by a Ministry of Edu-cation, Culture, Sports, Science and Technology/Japan Soci-ety for the Promotion of Science grant-in-aid 23760647 and the Japan Science and Technology Agency MI2I (Materials
Research by Information Integration Initiative) program.
REFERENCES
1) A. F. Ioffe: Semiconductor Thermoelements and Thermoelectric
Cool-ing, (Infosearch, London, 1957).
2) D. M. Rowe: CRC Handbook of Thermoelectrics, (CRC Press, Boca Raton, 2010).
3) M.S. Dresselhaus, G. Dresselhaus, X. Sun, Z. Zhang, S.B. Cronin and T. Koga: Phys. Solid State 41 (1999) 679–682.
4) L.D. Hicks and M.S. Dresselhaus: Phys. Rev. B 47 (1993) 12727. 5) G.S. Nolas, G.A. Slack and S.B. Schujman: Semicond. Semimet. 69
(2000) 255–300.
6) K. Kuroki and R. Arita: J. Phys. Soc. Jpn. 76 (2007).
7) N. W. Ashcroft and D. Mermin: Introduction to Solid State Physics, (Saunders, Philadelphia, 1976).
8) J. M. Ziman: Electrons and Phonons: The Theory of Transport
Phe-nomena in Solids, (Clarendon Press, Oxford, 2001).
9) G.D. Mahan and J.O. Sofo: Proc. Natl. Acad. Sci. USA 93 (1996) 7436–7439.
10) Z. Fan, H.Q. Wang and J.C. Zheng: J. Appl. Phys. 109 (2011) 073713. 11) T. Takeuchi: Trans. JIM 50 (2009) 2359–2365.
12) T.J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J.V. Badding and J.O. Sofo: Phys. Rev. B 68 (2003) 125210.
13) C. Bera, M. Soulier, C. Navone, G. Roux, J. Simon, S. Volz and N. Mingo: J. Appl. Phys. 108 (2010) 124306.
14) S. Ahmad and S.D. Mahanti: Phys. Rev. B 81 (2010) 165203. 15) K. Kutorasiński, J. Tobola and S. Kaprzyk: Phys. Rev. B 87 (2013)
195205.
16) C. Stiewe, L. Bertini, M. Toprak, M. Christensen, D. Platzek, S. Wil-liams, C. Gatti, E. Müller, B.B. Iversen, M. Muhammed and M. Rowe: J. Appl. Phys. 97 (2005) 044317.
17) A.A. Snarskii, M.I. Zhenirovskii and I.V. Bezsudnov: Semiconductors 42 (2008) 80–85.
18) Inorganic Crystal Structure Database, Fachinformazion Karlsruhe, Germany.
19) P. Blaha, K. Schwarz, G.K.H. Madsen, D. Kvasnicka and J. Luitz:
WIEN2k. An augmented plane wave plus local orbitals program for calculating crystal properties (Vienna Univ. of Technology, Austria, 2001)
20) J.P. Perdew, K. Burke and M. Ernzerhof: Phys. Rev. Lett. 77 (1996) 3865–3868.
21) F. Tran and P. Blaha: Phys. Rev. Lett. 102 (2009) 226401.
22) G.K.H. Madsen and D.J. Singh: Comput. Phys. Commun. 175 (2006) 67.
23) Y. Katsura: J. Thermoelectric Soc. Jpn. 11 (2014) 19. 24) G.J. Snyder and E.S. Toberer: Nat. Mater. 7 (2008) 105. 25) G.D. Mahan: Solid State Phys. 51 (1998) 81.
26) K. Koumoto, I. Terasaki and R. Funahashi: MRS Bull. 31 (2006) 206– 210.
27) C.B. Vining, W. Laskow, J.O. Hanson, R. van der Beck and P.D. Gor-such: J. Appl. Phys. 69 (1991) 4333.
28) J.P. Dismukes, L. Ekstrom, E.F. Steigmeier, I. Kudman and D.S. Beers: J. Appl. Phys. 10 (1976) 2899.
29) V.I. Gatalskaya, E.M. Gololobov and L.A. Kurochkin: Phys. Status Solidi A 85 (1984) K51–K55.
30) K. van Benthem, C. Elsässer and R.H. French: J. Appl. Phys. 90 (2001) 6156.
31) D.C. Reynolds, D.C. Look and B. Jogai: Solid State Commun. 99 (1996) 873.
32) L.F. Mattheiss: Phys. Rev. B 43 (1991) 12549.
33) C.H. Olk, S.M. Yalisove and G.L. Doll: Phys. Rev. B 52 (1995) 1692. 34) T. Caillat, A. Borshchevsky and J.P. Fleurial: J. Appl. Phys. 80 (1996)
4442.
35) C. Persson and U. Lindefelt: Phys. Rev. B 54 (1996) 10257.
36) J.E. Mahan, A. Vantomme, G. Langouche and J.P. Becker: Phys. Rev. B 54 (1996) 16965.
37) L.D. Zhao, S.H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V.P. Dravid and M.G. Kanatzidis: Nature 508 (2014) 373.
38) P.V. Galiy, T.M. Nenchuk, O.R. Dveriy, A. Ciszewski, P. Mazur, S. Zu-ber and Y.M. Buzhuk: Chem. Met. Alloys 4 (2011) 1.
39) M.M. Ocker, F. Sharaf, H.M. Talaat, F. Metawe and M.A. El-Sherbiny: Solid State Commun. 76 (1990) 1293.
40) J. Horák, P. Lošťák, L. Koudelka and R. Novotný: Solid State Com-mun. 55 (1985) 1031.