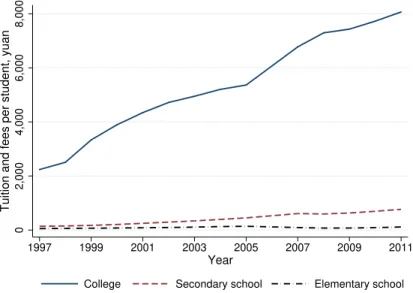
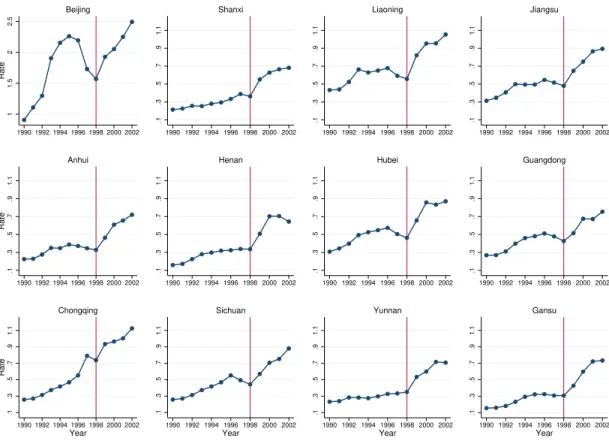
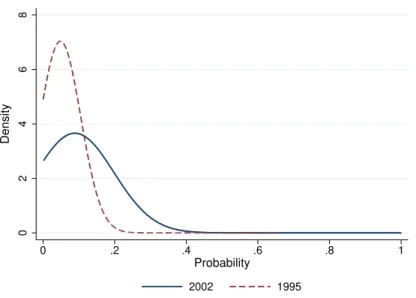
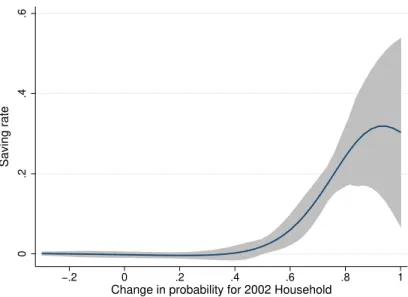
Three Essays on the Economics of Education Expansion
Full text
Figure

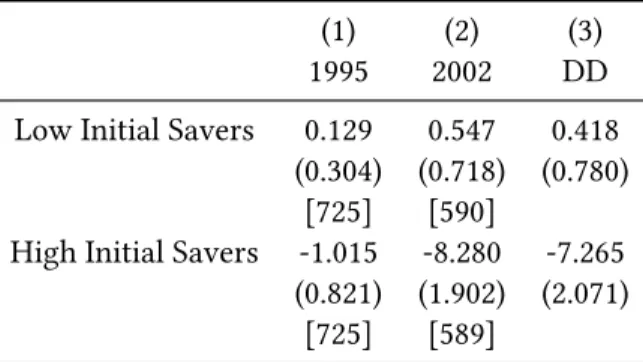
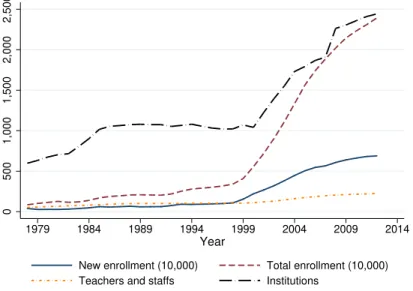
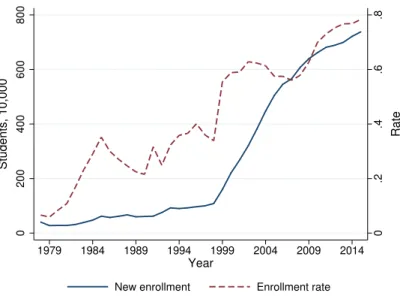
Related documents
By combining the technologies of the field proven and power dense AC laminated frame RPM AC motor with high performance permanent magnet (PM) salient pole rotor designs and
in a recent study of chemotherapy-naive patients with advanced or metastatic NSCLC treated with gefitinib in East Asia, the overall response rate and dis- ease stabilization rate
Notably, by combining our RNA-seq and AGO2-RIP-seq data we identified 144 and 161 genes whose binding onto AGO2 increased and decreased respectively in response to DNA damage in
Title Asymptotic distribution of the distance-based classifier under a strongly spiked eigenvalue model (Bayes Inference and Its Related Topics).. Author(s)
Relative house prices are a function of relative incomes, the relative household numbers to housing stock ratio, an interest rate to reflect the bigger effect of interest rates in
This paper concentrates on rating the current situation and future trends of solid biomass fuel trade and forest wood potential in Europe and fuel supply chains.. The annual
Chair, Search Committee, Department of Global, International, and Area Studies, University of North Carolina at Charlotte, 2012-2013. Member, Executive Committee, Department of
Di dalam pembelajaran, peserta didik didorong untuk menemukan sendiri dan mentransformasikan informasi kompleks, mengecek informasi baru dengan yang sudah ada dalam ingatannya,