2019 International Conference on Computation and Information Sciences (ICCIS 2019) ISBN: 978-1-60595-644-2
Calculation on External Heat Flux of a
Space Camera
Lian Xue, Jiaqi Liu, Lu Gao, Zhiqi Liu and Luping Zhang
ABSTRACT
In order to obtain accurate external heat flux data, the space system thermal simulation module in NX is used to solve the thermal analysis design problem on a camera in space flight section. The effects of different time, different seasons and different orbital altitude on the external heat flux of spacecraft surface are analyzed. The calculation results show that for different seasons and different orbital altitudes, the variation laws of external heat flux on the same surface are basically the same, and there are only differences in value. The differences are small, within 10 %; For the camera launched at different times of the day, the law of external heat flux changes is completely different, and difference in value is also very large. The heat flux in the area exposed to the sun is 6.38 times that of the heat flux in the shadow area. The results can be used to guide thermal design and calculate the temperature distribution of the camera. On the other hand, they provide reference for the design of other types of spacecraft with similar orbits.
Lian Xue, China National Key Laboratory of Science and Technology on Test Physics & Numerical Mathematics, Beijing, 100076, China;
Jiaqi Liu, China National Key Laboratory of Science and Technology on Test Physics & Numerical Mathematics, Beijing, 100076, China;
Lu Gao, China National Key Laboratory of Science and Technology on Test Physics & Numerical Mathematics, Beijing, 100076, China;
Zhiqi Liu, China National Key Laboratory of Science and Technology on Test Physics & Numerical Mathematics, Beijing, 100076, China;
1. INTRODUCTION
Spacecraft in orbit state will receive space external heat flux, which is an important factor affecting its temperature level. Therefore, prior to thermal analysis and thermal design work, the analysis of the external heat flux of the spacecraft is essential. The influencing factors of the external heat flux mainly include the orbital parameters, the position of the spacecraft in orbit, and the attitude of the spacecraft [1-3].
inclined orbiting satellite with the illumination angle and the intensity of the solar radiation, and analyzed the influence of the calculation time unit on the accuracy of the analytical model. When the satellite orbit altitude and the orbital dip are different, the extreme external The law of change of heat flux.
The above studies on external heat flux are mainly for spatially intact orbitals, while there are few studies on external heat flux for some orbitals. The camera studied in this paper is released by spacecraft in space, inertial flight for a period of time, and its spatial inertial flight trajectory basically conforms to the conditions of some satellite orbits. In this paper, the camera's space inertial flight trajectory is converted into six satellite numbers, and then the space system thermal simulation module in NX is used to calculate the camera's external heat flux, and the different days, seasons and different orbit altitudes of the same day are compared and analyzed. External heat flux. Provides a reference for further thermal analysis and thermal design work.
2. BASIC ASSUMPTIONS AND COMPUTATIONAL THEORIES
2.1 Basic Assumption
To simplify the calculation, the following assumptions are made for the model: (1)The camera is released from spacecraft by space, and relies on its inertial flight to meet the conditions of the satellite orbit;
(2)The camera attitude is three-axis stable to ground orientation, the flight direction is defined as +X direction, the ground direction is +Z, and the Y direction is determined according to the right-hand rule. The structure and coordinates are shown in Figure 1.
[image:3.612.191.404.524.637.2](3)The occlusion of the camera by other external devices is not considered.
TABLE I. CODE LEVEL SCHEME OF EXPERIMENTAL DESIGN.
Code level Soil relative water content (W, %FC)
Nitrogen application (N, g/plant-1)
Phosphorus (P2O5)
application (P, g/plant-1)
-1.682 30 0 0
-1 40 1 0.5
0 55 2.5 1.25
1 70 4 2
1.682 80 5 2.5
2.2 Theory of Computation
The calculation of the external heat flux of low-orbit satellites mainly includes three types: solar radiation, earth albedo radiation and earth infrared radiation:
(1) Sun radiation external heat flux
For the range of Earth's orbits in which the target camera is studied, sunlight can be thought of as a uniform, parallel beam with a solar constant S. On any micro-element area dA of the camera surface, the arriving solar radiation external heat fluxdq1 is:
1 cos s
dq S dA (1)
Where βs is the angle between the solar light vector and the normal surface of
the micro-element.
(2) Earthshine external heat flux
The orbit of the camera is still affected by the Earth's reflection of sunlight. Assuming that the earth is a diffuser, the reflection of sunlight obeys the Lambert cosine theorem, and the reflectivity is taken as a constant, then the external heat fluxdq2 of the earth reached by the surface dA of any micro-camera of the camera is:
'
1 2
2 2
cos cos cos
E
E A
dq SdA dA
l
Where η is the angle between the solar light vector and the normal surface of
the earth surface micro-element, α1is the angle between the surface micro-element
of the earth surface micro-element and the surface micro-element, and α2 is the
target micro-element surface method. The angle of the same surface micro-element is connected to the target micro-element.
(3) Earth infrared external heat flux
The earth is basically in thermal equilibrium in orbit. In the calculation of its orbital external heat flux, the earth can be assumed to be a uniform thermal equilibrium. The external infrared heat fluxdq3 of the outer surface of the camera, dA, is: ' 1 2 3 2 cos cos E E E A
dq dA dA
l
(3)Where E is the infrared radiation force of the earth's surface.
3. CALCULATION RESULTS AND ANALYSIS
In order to compare and analyze the external heat flux in the camera's flight motion, the motion trajectory is set to the same trajectory, that is, the same launch position, the flight speed and direction are the same, and the flight time is the same. The external heat flux after the camera is lifted is mainly affected by the time (early, middle, late), season (spring, summer, autumn and winter) and orbit altitude. Therefore, the external heat flux analysis mainly comes from three aspects: different time, different seasons and different orbit altitude. Compare and analyze.
This paper uses the flight start time 2018-9-22 12:00 and the orbital radius R=6800km as the benchmark to study different times (8 am, 12 noon, 8 pm, 1:00 am), different seasons (March) 22nd (spring), June 22nd (summer), September 22nd (autumn), December 22nd (winter) and different orbital radii (6800km, 7000km, 7200km, or orbit altitude are 421.863km, 621.863 respectively) Km, 821.863km) The external heat flux of the camera covers the external heat flux in all cases of the same motion trajectory.
3.1 The Influence of Different Times
Assume that the camera flight start time is Beijing time 2018-9-22 8:00, 2018-9-22 12:00, 2018-9-22 20:00 and 2018-9-23 1:00, corresponding GMT time They are 2018-9-22 0:00, 2018-9-22 4:00, 2018-9-22 12:00 and 2018-9-22 17:00,
and the coordinates of the star point at the start of flight are 30° north latitude. ,
120° east longitude, flying westward, flying at 8km/s and flying time is 20
Figure 2. Schematic diagram of motion trajectory.
The relationship between camera trajectory and shadow sunshine can be shown in figure 3 below.
(a)Flight start time8:00 (b)Flight start time12:00
(c)Flight start time20:00 (d)Flight start time1:00
Figure 3. Relationship between motion trajectory and shadow sunshine.
[image:6.612.188.410.374.589.2]Yangzhao District. When it was free to fly at 12:00 noon, it was completely in Yangzhao. District, when flying freely at 20:00 at night, it is entered into the Yangzhao District from the shadow area, and is completely in the shadow area at 1:00 am.
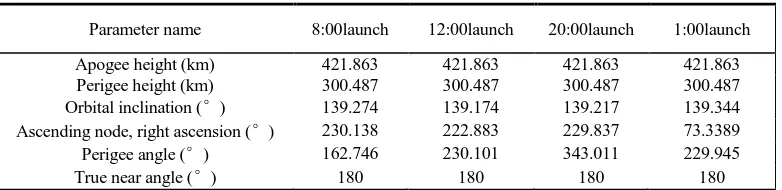
After converting the motion trajectory into a satellite orbit, the orbital parameters
can be obtained as shown in Table II. It can be seen from the table of the rising of
the orbit of the red meridians of the rising intersection point, which can Be considered to be three tracks rotating at different angles around the Z axis of the geocentric inertial coordinate system.
TABLE II. CONVERTED SATELLITE ORBITAL PARAMETERS (AT DIFFERENT TIMES).
Parameter name 8:00launch 12:00launch 20:00launch 1:00launch
Apogee height (km) 421.863 421.863 421.863 421.863 Perigee height (km) 300.487 300.487 300.487 300.487 Orbital inclination (°) 139.274 139.174 139.217 139.344 Ascending node, right ascension (°) 230.138 222.883 229.837 73.3389 Perigee angle (°) 162.746 230.101 343.011 229.945 True near angle (°) 180 180 180 180
The surface of each camera at different starting flight moments reaches the total external heat flux (sum of direct sunlight, earth reflection and earth red external heat flux) as shown in Figure 4.
[image:7.612.104.495.268.363.2](c).Flight start time 20:00 (d).Flight start time 1:00
Figure 4. The surface of the camera in flight reaches the external heat flux (different starting flight time).
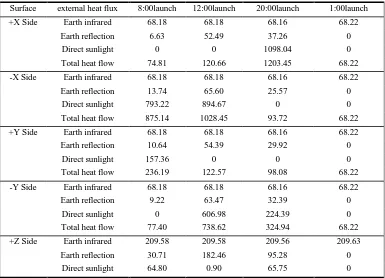
Table III calculates the average external heat flux received by each surface in
20min, in which the total is the sum of the external heat flux received by all faces.
TABLE III. STATISTICS OF ARRIVAL EXTERNAL HEAT FLUX MEAN OF EACH SIDE AT THREE DIFFERENT TIMES (W/m2).
Surface external heat flux 8:00launch 12:00launch 20:00launch 1:00launch +X Side Earth infrared 68.18 68.18 68.16 68.22
Earth reflection 6.63 52.49 37.26 0 Direct sunlight 0 0 1098.04 0 Total heat flow 74.81 120.66 1203.45 68.22
-X Side Earth infrared 68.18 68.18 68.16 68.22 Earth reflection 13.74 65.60 25.57 0
Direct sunlight 793.22 894.67 0 0 Total heat flow 875.14 1028.45 93.72 68.22
+Y Side Earth infrared 68.18 68.18 68.16 68.22 Earth reflection 10.64 54.39 29.92 0
Direct sunlight 157.36 0 0 0 Total heat flow 236.19 122.57 98.08 68.22
-Y Side Earth infrared 68.18 68.18 68.16 68.22 Earth reflection 9.22 63.47 32.39 0
Direct sunlight 0 606.98 224.39 0 Total heat flow 77.40 738.62 324.94 68.22 +Z Side Earth infrared 209.58 209.58 209.56 209.63
[image:8.612.105.490.407.685.2]Total heat flow 305.09 392.94 370.59 209.63 -Z Side Earth infrared 0 0 0 0
Earth reflection 0 0 0 0 Direct sunlight 112.35 677.45 350.11 0 Total heat flow 112.35 677.45 350.11 0 Total Earth infrared 482.30 482.29 482.18 482.53
Earth reflection 70.95 418.42 220.42 0 Direct sunlight 1127.73 2179.99 1738.29 0 Total heat flow 1680.98 3080.70 2440.89 482.53
It can be seen from Table III that the ±X surface and the ±Y plane are
identical to the Earth's red external heat flux because the four faces are perpendicular to the Earth's surface. +Z is facing the earth, the red heat of the earth is the largest, and the -Z is back to the earth. The earth's red external heat flux is zero. The +X plane and the -X plane, the +Y plane and the -Y plane, and the opposite faces of the +Z plane and the -Z plane are not directly irradiated by the sun. Therefore, the direct heat flow of the sun is 0, one side has a value, and - The Z plane faces away from the Earth and is only exposed to direct sunlight. The Earth's infrared and Earth's reflections are both zero.
From the total results, it can be seen that the camera that started flying at noon is completely in the positive area, and the maximum impact due to external heat flux is 3080.7W/2, which is larger than the external heat flux of the starting camera at 8:00 in the morning. 45.4%, which is 20.8% larger than the heat flow of the starting camera at 20:00, which is 6.38 times of the heat flow of the starting camera at 1:00 am (complete shadow).
3.2 Effects of Different Seasons
Assume that the coordinates of the star point at the beginning of the camera are
the same, which is 30° north latitude and 120° east longitude. The starting flight
times are Beijing 22nd, 2018 12:00, June 22nd, 2018 12:00, September 22nd, 2018 12 :00 and December 22nd, 2018 12:00, flying west, flying at 8km/s and flying for
Table IV. CONVERTED SATELLITE ORBIT PARAMETERS (DIFFERENT SEASONS).
Parameter name 3-22launch 6-22launch 9-22launch 12-22launch Apogee height (km) 421.863 421.863 421.863 421.863 Perigee height (km) 300.487 300.487 300.487 300.487 Orbital inclination (°) 139.313 139.319 139.174 139.17 Ascending node, right ascension (°) 41.3581 132.201 222.883 312.405
Perigee angle (°) 229.874 230.094 230.101 229.878 True near angle (°) 180 180 180 180
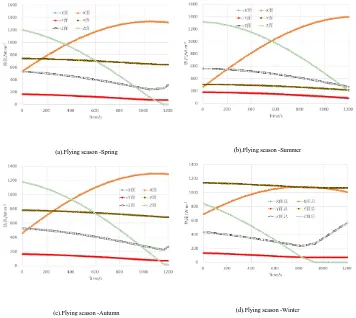
Cameras flying in four different seasons arrive at the total external heat flux as shown in Figure 5.
(a).Flying season -Spring (b).Flying season -Summer
(c).Flying season -Autumn (d).Flying season -Winter
[image:10.612.120.476.302.620.2]Table V shows the average external heat flux of each surface in 20 min, where the sum is the sum of the external heat flux of all the faces.
Table V. Average statistics of external heat flux reached on each side of the four seasons(W/m2).
Surface External heat flux Spring Summer Autumn Winter +X Side Earth infrared 68.18 68.18 68.18 68.18 Earth reflection 50.29 71.24 52.49 24.81 Direct sunlight 0 0 0 0 Total heat flow 118.47 139.41 120.66 92.98 -X Side Earth infrared 68.18 68.18 68.18 68.18 Earth reflection 63.85 84.03 65.60 34.52 Direct sunlight 961.20 825.13 894.67 880.77 Total heat flow 1093.22 977.33 1028.45 983.46 +Y Side Earth infrared 68.18 68.18 68.18 68.18
Earth reflection 52.81 76.64 54.39 23.94 Direct sunlight 0 0 0 0 Total heat flow 120.99 144.81 122.57 92.12 -Y Side Earth infrared 68.18 68.18 68.18 68.18 Earth reflection 61.04 78.58 63.47 35.38 Direct sunlight 566.88 124.62 606.98 993.05 Total heat flow 696.10 271.38 738.62 1096.60 +Z Side Earth infrared 209.58 209.58 209.58 209.58
Earth reflection 176.29 240.36 182.46 91.31 Direct sunlight 4.91 0 0.90 50.04 Total heat flow 390.78 449.94 392.94 350.94
-Z Side Earth infrared 0 0 0 0 Earth reflection 0 0 0 0 Direct sunlight 654.76 894.39 677.45 337.39 Total heat flow 654.76 894.39 677.45 337.39
Total Earth infrared 482.29 482.29 482.29 482.29 Earth reflection 404.28 550.84 418.42 209.96 Direct sunlight 2187.75 1844.13 2179.99 2261.25 Total heat flow 3074.32 2877.26 3080.70 2953.50
It can be seen from Table V that in the four seasons of the camera, the heat flow
on the same surface differs only in numerical value, but the basic laws are exactly the same, and the type and variation law of the external heat flux are the same.
[image:11.612.115.479.170.573.2]3.3 Effects of Different Orbit Altitude
Assume that the camera's Flight start time is the same as Beijing time 2018-9-22
12:00, Flight start time is the same as the coordinates of the star point, which is 30°
north latitude and 120° east longitude. It flies westward, only the orbit altitude is
[image:12.612.138.457.232.312.2]different, respectively R=6800km At 7000km and 7200km, the flight speed is 8km/s and the flight time is 20 minutes. The converted satellite orbit parameters are shown in Table VI.
Table VI. Converted satellite orbital parameters (different orbit altitude).
Parameter name R=6800km R=7000km R=7200km Apogee height (km) 421.863 866.692 1472.29 Perigee height (km) 300.487 621.863 821.863 Orbital inclination (°) 139.174 139.145 139.115 Ascending node, right ascension (°) 222.883 222.829 222.774 Perigee angle (°) 230.101 50.0603 50.0193 True near angle (°) 180 0 0
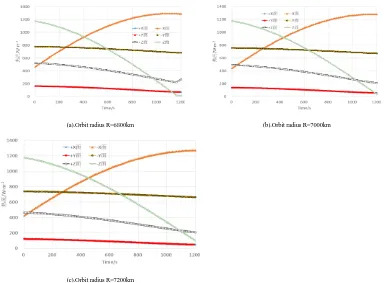
[image:12.612.106.490.372.655.2]Different orbit altitude cameras arrive at the total external heat flux as shown in Figure 6.
(a).Orbit radius R=6800km (b).Orbit radius R=7000km
(c).Orbit radius R=7200km
Table VII shows the average external heat flux of each face within 20 min of different orbit altitudes, where the sum is the sum of the external heat flux of all faces.
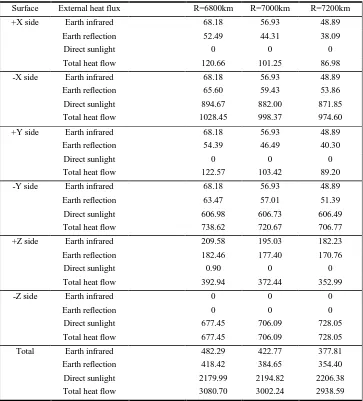
Table VII. Average statistics of external heat flux from different orbit altitudes (W/m2).
Surface External heat flux R=6800km R=7000km R=7200km
+X side Earth infrared 68.18 56.93 48.89 Earth reflection 52.49 44.31 38.09
Direct sunlight 0 0 0 Total heat flow 120.66 101.25 86.98
-X side Earth infrared 68.18 56.93 48.89 Earth reflection 65.60 59.43 53.86 Direct sunlight 894.67 882.00 871.85 Total heat flow 1028.45 998.37 974.60 +Y side Earth infrared 68.18 56.93 48.89
Earth reflection 54.39 46.49 40.30 Direct sunlight 0 0 0 Total heat flow 122.57 103.42 89.20 -Y side Earth infrared 68.18 56.93 48.89 Earth reflection 63.47 57.01 51.39 Direct sunlight 606.98 606.73 606.49 Total heat flow 738.62 720.67 706.77 +Z side Earth infrared 209.58 195.03 182.23 Earth reflection 182.46 177.40 170.76
Direct sunlight 0.90 0 0 Total heat flow 392.94 372.44 352.99 -Z side Earth infrared 0 0 0
It can be seen from Table VII that for different orbit altitude cameras, the heat flux on the same surface differs only in numerical values, but the basic laws are exactly the same, and the type and variation law of the external heat flux are the same.
It can be seen from the total results that the external heat flux of the camera is basically the same under different orbit altitudes, and the deviation is within 5%.
4. CONCLUSIONS
Combining the above calculation results of external heat flux, the space camera of the same Flight start time, whether it is different seasons or different orbit altitude, the same surface is subject to the same change of external heat flux, only the numerical value is different, and the difference is small. Within 10% of the cameras that started flying at different times of the day, the variation law of external heat flux is completely different, and the numerical difference is also very large. The heat flow in the positive area is 6.38 times that of the heat flow in the shadow area. The results can be used to guide further thermal analysis and thermal design work of a space camera, and to provide reference for the design of other types of spacecraft of similar orbits.
REFERENCES
1. Guirong Min. 1991. “Satellite Thermal Control Technology,” Beijing: China Aerospace
Publishing House, 1991.
2. Donabedian M. 2002. “Spacecraft Thermal Control Handbook,” Volume II: Cryogenics. 2002. 3. Zengqi Hou, Jingang Hu. 2007. “Spacecraft Thermal Control Technology,” Beijing: China
Science and Technology Press, 2007.
4. Oneill R. 2013. “Thermal control design analysis of an on-orbit assembly spacecraft,”
Conference on Advanced Technology for Future Space Systems. 2013.
5. Oneill R, Lorentz D. 2013. “A vector approach to numerical computation of view factors and application to space heating,” Aerospace Sciences Meeting. 2013.
6. Taylor R P, Luck R. 1995. “Comparison of reciprocity and closure enforcement methods for radiation view factors,” Journal of Thermo physics and Heat Transfer, 1995, 9(4): 660-666. 7. Campbell P M. 1967. “Monte Carlo method for radiative transfer,” International Journal of Heat
& Mass Transfer, 1967, 10(4): 519-527.
8. Gray D, Davies F. Blanchard K.A. 1967. “Monte Carlo simulation of spacecraft manufacturing, assembly, and sterilization.” 1967.
9. Baturkin V. 2005. “Micro-satellites thermal control—concepts and components,” Acta
Astronautica, 2005, 56(1-2): 161-170.
10. Khaniki H B. 2014.Hossein Karimian S M. “Determining the heat flux absorbed by satellite surfaces with temperature data,” Journal of Mechanical Science and Technology, 2014, 28(6): 2393-2398.
12. Xianwen Ning, Jiaxun Zhang, Hai Jiang, et al. 2008. “Analytical model of extreme external heat flux for inclined orbital hexahedron satellites,” Journal of Astronautics, 2008, 29(3): 754-759. 13. Yupeng Zhou, Xin Zhao, Tengfei Sun, et al. 2013. “Analysis of the variation law of external heat
flux in a fixed-point observation mode of astronomical exploration satellites,” Spacecraft
Engineering, 2013, 22(4): 49-55.
14. Richa Hu, Liang Guo, Chunlong Liu. 2015. “Calculation of external heat flux for atypical circular orbit space optical remote sensor,” Computer Simulation, 2015(7): 60-64.