OBSERVATION ON THE POSITIVE PELL EQUATION

Observation on the Positive Pell Equation

y

2



2

x

2



18

M.A.Gopalan

1

and Sharadha Kumar

2

1_{Professor, Department of Mathematics, SIGC, Trichy, Tamilnadu, India. Email: mayilgopalan@gmail.com} 2_{M.Phil Scholar, Department of Mathematics, SIGC, Trichy, Tamilnadu, India. Email: sharadhak12@gmail.com}

Article Received: 04 October 2017 Article Accepted: 23 November 2017 Article Published: 12 December 2017

1. INTRODUCTION

The binary quadratic Diophantine equations of the form

ax

2



by

2



N

,



a

,

b

,

N



0



are rich in variety and have

been analyzed by many Mathematicians for their respective integer solutions for particular values of a, andb N .

In this context, one may refer [1-13]. This communication concerns with the problem of obtaining non-zero distinct

integer solutions to the binary quadratic equation given by

y

2



2

x

2



18

representing hyperbola. A few

interesting relations among its solutions are presented. Knowing an integral solution of the given hyperbola, integer

solutions for other choices of hyperbolas and parabolas are presented. Also, employing the solutions of the given

equation, special Pythagorean triangle is constructed.

2. METHOD OF ANALYSIS

The binary quadratic equation representing hyperbola is given by

18

2

2 2

_

_x

_

y

(1)

The smallest positive integer solution

(

x

₀

,

y

₀

)

of (1) is

6

,

3

₀ 0



y



x

To obtain, the other solutions of (1), consider the pellian equation

1

2

2 2

_

_x

_

y

₍₂₎

Whose smallest positive integer solution is

3 ~ , 2 ~

0 0  y  x

The general solution

(

~

x

_n

,

~

y

_n

)

of (2) is given by



3

2

2



,

0

,

1

,

2

....

~

2

~

_y

_

_x

_

_

n1

_n

_

n

n (3)

A B S T R A C T

The hyperbola represented by the binary quadratic equation

y

2



2

x

2



18

is analyzed for finding its non-zero distinct integer solutions. A few interesting relations among its solutions are presented. Also, knowing an integral solution of the given hyperbola, integer solutions for other choices of hyperbolas and parabolas are presented. Also, employing the solutions of the given equation, special Pythagorean triangle is constructed.



3

2

2



,

0

,

1

,

2

....

~

2

~

_y

_

_x

_

_

n1

_n

_

n

n (4)

From (3) and (4), solving for

y

~

_n

,

~

x

_n, we have









n

n n

n f

y

2 1 2

2 3 2

2 3 2 1

~ 1 1

   

 _{  }

  









n

n n

n

g

x

2

2

1

2

2

3

2

2

3

2

2

1

~

1 1

_









_

_

_



 

Applying Brahmagupta lemma between the solutions

(

x

₀

,

y

₀

)

and

(

~

x

_n

,

~

y

_n

)

, the general solution

(

x

_n1

,

y

_n1

)

is

n n

n x y y x

x _1 ₀~  ₀~

n n

n y y x x

y _1 ₀~ 2 ₀~

n n

n

f

g

x

2

3

2

3

1







_ (5)

n n

n

f

g

y

2

2

6

2

6

1





 (6)

Thus, (5) and (6) represent the integer solutions of the hyperbola (1).

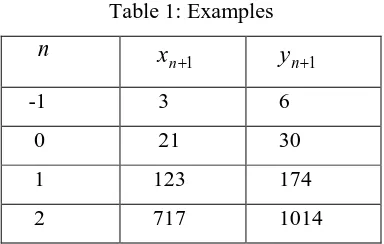
A few numerical examples are given in the following table 1

Table 1: Examples

n

1

 n

x

y

_n1 -1 3 6

0 21 30

1 123 174

2 717 1014

Note that the

x



values are odd and yvalues are even.

Also, x_n1 0



mod3



, y_n10



mod6



Recurrence relations for

x

and y are:

...

1

,

0

,

1

,

0

6

_{2 1}

3

















x

x

n

x

_{n n n}

...

1

,

0

,

1

,

0

6

_{2 1}

3

















y

y

n

1. A few interesting relations among the solutions are given below



x

_n2



3

x

_n1



2

y

_n1



0



3

x

_n2



x

_n1



2

y

_n2



0



17

x

_n2



3

x

_n1



2

y

_n3



0



12

y

_n1



17

x

_n1



x

_n3



0



3

y

_n1



4

x

_n1



y

_n2



0



17

y

_n1



24

x

_n1



y

_n3



0



4

y

_n2



x

_n1



x

_n3



0



y

_n2



4

x

_n1



3

y

_n1



0



17

y

_n2



4

x

_n1



3

y

_n3



0



2

y

_n3



3

x

_n1



17

x

_n2



0



12

y

_n3



x

_n1



17

x

_n3



0



3

x

_n3



17

x

_n2



2

y

_n1



0



x

_n3



3

x

_n2



2

y

_n2



0



3

x

_n3



x

_n2



2

y

_n3



0



y

_n1



4

x

_n2



3

y

_n2



0



y

_n1



8

x

_n2



y

_n3



0



3

y

_n1



4

x

_n3



17

y

_n2



0



3

y

_n2



4

x

_n2



y

_n3



0



y

_n2



4

x

_n3



3

y

_n3



0



y

_n1



24

x

_n3



17

y

_n3



0



y

_n3



3

y

_n2



4

x

_n2



0



3

y

_n3



17

y

_n2



4

x

_n1



0

2. Each of the following expressions represents a cubical integer







12 _{3 4} 60 _{3 3}

 

312 ₂ 60 ₁





36 1

 



  n  n  n

n x x x

x







12 _{3 5} 348 _{3 3}

 

312 ₃ 348 ₁





216 1

 



  n  n  n

n x x x







2 _{3 3} 2 _{3 3}

 

32 ₁ 2 ₁





3 1   

  n  n  n

n x y x

y







12 _{3 4} 84 _{3 3}

 

312 ₂ 84 ₁





54 1

 



  n  n  n

n x y x

y







12 _{3 5} 492 _{3 3}

 

312 ₃ 492 ₁





306 1

 



  n  n  n

n x y x

y







60 _{3 5} 348 _{3 4}

 

360 ₃ 348 ₂





36 1

 



  n  n  n

n x x x

x







60 _{3 3} 12 _{3 4}

 

360 ₁ 12 ₂





54 1

 



  n  n  n

n x y x

y







60 _{3 4} 84 _{3 4}

 

360 ₂ 84 ₂





18 1

 



  n  n  n

n x y x

y







60 _{3 5} 492 _{3 4}

 

360 ₃ 492 ₂





54 1

 



  n  n  n

n x y x

y







348 _{3 3} 12 _{3 5}

 

3348 ₁ 12 ₃





306 1

 



  n  n  n

n x y x

y







348 _{3 4} 84 _{3 5}

 

3348 ₂ 84 ₃





54 1

 



  n  n  n

n x y x

y







348 _{3 5} 492 _{3 5}

 

3348 ₃ 492 ₃





18 1

 



  n  n  n

n x y x

y







84 _{3 3} 12 _{3 4}

 

384 ₁ 12 ₂





72 1

 



  n  n  n

n y y y

y







492 _{3 3} 12 _{3 5}

 

3492 ₁ 12 ₃





432 1

 



  n  n  n

n y y y

y







492 _{3 4} 84 _{3 5}

 

3492 ₂ 84 ₃





72 1

 



  n  n  n

n y y y

y

3. Each of the following expressions represents bi-quadratic integer







432

2160

 

4

12

60



2592



36

1

₂ 1 2 4 4 5 4

2

x

n



x

n



x

n



x

n









2592

75168

 

4

12

348



93312



216

1

2 1 3 4 4 6 4

2

x

n



x

n



x

n



x

n









6

6

 

4

2

2



18



3

1

₂ 1 1 4 4 4 4

2

y

n



x

n



y

n



x

n









648

4536

 

4

12

84



5832



54

1

2 1 2 4 4 5 4







3672

150552

 

4

12

492



187272



306

1

2 1 3 4 4 6 4

2

y

n



x

n



y

n



x

n









2160

12528

 

4

60

348



2592



36

1

2 2 3 5 4 6 4

2

x

n



x

n



x

n



x

n









3240

648

 

4

60

12



5832



54

1

₂ 2 1 5 4 4 4

2

y

n



x

n



y

n



x

n









1080

1512

 

4

60

84



648



18

1

2 2 2 5 4 5 4

2

y

n



x

n



y

n



x

n









3240

26568

 

4

60

492



5832



54

1

2 2 3 5 4 6 4

2

y

n



x

n



y

n



x

n









106488

3672

 

4

348

12



187272



306

1

₂ 3 1 6 4 4 4

2

y

n



x

n



y

n



x

n









18792

4536

 

4

348

84



5832



54

1

2 3 2 6 4 5 4

2

y

n



x

n



y

n



x

n









6264

8856

 

4

348

492



648



18

1

2 3 3 6 4 6 4

2

y

n



x

n



y

n



x

n









6048

864

 

4

84

12



10368



72

1

2 2 1 5 4 4 4

2

y

n



y

n



y

n



y

n









212544

5184

 

4

492

12



373248



432

1

2 3 1 6 4 4 4

2

y

n



y

n



y

n



y

n







 





35424

6048

4

492

84

10368



72

1

₂ 3 2 6 4 5 4

2

y

n



y

n



y

n



y

n



4. Each of the following expressions represents Nasty number





432 72 _{2 3} 360 _{2 2}



36 1

  

 x _n x _n





2592 72 _{2 4} 2088 _{2 2}



216 1

  

 x _n x _n





36 12 _{2 2} 12 _{2 2}



3 1

  

 y _n x _n





648 72 _{2 3} 504 _{2 2}



54 1

  

 y _n x _n





3672 72 _{2 4} 2952 _{2 2}



306 1

  





432 360 _{2 4} 2088 _{2 3}



36

1

  

 x _n x _n





648 360 _{2 2} 72 _{2 3}



54 1

  

 y _n x _n





216 360 _{2 3} 504 _{2 3}



18 1

  

 y _n x _n





648 360 _{2 4} 2952 _{2 3}



54 1

  

 y _n x _n





3672 2088 _{2 2} 72 _{2 4}



306 1

  

 y _n x _n





648 2088 _{2 3} 504 _{2 4}



54 1

  

 y _n x _n





216 2088 _{2 4} 2952 _{2 4}



18 1

  

 y _n x _n





864 504 _{2 2} 72 _{2 3}



72 1

  

 y _n y _n





5184 2952 _{2 2} 72 _{2 4}



432 1

  

 y _n y _n





864 2952 _{2 3} 504 _{2 4}



72 1

  

 y _n y _n

3. REMARKABLE OBSERVATIONS

3.1 Employing linear combinations among the solutions of (1), one may generate integer solutions for other choices of hyperbola which are presented in table 2 below

Table 2: Hyperbola

Sl.no Hyperbola



X

n

,

Y

n



1

10368

2

X

_n2



Y

_n2







12

x

n2



60

x

n1

 

,

84

x

n1



12

x

n2





2

373248

2

X

_n2



Y

_n2







12

x

n3



348

x

n1

 

,

492

x

n1



12

x

n3





3

72

2

X

_n2



Y

_n2







2

y

n1



2

x

n1

 

,

4

x

n1



2

y

n1





4

23328

2

X

_n2



Y

_n2







12

y

n2



84

x

n1

 

,

120

x

n1



12

y

n2





5

749088

2

X

_n2



Y

_n2







12

y

n3



492

x

n1

 

,

696

x

n1



12

y

n3





6

10368

7

23328

2

X

_n2



Y

_n2







60

y

n1



12

x

n2

 

,

24

x

n2



84

y

n1





8

2592

2

X

_n2



Y

_n2







60

y

n2



84

x

n2

 

,

120

x

n2



84

y

n2





9

23328

2

X

_n2



Y

_n2







60

y

n3



492

x

n2

 

,

696

x

n2



84

y

n3





10

749088

2

X

_n2



Y

_n2







348

y

n1



12

x

n3

 

,

24

x

n3



492

y

n1





11

23328

2

X

_n2



Y

_n2







348

y

n2



84

x

n3

 

,

120

x

n3



492

y

n2





12

2592

2

X

_n2



Y

_n2







348

y

n3



492

x

n3

 

,

696

x

n3



492

y

n3





13

41472

2

X

_n2



Y

_n2







84

y

n1



12

y

n2

 

,

24

y

n2



120

y

n1





14

1492992

2

X

_n2



Y

_n2







492

y

n1



12

y

n3

 

,

24

y

n3



696

y

n1





15

41472

2

X

_n2



Y

_n2







492

y

n2



84

y

n3

 

,

120

y

n3



696

y

n2





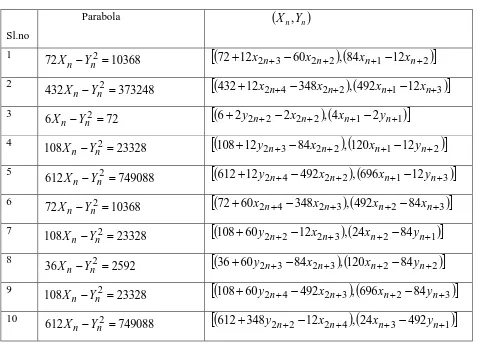
3.2 Employing linear combination among the solutions for other choices of parabola which are presented in table 3 below

Table 3: Parabola

Sl.no

Parabola



X

n

,

Y

n



1

10368

72

X

_n



Y

_n2







72



12

x

2n3



60

x

2n2

 

,

84

x

n1



12

x

n2





2

373248

432

X

_n



Y

_n2







432



12

x

2n4



348

x

2n2

 

,

492

x

n1



12

x

n3





3

72

6

X

_n



Y

_n2







6



2

y

2n2



2

x

2n2

 

,

4

x

n1



2

y

n1





4

23328

108

X

_n



Y

_n2







108



12

y

2n3



84

x

2n2

 

,

120

x

n1



12

y

n2





5

749088

612

X

_n



Y

_n2







612



12

y

2n4



492

x

2n2

 

,

696

x

n1



12

y

n3





6

10368

72

X

_n



Y

_n2







72



60

x

2n4



348

x

2n3

 

,

492

x

n2



84

x

n3





7

23328

108

X

_n



Y

_n2







108



60

y

2n2



12

x

2n3

 

,

24

x

n2



84

y

n1





8

2592

36

X

_n



Y

_n2







36



60

y

2n3



84

x

2n3

 

,

120

x

n2



84

y

n2





9

23328

108

X

_n



Y

_n2







108



60

y

2n4



492

x

2n3

 

,

696

x

n2



84

y

n3





10

749088

11

23328

108

X

_n



Y

_n2







108



348

y

2n3



84

x

2n4

 

,

120

x

n3



492

y

n2





12

2592

36

X

_n



Y

_n2







36



348

y

2n4



492

x

2n4

 

,

696

x

n3



492

y

n3





13

41472

144

X

_n



Y

_n2







144



84

y

2n2



12

y

2n3

 

,

24

y

n2



120

y

n1





14

1492992

864

X

_n



Y

_n2







864



492

y

2n2



12

y

2n4

 

,

24

y

n3



696

y

n1





15

41472

144

X

_n



Y

_n2







144



492

y

2n3



84

y

2n4

 

,

120

y

n3



696

y

n2





3.3 Let

p

,

q

be two non-zero distinct integers such that pq0.Treat

p

,

q

as the generators of the Pythagorean triangle T





,



,





Where





2

pq

,





p

2



q

2

,





p

2



q

2

,

p



q



0

Taking

p



x

n₁



y

n₁

,

q



x

n₁, it is observed that T





,



,





is satisfied by the following relations:

18

 











  

P A

4

1 1

2  x_n y_n P

A

Where A,P represent the area and perimeter of T





,



,





.

4. CONCLUSION

In this paper, we have presented infinitely many integer solutions for the Diophantine equation, represented by

hyperbola is given by

y

2



2

x

2



18

. As the binary quadratic Diophantine equations are rich in variety, one may

search for the other choices of equations and determine their integer solutions along with suitable properties.

REFERENCES

[1] L.E.Disckson, History of theory of Numbers, Vol.II, Chelsea Publishing co., New York (1952).

[2] L.J.Mordell, Diophantine Equations, Academic Press, London (1969).

[3] Gopalan et al., Integral points on the hyperbola



a



2



x

2



ay

2



4

a



k



1





2

k

2

,

a

,

k



0

, Indian

journal of science,1(2), 2012, 25-126.

[5] S.Vidhyalakshmi, et al., Observations on the hyperbola

ax

2





a



1



y

2



3

a



1

Discovery, 4(10), 2013,

22-24.

[6] K.Meena, S.Vidhyalakshmi, A.Nivetha, On the Binary Quadratic Diophantine Equation

0

14

4

2

2

_

_xy

_

_y

_

_x

_

x

, Sch.J.Phys.Math.Stat., Volume-3, Issue-1, 2016, Page no:15-19.

[7] K.Meena, S.vidhyalakshmi, R.Janani, On the Binary quadratic Diophantine Equation

0

21

9

2

2

_

_xy

_

_y

_

_x

_

x

, IJETER, Volume-4, Issue-7, 2016, Page no:1-4.

[8] K.Meena, MA.Gopalan, S.Nandhini, On the binary quadratic Diophantine equation

y

2



68

x

2



13

International Journal of Advanced Education and Research, Volume 2, Issue 1,2017, Page no.59-63.

[9] K.Meena, S.Vidhyalakshmi, R.Sobana Devi, On the binary quadratic equation

y

2



7

x

2



32

International

Journal of Advanced Science and Research, Volume 2, Issue 1, 2017, Page no.18-22 .

[10]K.Meena, MA.Gopalan, S.Hemalatha, On the hyperbola

y

2



8

x

2



16

National Journal of

Multidisciplinary Research and Developement, Volume 2, Issue 1, 2017, Page no.01-05.

[11]MA.Gopalan, KK.Viswanathan, G Ramya, On the Positive Pell equation

y

2



12

x

2



13

International

Journal of Advanced Education and Research, Volume 2, Issue 1, 2017, Page no.04-08.

[12]K.Meena, MA.Gopalan, V Sivaranjani, On the Positive Pell equation

y

2



102

x

2



33

International Journal

of Advanced Education and Research, Volume 2, Issue 1, 2017, Page no.91-96 .

[13]K.Meena, S.Vidhyalakshmi, N.Bhuvaneswari, On the binary quadratic Diophantine equation

24

10

2

2

_

_

x

y

International Journal of Multidisciplinary Education and Research, Volume 2, Issue 1, 2017,