Adjacent Vertex Distinguishing Total Coloring of Line and Splitting Graph of Some Graphs

(1)

ISSN: 2279-087X (P), 2279-0888(online) Published on 4 April 2017

www.researchmathsci.org

DOI: http://dx.doi.org/10.22457/apam.v13n2a3

173

Adjacent Vertex Distinguishing Total Coloring of Line

and Splitting Graph of Some Graphs

K.Thirusangu1 and R.Ezhilarasi2 1

Department of Mathematics, S.I.V.E.T College, Gowrivakkam Chennai - 600 073, India

2

Ramanujan Institute for Advanced Study in Mathematics University of Madras, Chennai - 600 005, India. 2

Corresponding author. Email: ezhilmath@gmail.com; ezhilarasi@unom.ac.in

Received 9 March 2017; accepted 28 March 2017

Abstract. In this paper, we prove the existence of the adjacent vertex distinguishing total coloring of line graph of Fan graph Fn, double star K1,n,n, Friendship graph

n

F and splitting graph of path Pn, cycle Cn, star K1,n and sun let graph

n

S2 in detail.

Keywords: simple graph, adjacent vertex distinguishing total coloring, line graph, splitting graph, path, cycle, star, sun let, fan, double star and friendship graph.

AMS Mathematics Subject Classification (2010): 05C15, 05C38, 05C76 1. Introduction

Throughout this paper, we consider finite, simple, connected and undirected graph ))

( ), ( (

= V G E G

G . For every vertex u,v∈V(G), the edge connecting two vertices is denoted by uv∈E(G). For all other standard concepts of graph theory, we see [1,2,5]. For graphs G1 and G2, we let G1∪G2 denotes their union, that is,

) ( ) ( = )

(G₁ G₂ V G₁ V G₂

V ∪ ∪ and E(G₁∪G₂)=E(G₁)∪E(G₂). If a simple graph G has two adjacent vertices of maximum degree, then

ψ

_avt(G)≥∆(G)+2. Otherwise, if a simple graph G does not have two adjacent vertices of maximum degree, then

1 ) ( = )

(G ∆ G +

avt

ψ

. The well-known

AVDTC

conjecture, made by Zhang et al. [8] says that every simple graph

G

has

χ

_avt(G)≤∆(G)+3. AVDTC of tensor product of graphs are discussed in litrature [6,7]. (2,1)-total labelling of cactus graphs and adjacent vertex distinguishing edge colouring of cactus graphs are discussed in literature [3,4]. Throughout the paper, we denote the path graph, cycle graph, complete graph, star graph, sun let, fan graph, double star and friendship graph by P_n, C_n, K_n, K_1,_n, S2n

, F_n,

n

(2)

174

any pair of adjacent vertices have distinct set of colors.

A total k-coloring of the graph G is adjacent vertex distinguishing, if a mapping f :V(G)∪E(G)→{1,2,⋯,k}, k∈_Z+ such that any two adjacent or incident elements in V(G)∪E(G) have different colors. The minimum number of colors required to give an adjacent vertex distinguishing total coloring (abbreviated as AVDTC) to the graph

G

is denoted by

χ

avt(G).

First, we find the adjacent vertex distinguishing total chromatic number of Fan graph, double star graph, Friendship graph and complete graph.

Proposition 1.1.

χ

_avt(F_n)=n+1, n>3.

Proof: Fan graph denoted by Fn, is a graph obtained by joining all vertices of the path n

P to a further vertex called the center vertex

v

. Thus Fn contains

n

+

1

vertices and

1

2 n

−

edges. Here, we have the vertex and edge set V(F_n)=

{

v,v₁,v₂,⋯,v_n

}

and

(

) (

)

{

1

}

1 1 = 1

= = ]

[ ∪ n− _i _i₊

i i n

i

n vv vv

F

E

∪

. Now we define f :V(F_n)∪E(F_n)→{1,2,⋯,k} given by,

1 = ) ( , 2

= ) ( 2 = ) ( 1, 1

1 = ) ( =

) ( , 1

1 1

− ≤

≤

+ −

≤ ≤

+ ≤

≤

+

i v v f n i For

n vv andf i

v v f n

i For

n v f and i v f n i For

n i

i i i

1 = )

( +

∴

χ

avt Fn n , n>3.

Proposition 1.2.

χ

_avt(K_1,_n_,_n))=n+1, for

n

>

2

.

Proof: The double star K_1,_n_,_n is obtained from the star K_1,_n by adding a new pendent edge of the existing

n

pendent vertices. Here

v

is the apex vertex. The vertex set and edge set of K1,n,n as follows,

(

)

  

  

   

 

′ ∪

  

  

   

 

′ ∪

∪ i i i

n

i n n i

i n

n v v v and E K vv vv

K

V

∪

1 = ,

1, 1

= ,

1, ]= [ ]=

[

Then |V(K_1,_n_,_n)|=2n+1 and |E(K_1,_n_,_n)|=2n. We define }

, {1,2, )

( ) (

:V K_1, _, E K_1, _, k

f _n_n ∪ _n_n → ⋯ given by 2 = ) ( 1 = ) (

1, = ) ( 1, = )

(v n f vvn f vn 1vn1 andf vnvn

f + ₋ ′₋ ′ .

For 1≤i≤n, f(vi)=iandf(vi′)=n+1, For

1 ≤

i

≤

n

−

1

, f(vv_i)=i+1

For

1 ≤

i

≤

n

−

2

, f(v_iv_i′)=i+2. 1 = ))

( _1, _, +

∴

χ

_avt K _n_n n , for

n

>

2

.

(3)

175

Proof: The friendship graph Fn can be constructed by joining

n

copies of the cycle graph C3 with a common vertex say

v

. Thus, the vertex set and edge set are

{

v,v1,v2,⋯,v2n

}

and

{

(

) (

i i

)

}

n i i n i n v v vv F

E ₌₁ 2 1 2

2 1 = = ]

[

∪

₋ . Here |V(Fn)|=2n+1 and n

F E( n)|=3

| . Now we define f :V(Fn)∪E(Fn)→{1,2,⋯,k} given by for

n

≥

2

, For

1 ≤

i

≤

n

,

1. 2 = ) ( = ) ( 2 = ) ( 1, 2 = ) ( 3, = ) ( 2, = )

(v2−1 f v2 f vv2−1 i− f vv2 iand f v f v2−1v2 n+

f i i i i i i

1 2 = )

( +

∴

χ

_avt Fn n ,

n

≥

2

.

Proposition 1.4. The complete graph Kn admits AVDTC and

   ≡ + ≡ + 2) ( 1 2, 2) ( 0 1, = ) ( mod n if n mod n if n K_n avt

χ

Proof: Let x1,x2,⋯xn be the vertices of complete graph Kn. We define

} , {1,2, ) ( ) (

:V K E K k

f _n ∪ _n → ⋯ given by

Case-1 When n≡0 mod( 2) For 1≤i, j≤n

1 = , = ) ( = ) ( + +

+ j if i j n

i x x f i x f j i i

For i+ j≠n+1

      ≡ + +       +     + ≡ + + ≡ 2) ( 1 1), ( ) ( 2 1 2) ( 0 , 2 ) ( mod j i if n mod j i n mod j i if j i x x f _i _j

Case-2 When n≡1 mod( 2) For 1≤i, j≤n

2 = , = ) ( , = ) ( + +

+ j if i j n

i x x f i x f j i i

For i+ j≠n+2

      ≡ + +       +     + ≡ + + ≡ 2) ( 1 2), ( ) ( 2 2 2) ( 0 , 2 ) ( mod j i if n mod j i n mod j i if j i x x f i j

(4)

176

We observe that these graphs are admits the adjacent vertex distinguishing total coloring conjecture. Next, we discuss the line graph of these graphs admits AVDTC conjecture.

2. AVDTC of line graph

A graph

G

and its line graph L(G) is a graph such that each vertex of L(G) represents an edge of

G

and two vertices of L(G) are adjacent iff their corresponding edges are adjacent in

G

. In this section, the adjacent vertex distinguishing total coloring of line graph of Fan graph L(Fn), double star L(K1,n,n) and Friendship graph ( )

n

F L are discussed.

Theorem 2.1. The line graph of Fan graph L(Fn) admits

AVDTC

and

3 > 3,

= )

(F n forn

L n

avt +

χ

Proof: From the proposition (1.1), Let us consider the edges of F_n as n

i for x

vv_i = _i, 1≤ ≤ and v_iv_i₊₁= y_i, for1≤i≤n−1.

  

  

     

∪

    

 −

i n

i i n

i

n x y

F L

V

∪

1

1 = 1

= = )] ( [

Hence |V(L(Fn))|=2n−1 and

2 8 5 |= )) ( ( |

2+ − n n F L

E n . Note that {x1,x2,⋯,xn}

forms the complete graph Kn with

n

vertices. Now we define

} , {1,2, ))

( ( )) ( (

:V L F E L F k

f _n ∪ _n → ⋯ as follows. For this, first we color a clique in )

(F_n

L using the proposition (1.4). Now the remaining vertices and edges of L(F_n) are colored as follows.

Figure 1: L(F6)

Case-1. When

n

is even.

(5)

177 For 1≤i≤n−2, f(yiyi+1)=i+1.

Case-2. When

n

is odd.

For

1 ≤

i

≤

n

−

1

, f(xixi+1)= f(yi); f(xi+1yi)=n+3;

For 1≤i≤n−2, f(y_iy_i₊₁)=i+1,

For ≤ ≤  2

1 i n , f(x2iy2i)=i; i n y

x

f _i₋ _i₋  + 2 = )

( ₂ ₁ ₂ ₁ .

Hence Line graph of fan graph admits AVDTC. 3.

= )) (

( +

∴

χ

_avt L F_n n Hence the theorem.

Theorem 2.2. The line graph of double star graph L(K_1,_n_,_n) admits

AVDTC

and 3.

> 2,

= )

(K_1, _, n forn

L _n_n

avt +

χ

Proof: From the proposition (1.2), Let us consider the edges of K_1,_n_,_n as vv =_i x_i and

i i iv y

v ′= for

1 ≤

i

≤

n

. [ ( )]=

{

( )

}

1

= ,

1, i i

n

i n

n x y

K L

V

∪

∪ Hence |V(L(K_1,_n_,_n))|=2n and

2 |= )) ( ( |

2 ,

1,

n n K

L

E nn

+

. Note that {x1,x2,⋯,xn} forms the complete graph Kn with

n

vertices. Now we define f :V(L(K_1,_n_,_n))∪E(L(K_1,_n_,_n))→{1,2,⋯,k} as follows. For this, first we color a clique in L(K_1,_n_,_n) using the proposition (1.4). Now the remaining vertices and edges are colored as follows.

Figure 2: L(K_1,6,6)

Case-1. When

n

is even.

(6)

178 Case-2. When

n

is odd.

For

1 ≤

i

≤

n

, f(y_i)=n+2. For ≤ ≤  2

1 i n , f(x₂_iy₂_i)=i.

For ≤ ≤  2

1 i n , f x _i₋ y _i₋ n+i

2 = )

( ₂ ₁ ₂ ₁ .

Hence the Line graph of double star admits AVDTC. 2.

= )) (

( _1, _, +

∴

χ

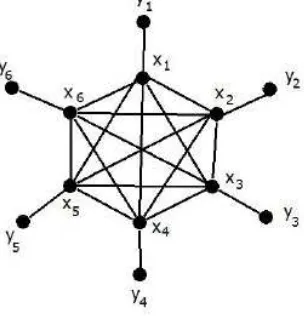
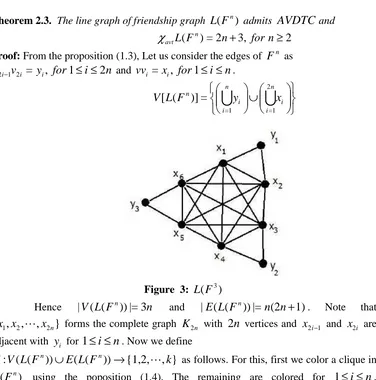
_avt L K _n_n n Hence the theorem.

Theorem 2.3. The line graph of friendship graph ( n) F

L admits

AVDTC

and

2 3,

2 = )

(F n+ forn≥

L n

avt

χ

Proof: From the proposition (1.3), Let us consider the edges of Fn as n

i for y v

v2i−1 2i = i, 1≤ ≤2 and vvi =xi, for1≤i≤n.

  

  

     

∪

     

i n

i i n

i n

x y

F L

V

∪

2

1 = 1

= = )] ( [

Figure 3: L(F3)

Hence |V(L(Fn))|=3n and |E(L(Fn))|=n(2n+1). Note that }

, , ,

{x₁ x₂ ⋯ x₂_n forms the complete graph K₂_n with

2 n

vertices and x₂_i₋₁ and x₂_i are adjacent with y_i for

1 ≤

i

≤

n

. Now we define

} , {1,2, ))

( ( )) ( (

:V L F E L F k

f n ∪ n → ⋯ as follows. For this, first we color a clique in )

( n

F

L using the poposition (1.4). The remaining are colored for 1≤i≤n, 2

= ) (x₂₋₁y n+

f _i _i ; f(x₂_ix_i)=n+3; f(y_i)= f(x₂_i₋₁x₂_i). Hence the Line graph of friendship graph admits AVDTC. ∴

χ

_avt(L(Fn))=2n+3.

3. AVDTC of splitting graph

(7)

179

corresponding to each vertex

v

of G such that N(v)= N(v′). The resultant graph is denoted as Sp(G). In this section, the adjacent vertex distinguishing total coloring of Splitting graph of path P_n, cycle C_n and star K_1,_n and sun let S2n

graphs are discussed.

Theorem 3.1. The splitting graph of path graph Sp(P_n) admits

AVDTC

and

 

 ≥

3 = 5,

4 6,

= ) (

n for

n for P

Sp n avt

χ

Proof: Let we denote {v₁,v₂,⋯,v_n} as the vertices of P_n and {v₁′,v₂′,⋯,v_n′} as the new vertices. The vertex set and edge set of Sp(P_n) are

(

)

  

  

   

 

′ ∪ ′ ∪

  

  

   

 

′

∪ + + +

−

1 1

1 = 1

=

= )] ( [ =

)] (

[ i i i i i i

n

i n

i i n

i

n v v and E Sp P vv vv vv

P Sp

V

∪

Figure 4: Sp(P5)

Hence |V(Sp(Pn))|=2n and |E(Sp(Pn))|=3(n−1). This theorem is trivial for

n

=

3

.

Now we define f :V(Sp(P_n))∪E(Sp(P_n))→{1,2,⋯,k} given by for

n

≥

4

,

6 = ) ( 5

= ) (

2) (

0 {4},

2) (

1 {3},

= ) ( 1, 1

2) (

0 {2},

2) (

1 {1},

= ) ( = ) ( , 1

1 1

1

+ +

+

′

′ 

 

≡ ≡ −

≤ ≤

  

≡ ≡ ′

≤ ≤

i i i

i

i i

v v f and v

v f

mod i

if

mod i

if v

v f n i For

mod i

if

mod i

if v

f v f n i For

Clearly, the color classes of any two adjacent vertices are different. 4.

6, = )) (

( ≥

∴

χ

avt Sp Pn n Hence the theorem.

Theorem 3.2. The splitting graph of cycle graph Sp(C_n) admits AVDTC and

4. 6, = )

(C n≥

Sp _n

avt

χ

Proof: Let we denote {v1,v2,⋯,vn} as the vertices of Cn and {v1′,v2′,⋯,vn′} as the new

(8)

180

(

)

      ′ ∪ ′ ∪ ∪       ′ ∪ ′ ∪             ′ ∪ + + + − ) ( = )] ( [ = )] ( [ 1 1 1 1 1 1 1 1 = 1 = v v v v v v v v v v v v C Sp E and v v C Sp V n n n i i i i i i n i n i i n i n

∪

Figure 5: Sp(C6)

Then |V(Sp(C_n))|=2n and |E(Sp(C_n))|=3n.

Define f :V(Sp(C_n))∪E(Sp(C_n))→{1,2,⋯,k} as follows. Case-1. When

n

is even.

   ≡ ≡ ′ ≤ ≤ 2) ( 0 2, 2) ( 1 1, = ) ( = ) ( , 1 mod i if mod i if v f v f n i

For _i _i

4. = ) ( 5, = ) ( = ) ( 6, = ) ( = ) ( 2) ( 0 4, 2) ( 1 3, = ) ( 1, 1 1 1 1 1 1 1 v v andf v v f v v f v v f v v f mod i if mod i if v v f n i For n n i i n i i i i ′ ′ ′ ′    ≡ ≡ − ≤ ≤ + + +

Case-2. When

n

is odd.

   ≡ ≡ − ≤ ≤    ≡ ≡ ′ − ≤ ≤ + 2) ( 0 4, 2) ( 1 3, = ) ( 2, 1 2) ( 0 2, 2) ( 1 1, = ) ( = ) ( 1, 1 1 mod i if mod i if v v f n i For mod i if mod i if v f v f n i For i i i i 1 = ) ( 2 = ) ( 4, = ) ( 5, = ) ( = ) ( 6, = ) ( = ) ( 1, 1 1 1 1 1 1 1 n n n n n i i n i i v v f and v v f v f v v f v v f v v f v v f n i For − + + ′ ′ ′ ′ − ≤ ≤

(9)

181 6

= )) (

( n

avt Sp C

χ

∴ .

Hence the theorem.

Theorem 3.3. The splitting graph of star graph Sp(K_1,n) admits

AVDTC

and 2.

1, 2 = )

(K_1, n+ n≥

Sp _n

avt

χ

Proof: Let {v,v₁,v₂,⋯,v_n} be the vertices of star K_1,_n and {v′,v₁′,v′₂,⋯,v′_n} be the new vertices of K_1,_n. Here

v

is the apex vertex. The vertex set and edge set of Sp(K_1,n) is given by

Figure 6: Sp(K_1,4)

(

)

   

 

′ ∪ ′ ∪

  

  

′ ∪ ∪

   

 

′

∪ i i i

n

i n i

i n

i

n v v v v andE Sp K vv vv vv

K S

V

∪

1 = 1,

1 =

1, )]= [ ( )]=

( [

Then |V(Sp(K_1,_n))|=2(n+1) and |E(Sp(K_1,_n))|=3n.

We define f :V(Sp(K_1,_n))∪E(Sp(K_1,_n))→{1,2,⋯,k} given by For 1≤i≤n,

i n v v f v v f n v f v f i v f v

f( i)= ( i′)= , ( )= ( ′)= +1, ( ′i)= ( ′ i)= +1+

For

1 ≤

i

≤

n

−

1

,

1 = ) ( 1, = )

(vv_i i f vv_n

f +

Clearly, the color classes of any two adjacent vertices are different. 2.

1, 2 = )) (

( _1, + ≥

∴

χ

_avt Sp K _n n n

Hence the theorem.

Theorem 3.4. The splitting graph of sun let graph S2n admits

AVDTC

and 4.

8, = )

(S2 n≥

Sp n

avt

χ

Proof: Let {v1,v2,⋯,vn,v1′,v2′,⋯vn′} be the vertices of sun let graph

n

S2 . Here 3

= ) (vi

deg and deg(v′i)=1 for i=1,2,⋯,n. Now consider the new vertices }

, , , , , , ,

(10)

182             ′ ∪ ∪ ′

∪ i i i

i n i n u u v v S Sp V

∪

1 = 2 = )] ( [

(

)

(

) (

)

      ∪ ∪ ∪ ′ ∪ ′ ∪ ′ ∪ ∪ ∪ + + + − n n n i i i i i i n i i i i i i i n i n u v u v v v v u u v v v u v u v v v S Sp

E ₁ ₁ ₁

1 = 1 1 1 1 1 = 2 = )] ( [

∪

Then |V(Sp(S2n))|=4n and |E(Sp(S2n))|=6n.

Figure 7: Sp(S6) We define : ( ( 2 )) ( ( 2 )) {1,2, , }

k S Sp E S Sp V

f n ∪ n → _⋯

given by Case-1.If n≡1 mod( 2).

For

1 ≤

i

≤

n

−

1

   ≡ ≡ 2) ( 0 2, 2) ( 1 1, = ) ( = ) ( mod i if mod i if u f v

f _i _i

For 1≤i≤n−2

   ≡ ≡ + 2) ( 0 4, 2) ( 1 3, = ) ( 1 mod i if mod i if v v f i i

and f(v_n)=4, f(v_nv₁)=2, f(v_n₋_{1 n}v )=1 For

1 ≤

i

≤

n

−

1

6 = ) ( = ) ( 5, = ) ( = )

(v_iu_i ₁ f v_nu₁ f v_i ₁u_i f v₁u_n

f ₊ ₊

For

1 ≤

i

≤

n

8 = ) ( = ) ( 7 = ) ( 3, = ) ( = )

(vi f ui f vivi and f uivi f viui

f ′ ′ ′ ′ ′

Case-2.If n≡0 mod( 2). For 1≤i≤n

   ≡ ≡ 2) ( 0 2, 2) ( 1 1, = ) ( = ) ( mod i if mod i if u f v

f i i

1 1≤i≤n− For 4. = ) ( 2) ( 0 4, 2) ( 1 3, = )

( ₁ and f v v₁

mod i if mod i if v v

f _i _i _n

(11)

183

6 = ) ( = ) ( 5, = ) ( = ) ( 1,

1 i n f viui 1 f vnu1 f vi1ui f v1un

For ≤ ≤ − ₊ ₊

8 = ) ( = ) ( 7

= ) ( 3, = ) ( = ) ( ,

1 i n f vi f ui f vivi and f uivi f viui

For ≤ ≤ ′ ′ ′ ′ ′

4. 8, = )) (

( 2 ≥

∴

χ

_avt Sp S n n

Therefore the splitting graph of sun let graph admits AVDTC conjecture. Hence the theorem.

4. Conclusion

We found the adjacent vertex distinguishing total chromatic number of line graph of Fan graph, double star, Friendship graph and splitting graph of path, cycle, star and sun let graph. Also, it is proved that the adjacent vertex distinguishing total coloring conjecture is true for these graphs.

Acknowledgement. The second author gratefully acknowledge The Department of Science and Technology, DST PURSE – Phase II for the financial support under the grant 686 (2014).

REFERENCES

1. N.L.Biggs, Algebraic Graph Theory, Cambridge University Press, 2nd edition, Cambridge, 1993.

2. F.Harary, Graph Theory, Narosa publishing House. (2001).

3. N.Khan, M.Pal and A.Pal, (2,1)-total labelling of cactus graphs, Journal of Information and Computing Science, 5(4) (2010) 243-260.

4. N.Khan and M.Pal, Adjacent vertex distinguishing edge colouring of cactus graphs, International Journal of Engineering and Innovative Technology, 4(3) (2013) 62-71. 5. K.K.Parthasarathy, Basic Graph Theory, Tata McGraw Hill, (1994).

6. K.Thirusangu and R.Ezhilarasi, Adjacent-vertex- distinguishing total coloring of tensor product of graphs, communicated.

7. K.Thirusangu and R.Ezhilarasi, Adjacent vertex distinguishing total coloring of quadrilateral snake, Journal of Advances in Mathematics,13 (1) (2017) 7030-7041. 8. Z.Zhang, X.Chen, L.Jingwen, B.Yao, X.Lu and J.Wang, On adjacent-vertex-