A Comparative Study of data structures for Proximity Search using Text Based Keywords
Full text
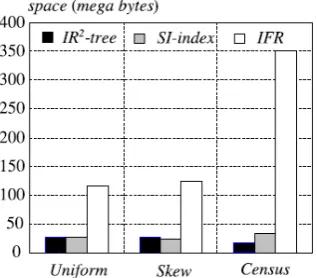
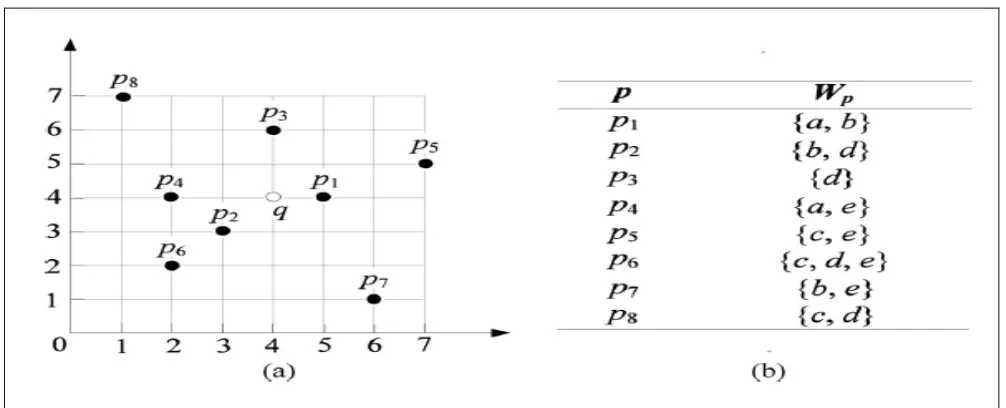
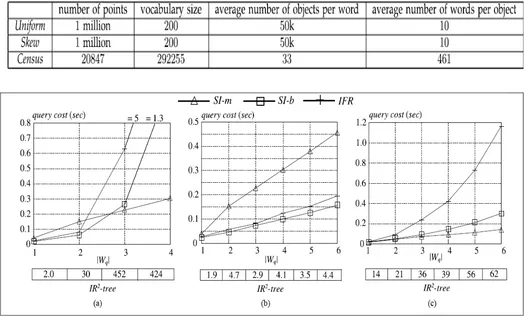
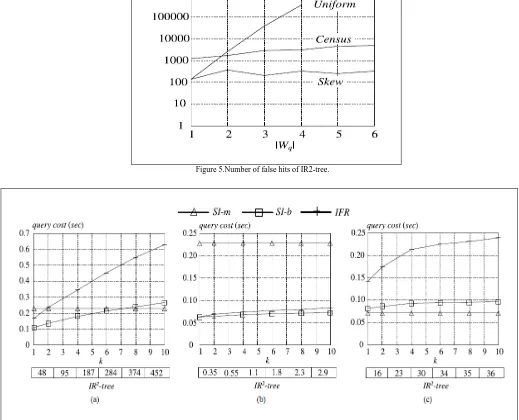
Figure

Related documents
Assessing the benefi t-risk ratio of anticoagulation is one of the most challenging issues in the individual elderly patient, patients at highest hemorrhagic risk often being those
the majority of children will respond to the intracutaneous injection of influenzal vaccine by increasing the amount of serum antibodies at least four times over the
ABSTRACT : Aiming at the poor dynamic performance and low navigation precision of traditional fading Kalman filter in BDS dynamic positioning, an improved fading
Also, both diabetic groups there were a positive immunoreactivity of the photoreceptor inner segment, and this was also seen among control ani- mals treated with a
Panoramic Viewfinder offers three main user interface elements designed to help complete the desired panorama, i.e., (1) the preview shows the panorama in its current state
The use of sodium polyacrylate in concrete as a super absorbent polymer has promising potential to increase numerous concrete properties, including concrete
The paper assessed the challenges facing the successful operations of Public Procurement Act 2007 and the result showed that the size and complexity of public procurement,
Nevertheless, all the analyzed papers showed that the photoprotective effect of plant extracts rich in polyphenols, especially flavonoids and their additive and synergistic