R E S E A R C H
Open Access
Oscillation deduced from the Neimark-Sacker
bifurcation in a discrete dual Internet
congestion control algorithm
Yingguo Li
**Correspondence: yguoli@fjnu.edu.cn School of Mathematics and Computer Science, Fujian Normal University, Fuzhou, Fujian, 350007, P.R. China
Abstract
In this paper, we consider a dual Internet congestion control algorithm applied to a nonstandard finite-difference scheme, which responds to congestion signals from the network. By choosing delay as a bifurcation parameter, the local asymptotic stability of the positive equilibrium and the existence of Neimark-Sacker bifurcations are analyzed. Then the explicit algorithm for determining the direction of Neimark-Sacker bifurcations and the stability of invariant closed curves are derived. In addition, we give specific examples to illustrate the phenomenon that coincides with our theoretical results.
MSC: 34K18; 34K20
Keywords: dual congestion control; Neimark-Sacker bifurcation; stability; time delay; discrete dynamic system
1 Introduction
Congestion control algorithms and active queue management (AQM) for Internet have been the focus of intense research since the seminal work of Kellyet al.[]. Congestion control schemes can be divided into three classes: primal algorithms, dual algorithms and primal-dual algorithms []. In primal algorithms, the users adapt the source rates dynam-ically based on the route prices (the congestion signal generated by the link), and the links select a static law to determine the link prices directly from the arrival rates at the links. However, in dual algorithms, the links adapt the link prices dynamically based on the link rates, and the users select a static law to determine the source rates directly from the route prices and the source parameters. Primal-dual algorithms combine these two schemes and dynamically compute both user rates and link prices. In [], a stability condition was pro-vided for a single proportionally fair congestion controller with delayed feedback. Since then, this result was extended to networks in [, ]. In [], the author studied the case of a network with users having arbitrary propagation delays to and from any links in the net-work. In [], the authors studied a more general network with different roundtrip delays amongst different TCP connections.
In this paper, we consider a dual congestion control algorithm, which can be formulated as a congestion control system with feedback delay. The model is described by [, ]
˙
p(t) =kp(t)fp(t–τ)–c, (.)
wheref(·) is a non-negative continuous, strictly decreasing demand function and has at
least third-order continuous derivatives. The scalarcis the capacity of the bottleneck link and the variablepis the price at the link.kis a positive gain parameter,τ is the sum of forward and return delays. A great deal of research has been devoted to the global stability, periodic solutions and other properties of this model, for which we refer to [, ].
Considering the need of scientific computation and real-time simulation, our interest is focused on the behaviors of a discrete dynamics system corresponding to (.). In this paper, we use a nonstandard finite-difference scheme [, ] to make the discretization for system (.). Firstly, we consider the autonomous delay differential equations
˙
u(t) =fu(t),u(t– ). Then we get the following:
un+–un=(h)f(un,un–m), (.)
with the functionsuch that
(h) =h+Oh,
whereh=m (m∈Z+) stands for stepsize, andukdenotes the approximate value tou(kh).
This method can be seen as a modified forward Euler method.
The Neimark-Sacker bifurcation is the discrete analogue of the Hopf bifurcation that occurs in continuous systems. The Hopf bifurcation is extremely important in the contin-uous dual congestion control algorithm [, ]. Similarly, the Neimark-Sacker bifurcation is also highly relevant to the discrete dual congestion control algorithm. The purpose of this paper is to discuss this version as a discrete dynamical system by using Neimark-Sacker bifurcation theory of discrete systems.
The paper is organized as follows. In Section , we analyze the distribution of the char-acteristic equation associated with the discrete model and obtain the existence of the local Neimark-Sacker bifurcation. In Section , the direction and stability of a closed invariant curve from the Neimark-Sacker bifurcation of the discrete delay model are determined by using the theories of discrete systems in []. In Section , some computer simulations are performed to illustrate the theoretical results. Conclusions are given in the final section.
2 Neimark-Sacker bifurcation analysis
Letu(t) =p(τt). Then (.) can be rewritten as
˙
u(t) =τku(t)fu(t– )–c. (.)
Assume Eq. (.) has a positive equilibrium pointu*. Thenu*satisfies
fu*=c.
If we employ the nonstandard finite-difference scheme (.) to Eq. (.) and choose the functionas
(h) = –e –τkh
it yields the delay difference equation
Note that u* also is the unique positive equilibrium of (.). Sety
n=un–u*, then it
Clearly the origin is an equilibrium of (.), and the linear part of (.) is
Yn+=AYn,
The characteristic equation ofAis given by
a(λ) :=λm+–λm– –e–τkhu*fu*= . (.)
It is well known that the stability of the zero equilibrium solution of (.) depends on the distribution of zeros of the roots of (.). In this paper, we employ the results from Zhang
et al.[] and Heet al.[] to analyze the distribution of zeros of characteristic Eq. (.). In order to prove the existence of the local Neimark-Sacker bifurcation at equilibrium, we need some lemmas as follows.
Lemma . There exists aτ¯> such that for <τ<τ¯all roots of(.)have modulus less
than one.
Proof Whenτ= , (.) becomes
λm+–λm= .
Consider the rootλ(τ) such thatλ() = . This root depends continuously onτ and is a differential function ofτ. From (.), we have
dλ
Noticingf(·) is a non-negative continuous, strictly decreasing function, we have
d|λ| in the unit circle for sufficiently small positiveτ> , and the existence of theτ¯follows.
A Neimark-Sacker bifurcation occurs when a complex conjugate pair of eigenvalues of
Across the unit circle asτ varies. We have to find values ofτ such that there are roots on the unit circle. Denote the roots on the unit circle byeiω*,ω*∈(–π,π). Since we are dealing with complex roots of a real polynomial, we only need to look forω*∈(,π).
Lemma . There exists an increasing sequence of values of the time delay parameterτ=
τj,j= , , , . . . , [m–]satisfying
Separating the real part and the imaginary part from Eq. (.), there are
Then the rootseiω*of (.) satisfy Eqs. (.)-(.). From (.) we get
Substituting (.) into (.), we have
sin(m+ )ω*=sinmω*. (.)
This completes the proof.
Lemma . Letλj(τ) =rj(τ)eiωj(τ) be a root of(.)nearτ =τj satisfying rj(τj) = and
Proof From (.) and (.), we obtain that
cosmωj=
Lemmas .-. immediately lead to the stability of the zero equilibrium of Eq. (.), and equivalently, of the positive equilibriumu*of Eq. (.). So, we have the following results on stability and bifurcation in system (.).
Theorem . There exists a sequence of values of the time-delay parameter <τ<τ<
· · ·<τ[m–
] such that the positive equilibrium u
* of Eq. (.)is asymptotically stable for
τ ∈[,τ)and unstable forτ>τ.Equation(.)undergoes a Neimark-Sacker bifurcation
at the positive equilibrium u*whenτ=τ
j,j= , , , . . . , [m–],whereτjsatisfies(.).
3 Direction and stability of the Neimark-Sacker bifurcation
In the previous section, we have obtained the conditions under which a family of invariant closed curves bifurcates from the steady state at the critical valueτ =τj,j= , , , . . . , [m–]. Without loss of generality, denote the critical valueτ =τjbyτ*. In this section, following
the idea of Hassardet al.[], we study the direction and stability of the invariant closed curve whenτ=τin the discrete Internet congestion control model. The method we use is based on the theories of a discrete system by Kuznetsov [].
Rewrite Eq. (.) as
So, system (.) is turned into
We also introduce an adjoint eigenvectorq*=q*(τ)∈Cm+having the properties
ATq*=e–iωq*, ATq¯*=eiωq¯*,
and satisfying the normalizationq*,q= , whereq*,q=mi=q¯*iqi.
Lemma .(See []) Define a vector-valued function q:C→Cm+by
p(ξ) =ξm,ξm–, . . . , T. (.)
Ifξis an eigenvalue of A,then Ap(ξ) =ξp(ξ).
In view of Lemma ., we have
q=peiω=eimω,ei(m–)ω, . . . ,eiω, T. (.)
Lemma . Suppose q*= (q*
,q*, . . . ,q*m)T is the eigenvector of AT corresponding to the eigenvalue e–iω,andq*,q= .Then
q*=D¯,αeimω,αei(m–)ω, . . . ,αeiω,αeiωT, (.)
whereα= ( –e–τkh)u*f(u*)and
D=eimω+mαe–iω–. (.)
Proof Assignq*satisfiesATq*=zq¯ *withz¯=e–iω, then the following identities hold:
q*
k=e–i
ωq*
k–, k= , . . . ,m,
αq*=e–iωq*m.
(.)
Letq*m=αeiωD¯, then
q*=D¯,αeimω,αei(m–)ω, . . . ,αeiω,αeiωT.
From normalizationq*,q= and computation, Eq. (.) holds.
Leta(λ) be a characteristic polynomial ofAandλ=eiω. Following the algorithms in [] and using a computation process similar to that in [], we can compute an expression for the critical coefficientc(τ),
c(τ) =
gg( – λ) (λ–λ)
+ |g|
–λ¯
+ |g|
(λ –λ¯)
+g
, (.)
where
g=
q*,B(q,q), g=
q*,B(q,q¯), g=
q*,B(¯q,q¯),
g=
q*,B(¯q,ω)
+ q*,B(q,ω)
and
Then an invariant closed curve, topologically equivalent to a circle, for map (.) ex-ists forτ in a one side neighborhood ofτ*. The radius of the invariant curve grows like
O(|τ–τ*|). One of the four cases below applies.
Theorem . For Eq. (.),the positive equilibrium u* is asymptotically stable forτ ∈
[,τ)and unstable forτ >τ.An attracting(repelling)invariant closed curve exists for
τ >τifRe[e–iωc(τ)] < (> ).
4 Computer simulation
In this section, we confirm our theoretical analysis by numerical simulation. We choose
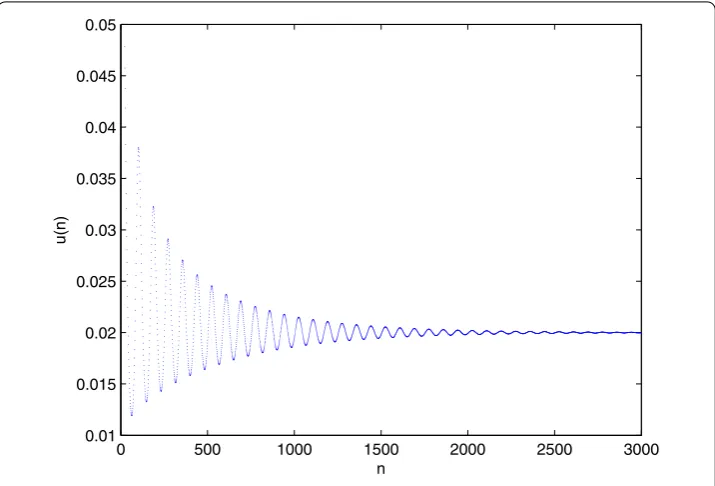
Figure 1 The equilibriumu*of (2.2) is asymptotically stable forτ= 2.9 <τ 0= 3.0.
Figure 2 Phase plot of (2.2) on the plane (u(n),u(n– 20)) forτ= 2.9 <τ0= 3.0.
Figures - are about delay difference Eq. (.) when step sizeh= ..
In Figures and , we show the waveform plot and phase plot for (.) with initial values
uj= . (j= , , . . . , ) forτ = . <τ= .. The equilibriumu*= . of Eq. (.) is asymptotically stable. In Figures and we show the waveform plot and phase plot for (.) with initial valuesuj= . (j= , , . . . , ). The equilibriumu*= . of (.) is
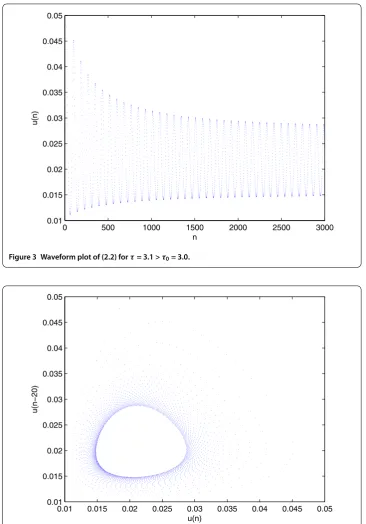
Figure 3 Waveform plot of (2.2) forτ= 3.1 >τ0= 3.0.
Figure 4 A bifurcating periodic solution appears on the plane (u(n),u(n– 20)) forτ= 3.1 >τ0= 3.0.
loses its stability and an invariant closed curve bifurcates from the equilibrium forτ= . >
τ= .. That is the delay difference Eq. (.) which has a Neimark-Sacker bifurcation atτ.
5 Conclusion
bifur-cation parameter, we have shown that when the communibifur-cation delay of the system passes through a critical value, a family of periodic orbits bifurcates from the equilibrium point. Furthermore, we have analyzed the stability and direction of the bifurcating periodic so-lutions. The results of numerical simulations agree with the theoretical results very well and verify the theoretical analysis.
Competing interests
The author declares that he has no competing interests.
Acknowledgements
The author is grateful to anonymous referees for their excellent suggestions, which greatly improved the paper. Also, this work was supported by the Foundation of Fujian Education Bureau (JB12046).
Received: 14 February 2013 Accepted: 24 April 2013 Published: 13 May 2013 References
1. Kelly, FP, Maulloo, A, Tan, DK: Rate control in communication networks: shadow prices, proportional fairness, and stability. J. Oper. Res. Soc.49, 237-252 (1998)
2. Liu, S, Basar, T, Srikant, R: Exponential-RED: a stabilizing AQM scheme for low-and high-speed TCP protocols. IEEE/ACM Trans. Netw.13(5), 1068-1081 (2005)
3. Kelly, FP: Models for a self-managed Internet. Philos. Trans. R. Soc. Lond. A358, 2335-2348 (2000)
4. Massoulie, L: Stability of distributed congestion control with heterogeneous feedback delays. IEEE Trans. Autom. Control47, 895-902 (2002)
5. Wang, XF, Chen, G, Ko, KT: A stability theorem for Internet congestion control. Syst. Control Lett.45, 81-85 (2002) 6. Wiggins, S: Introduction to Applied Nonlinear Dynamical System and Chaos. Springer, New York (1990) 7. Raina, G: Local bifurcation analysis of some dual congestion control algorithms. IEEE Trans. Autom. Control50(8),
1135-1146 (2005)
8. Ding, D, Zhu, J, Luo, X, Liu, Y: Delay induced Hopf bifurcation in a dual model of Internet congestion control algorithm. Nonlinear Anal., Real World Appl.10, 2873-2883 (2009)
9. Zhang, C, Zu, Y, Zheng, B: Stability and bifurcation of a discrete red blood cell survival model. Chaos Solitons Fractals
28, 386-394 (2006)
10. He, Z, Lai, X, Hou, A: Stability and Neimark-Sacker bifurcation of numerical discretization of delay differential equations. Chaos Solitons Fractals41, 2010-2017 (2009)
11. Mickens, RE: A nonstandard finite-difference scheme for the Lotka-Volterra system. Appl. Numer. Math.45, 309-314 (2003)
12. Su, H, Ding, X: Dynamics of a nonstandard finite-difference scheme for Mackey-Glass system. J. Math. Anal. Appl.344, 932-941 (2008)
13. Kuznetsov, YA: Elements of Applied Bifurcation Theory. Springer, New York (1995)
14. Hassard, BD, Kazarinoff, ND, Wa, YH: Theory and Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)
15. Wulf, V: Numerical Analysis of Delay Differential Equations Undergoing a Hopf Bifurcation. University of Liverpool, Liverpool (1999)
doi:10.1186/1687-1847-2013-136