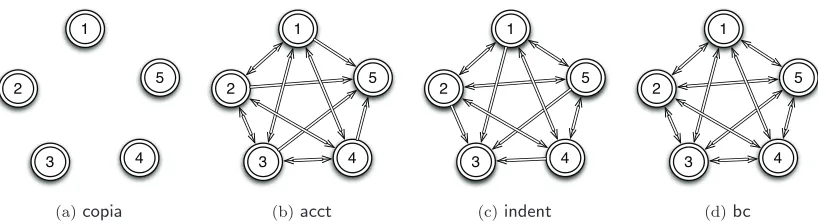
Coherent clusters in source code
Full text
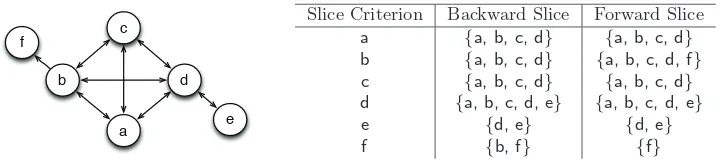
Figure
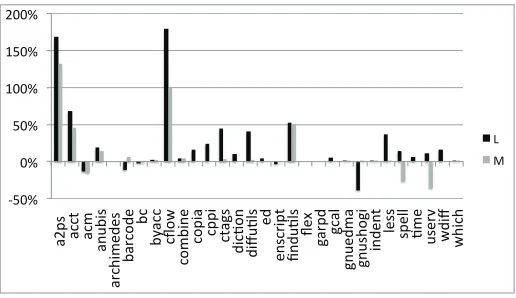
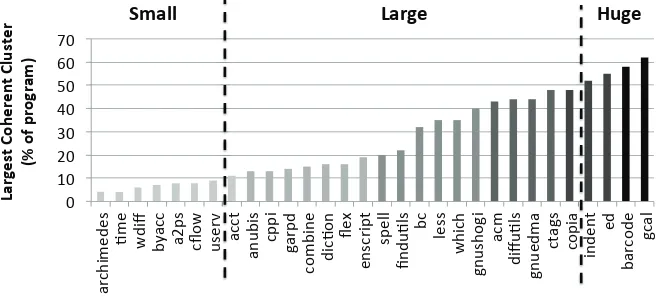
Related documents
Since cerebral amyloid angiopathy is an almost invariable pathological finding in Alzheimer’s disease, we hypothesized that MRI-visible perivascular spaces in the
Pairwise variation analysis recommended four and two reference genes for optimal normalization of the expression data of canine OS tumors and cell lines, respectively..
BGK Approximation -Single Relaxation Time (SRT) ... Multi-Relaxation Time -MRTLBM ... Regularized –Lattice Boltzmann -RLBM ... Regularized Multi-Relaxation Time -RMRTLBM ...
Thus, from the style of its architecture and decoration, Ribāṭ-i Māhī is closely related to Ribāṭ-i Šaraf, and in turn, both caravanserais show a very close similarity in
Genome-wide association study in a Chinese Han population identifies nine new susceptibility loci for systemic lupus erythematosus.. Genome-wide association study in Asian
Before Now Handwriting Signature Digital Signed PDF Party A’s Digital Signature Party B’s Digital Signature PDF417 Original Document with Digest Digital signed QR
Our water quality results are consistent with the observed data gathered at each site, projecting Rodney’s Rock as a less healthy reef system, indicated by bleaching of brain
NLM’s advanced systems disseminate many types of information essential to research and health, including genetic, genomic, and biochemical data; images; published and unpublished