Journal of Inequalities and Applications Volume 2009, Article ID 458134,20pages doi:10.1155/2009/458134
Research Article
Self-Adaptive Implicit Methods for Monotone
Variant Variational Inequalities
Zhili Ge and Deren Han
Institute of Mathematics, School of Mathematics and Computer Science, Nanjing Normal University, Nanjing 210097, China
Correspondence should be addressed to Deren Han,handr00@hotmail.com
Received 26 January 2009; Accepted 24 February 2009
Recommended by Ram U. Verma
The efficiency of the implicit method proposed by He1999depends on the parameterβheavily; while it varies for individual problem, that is, different problem has different “suitable” parameter, which is difficult to find. In this paper, we present a modified implicit method, which adjusts the parameterβautomatically per iteration, based on the message from former iterates. To improve the performance of the algorithm, an inexact version is proposed, where the subproblem is just solved approximately. Under mild conditions as those for variational inequalities, we prove the global convergence of both exact and inexact versions of the new method. We also present several preliminary numerical results, which demonstrate that the self-adaptive implicit method, especially the inexact version, is efficient and robust.
Copyrightq2009 Z. Ge and D. Han. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
LetΩbe a closed convex subset ofRnand letFbe a mapping fromRninto itself. The so-called finite-dimensional variant variational inequalities, denoted by VVIΩ, F, is to find a vector u∈ Rn, such that
Fu∈Ω, v−Fuu≥0, ∀v∈Ω, 1.1
while a classical variational inequality problem, abbreviated by VIΩ, f, is to find a vector x∈Ω, such that
x−xfx≥0, ∀x∈Ω, 1.2
Both VVIΩ, Fand VIΩ, fserve as very general mathematical models of numerous applications arising in economics, engineering, transportation, and so forth. They include some widely applicable problems as special cases, such as mathematical programming problems, system of nonlinear equations, and nonlinear complementarity problems, and so forth. Thus, they have been extensively investigated. We refer the readers to the excellent monograph of Faccinei and Pang 1, 2 and the references therein for theoretical and algorithmic developments on VIΩ, f, for example,3–10, and11–16for VVIΩ, F.
It is observed that ifF is invertible, then by settingf F−1, the inverse mapping of F,VVIΩ, F can be reduced to VIΩ, f. Thus, theoretically, all numerical methods for solving VIΩ, fcan be used to solve VVIΩ, F. However, in many practical applications, the inverse mappingF−1may not exist. On the other hand, even if it exists, it is not easy to find it. Thus, there is a need to develop numerical methods for VVIΩ, Fand recently, the Goldstein’s type method was extended from solving VIΩ, fto VVIΩ, F 12,17.
In11, He proposed an implicit method for solving general variational inequality problems. A general variational inequality problem is to find a vectoru∈ Rn, such that
Fu∈Ω, v−FuGu≥0, ∀v∈Ω. 1.3
WhenGis the identity mapping, it reduces to VVIΩ, Fand ifFis the identity mapping, it reduces to VIΩ, G. He’s implicit method is as follows.
S0Givenu0∈Rn, β >0, γ ∈0,2, and a positive definite matrixM.
S1Finduk1via
θku 0, 1.4
where
θku Fu βGu−F
uk−βGuk
γρuk, M, βM−1euk, β, 1.5
ρuk, M, β euk, β
2
euk, βM−1euk, β,
eu, β: Fu−PΩFu−βGu,
1.6
withPΩbeing the projection fromRnontoΩ, under the Euclidean norm.
He’s method is attractive since it solves the general variational inequality problem, which is essentially equivalent to a system of nonsmooth equations
eu, β 0, 1.7
to solve it. Furthermore, to improve the efficiency of the algorithm, He11proposed to solve the subproblem approximately. That is, at Step 1, instead of finding a zero ofθk, it only needs to find a vectoruk1satisfying
θk
uk1≤η
ke
uk, β, 1.8
where{ηk} is a nonnegative sequence. He proved the global convergence of the algorithm under the condition that the error tolerance sequence{ηk}satisfies
∞
k 0
ηk2<∞. 1.9
In the above algorithm, there are two parametersβ >0 andγ∈0,2, which affect the efficiency of the algorithm. It was observed that nearly for all problems,γclose to 2 is a better choice than smallerγ, while different problem has differentoptimalβ. A suitable parameterβ is thus difficult to find for an individual problem. For solving variational inequality problems, He et al.18proposed to choose a sequence of parameters{βk}, instead of a fixed parameter
β, to improve the efficiency of the algorithm. Under the same conditions as those in11, they proved the global convergence of the algorithm. The numerical results reported there indicated that for any given initial parameterβ0, the algorithm can find a suitable parameter
self-adaptively. This improves the efficiency of the algorithm greatly and makes the algorithm easy and robust to implement in practice.
In this paper, in a similar theme as18, we suggest a general rule for choosing suitable parameter in the implicit method for solving VVIΩ, F. By replacing the constant factor β in1.4and1.5with a self-adaptive variable positive sequence{βk}, the efficiency of the
algorithm can be improved greatly. Moreover, it is also robust to the initial choice of the parameterβ0. Thus, for any given problems, we can choose a parameter β0 arbitrarily, for
example, β0 1 or β0 0.1. The algorithm chooses a suitable parameter self-adaptively,
based on the information from the former iteration, which makes it able to add a little additional computational cost against the original algorithm with fixed parameter β. To further improve the efficiency of the algorithm, we also admit approximate computation in solving the subproblem per iteration. That is, per iteration, we just need to find a vectoruk1
that satisfies1.8.
Throughout this paper, we make the following assumptions.
Assumption A. The solution set of VVIΩ, F, denoted byΩ∗, is nonempty.
Assumption B. The operatorFis monotone, that is, for anyu, v∈ Rn,
u−vFu−Fv≥0. 1.10
The rest of this paper is organized as follows. InSection 2, we summarize some basic properties which are useful in the convergence analysis of our method. In Sections3 and
2. Preliminaries
For a vector x ∈ Rn and a symmetric positive definite matrix M ∈ Rn×n, we denote x √xxas the Euclidean-norm andx
Mas the matrix-induced norm, that is,xM :
xMx1/2
.
LetΩbe a nonempty closed convex subset ofRn, and letPΩ·denote the projection
mapping fromRnontoΩ, under the matrix-induced norm. That is,
PΩx: arg minx−yM, y∈Ω. 2.1
It is known12,19that the variant variational inequality problem1.1is equivalent to the projection equation
Fu PΩ
Fu−βM−1u, 2.2
whereβis an arbitrary positive constant. Then, we have the following lemma.
Lemma 2.1. u∗ is a solution of VVIΩ, Fif and only ifeu, β 0for any fixed constantβ > 0, where
eu, β: Fu−PΩ
Fu−βM−1u 2.3
is the residual function of the projection equation2.2.
Proof. See11, Theorem 1.
The following lemma summarizes some basic properties of the projection operator, which will be used in the subsequent analysis.
Lemma 2.2. LetΩ be a closed convex set inRn and letPΩ denote the projection operator onto Ω
under the matrix-induced norm, then one has
w−PΩvMv−PΩv≤0, ∀v∈ Rn,∀w∈Ω, 2.4
PΩu−PΩvM≤ u−vM, ∀u, v∈ Rn. 2.5
The following lemma plays an important role in convergence analysis of our algorithm.
Lemma 2.3. For a givenu∈ Rn, letβ≥β >0.Then it holds that
eu,β
M≥eu, βM. 2.6
Lemma 2.4. Letu∗∈Ω∗, then for allu∈ Rnandβ >0, one has
{Fu−Fu∗ βM−1u−u∗}Meu, β≥eu, β2
M. 2.7
Proof. It follows from the definition of VVIΩ, F see1.1that
{PΩFu−βM−1u−Fu∗}βu∗≥0. 2.8
By settingv: Fu−βM−1uandw: Fu∗in2.4, we obtain
{PΩFu−βM−1u−Fu∗}M
eu, β−βM−1u≥0. 2.9
Adding2.8and2.9, and using the definition ofeu, βin2.3, we get
{Fu−Fu∗−eu, β}Meu, β−βM−1u−u∗≥0, 2.10
that is,
Fu−Fu∗ βM−1u−u∗Meu, β
≥eu, β2
MβFu−Fu∗u−u∗
≥eu, β2
M,
2.11
where the last inequality follows from the monotonicity ofFAssumption B. This completes the proof.
3. Exact Implicit Method and Convergence Analysis
We are now in the position to describe our algorithm formally.
3.1. Self-Adaptive Exact Implicit Method
S0Givenγ∈0,2,β0>0,u0∈ Rnand a positive definite matrixM.
S1Computeuk1such that
Fuk1β
kM−1 uk1−F
uk−β
kM−1 ukγe
uk, β
k
S2If the given stopping criterion is satisfied, then stop; otherwise choose a new parameterβk1 ∈1/1τkβk,1τkβk, whereτksatisfies
∞
k 0
τk<∞, τk≥0. 3.2
Setk: k1 and go to Step 1.
From3.1, we know thatuk1is theexactunique zero of
θku: Fu βkM−1u−F
uk−β
kM−1ukγe
uk, β
k
. 3.3
We refer to the above method asthe self-adaptive exact implicit method.
Remark 3.1. According to the assumptionτk ≥ 0 and∞k 0τk < ∞, we have∞k 01τk <
∞. Denote
Sτ :
∞
k 0
1τk. 3.4
Hence, the sequence{βk} ⊂ 1/Sτβ0, Sτβ0is bounded. Then, let inf{βk}∞k 0 : βL > 0 and
sup{βk}∞k 0: βU<∞.
Now, we analyze the convergence of the algorithm, beginning with the following lemma.
Lemma 3.2. Let{uk}be the sequence generated by the proposed self-adaptive exact implicit method. Then for anyu∗∈Ω∗andk >0, one has
Fuk1−Fu∗ β
kM−1uk1−u∗
2
M
≤Fuk−Fu∗ β
kM−1uk−u∗
2
M−γ
2−γeuk, β k
2
M.
3.5
Proof. Using3.1, we get
Fuk1−Fu∗ β
kM−1uk1−u∗
2
M
Fuk−Fu∗ β
kM−1uk−u∗−γeuk, βk
2
M
≤Fuk−Fu∗ β
kM−1uk−u∗
2
M−2γ
euk, β
k
2
Mγ
2euk, β k
2
M
Fuk−Fu∗ β
kM−1uk−u∗
2
M−γ
2−γeuk, βk
2
M,
3.6
Since 0< βk1 ≤1τkβkandFis monotone, it follows that
Fuk1−Fu∗ β
k1M−1uk1−u∗ 2
M
Fuk1−Fu∗ β
kM−1uk1−u∗ βk1−βkM−1uk1−u∗
2
M
Fuk1−Fu∗ β
kM−1uk1−u∗
2
M βk1−βk
2uk1−u∗2
M
2βk1−βkuk1−u∗
Fuk1−Fu∗β
kM−1
uk1−u∗
≤1τk2Fuk1−Fu∗ β
kM−1uk1−u∗
2
M,
3.7
where the inequality follows from the monotonicity of the mappingF. Combining3.5and
3.7, we have
Fuk1−Fu∗ β
k1M−1uk1−u∗ 2
M
≤1τk2Fuk−Fu∗ β
kM−1uk−u∗
2
M−γ
2−γeuk, β k
2
M.
3.8
Now, we give the self-adaptive rule in choosing the parameter βk. For the sake of balance, we hope that
Fuk1−Fuk M≈
βkM−1uk1−ukM. 3.9
That is, for given constantτ >0, if
Fuk1−Fuk
M>1τ
βkM−1uk1−ukM, 3.10
we should increaseβkin the next iteration; on the other hand, we should decreaseβkwhen
Fuk1−Fuk M<
1
1τ
βkM−1uk1−uk
M. 3.11
Let
ωk
Fuk1−Fuk M
βkM−1uk1−uk M
Then we give
βk1:
⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩
1τkβk, ifωk>1τ,
1
1τkβk, ifωk< 1
1τ, βk, otherwise.
3.13
Such a self-adaptive strategy was adopted in18,21–24for solving variational inequality problems, where the numerical results indicated its efficiency and robustness to the choice of the initial parameter β0. Here we adopted it for solving variant variational inequality
problems.
We are now in the position to give the convergence result of the algorithm, the main result of this section.
Theorem 3.3. The sequence {uk} generated by the proposed self-adaptive exact implicit method converges to a solution of VVIΩ, F.
Proof. Letξk: 2τkτk2. Then from the assumption that∞
k 0τk<∞, we have that
∞
k 0ξk<
∞, which means that∞k 01ξk<∞. Denote
Cs:
∞
i 0
ξi, Cp:
∞
i 0
1ξi. 3.14
From3.8, for anyu∗∈Ω∗, that is, an arbitrary solution of VVIΩ, F, we have
Fuk1−Fu∗ β
k1M−1uk1−u∗ 2
M
≤1ξkFuk−Fu∗ βkM−1uk−u∗
2
M
≤ k
i 0
1ξi
Fu0−Fu∗ β
0M−1u0−u∗ 2
M
3.15
≤CpFu0−Fu∗ β0M−1u0−u∗ 2
M
<∞.
3.16
Also from3.8, we have
γ2−γeuk, βk
2
M≤1τk
2Fuk−Fu∗ β
kM−1uk−u∗
2
M
−Fuk1−Fu∗ β
k1M−1uk1−u∗ 2
M
Fuk−Fu∗ β
kM−1uk−u∗
2
M
−Fuk1−Fu∗ β
k1M−1uk1−u∗ 2
M
ξkFuk−Fu∗ βkM−1uk−u∗
2
M.
3.17
Adding both sides of the above inequality, we obtain
γ2−γ ∞
k k0
euk, β
k
2
M
≤Fu0−Fu∗ β
0M−1u0−u∗ 2
M
∞
k 0
ξkFuk−Fu∗ βkM−1uk−u∗
2
M
≤Fu0−Fu∗ β
0M−1u0−u∗ 2
M
∞
k 0
ξk
CpFu0−Fu∗ β0M−1u0−u∗ 2
M
1CsCpFu0−Fu∗ β0M−1u0−u∗ 2
M
<∞,
3.18
where the second inequality follows from3.15. Thus, we have
lim
k→ ∞
euk, β
k
M 0, 3.19
which, fromLemma 2.3, means that
lim
k→ ∞
euk, β
LM≤ lim k→ ∞
euk, β
Since{uk}is bounded, it has at least one cluster point. Letube a cluster point of{uk} and let{ukj}be the subsequence converging tou. Sinceeu, βLis continuous, taking limit in
3.20along the subsequence, we get
eu, βL
M jlim→ ∞eukj, βLM 0. 3.21
Thus, fromLemma 2.1,uis a solution of VVIΩ, F.
In the following we prove that the sequence{uk}has exactly one cluster point. Assume thatuis another cluster point of{uk}, which is different fromu. Becauseuis a cluster point of the sequence{uk}andFis monotone, there is ak0>0 such that
Fuk0−Fu β
k0M−
1uk0−u
M≤
δ
2Cp, 3.22
where
δ: Fu−Fu βk0M
−1u−u
M. 3.23
On the other hand, sinceu∈Ω∗ andu∗is an arbitrary solution, by settingu∗ : uin3.15, we have for allk≥k0,
Fuk−Fu β
kM−1uk−u
2
M
≤k
i k0
1ξiFui−Fu β
iM−1ui−u
2
M
≤CpFuk0−Fu β
k0M−
1uk0−u2
M,
3.24
that is,
Fuk−Fu β
kM−1uk−uM
≤C1/2
p Fuk0−Fu βk0M−
1uk0−u
M
≤ δ 2C1/2
p
.
Then,
Fuk−Fu β
kM−1uk−uM
≥Fu−Fu βkM−1u−uM
−Fuk−Fu β
kM−1uk−u M.
3.26
Using the monotonicity ofFand the choosing rule ofβk, we have
Fu−Fu βkM−1u−u
2
M
Fu−Fu βk−1M−1u−u βk−βk−1M−1u−u 2
M
Fu−Fu βk−1M−1u−u 2
M
βk−βk−1M−1u−u 2
M
2βk−βk−1
u−uTFu−Fu βk−1M−1u−u
≥ 1
1τk−12
Fu−Fu βk−1M−1u−u 2
M
≥ C1
p
Fu−Fu βk0M−
1u−u2
M.
3.27
Combing3.25–3.27, we have that for anyk≥k0,
Fuk−Fu β
kM−1uk−uM
≥ δ C1/2
p
− δ 2C1/2
p
δ 2C1/2
p
>0,
3.28
which means thatucannot be a cluster point of{uk}. Thus,{uk}has just one cluster point.
4. Inexact Implicit Method and Convergence Analysis
is, for a givenuk, instead of finding the exact solution of3.1, we would acceptuk1 as the
new iterate if it satisfies
Fuk1−Fuk β
kM−1uk1−uk γeuk, βkM≤ηkeuk, βkM, 4.1
where{ηk}is a nonnegative sequence with∞k 0ηk2 < ∞. If3.1is replaced by4.1, the
modified method is calledinexact implicit method.
We now analyze the convergence of the inexact implicit method.
Lemma 4.1. Let{uk}be the sequence generated by the inexact implicit method. Then there exists a k0>0such that for anyk≥k0andu∗∈Ω∗,
Fuk1−Fu∗ β
kM−1uk1−u∗
2
M
≤
1 4ηk
2
γ2−γ
Fuk−Fu∗ β
kM−1uk−u∗
2
M
−1 2γ
2−γeuk, βk
2
M.
4.2
Proof. Denote
θku: Fu−F
ukβ
kM−1
u−ukγeuk, β k
. 4.3
Then4.1can be rewritten as
θkuk1M≤ηkeuk, βkM. 4.4
According to4.3and2.7,
Fuk1−Fu∗ β
kuk1−u∗
2
M
Fuk−Fu∗ β
kM−1uk−u∗−γeuk, βk−θkuk1
2
M
≤Fuk−Fu∗ β
kM−1uk−u∗
2
M−2γ
euk, β
k
2
M
2{Fuk−Fu∗ β
kM−1uk−u∗}Mθk
uk1
γeuk, β
k−θkuk1
2
M.
Using Cauchy-Schwarz inequality and4.4, we have
2{Fuk−Fu∗ β
kM−1uk−u∗}Mθk
uk1
≤ 4ηk2 γ2−γ
Fuk−Fu∗ β
kM−1uk−u∗
2
M
γ2−γ 4ηk2
θkuk1
2
M
≤ 4ηk2 γ2−γ
Fuk−Fu∗ β
kM−1uk−u∗
2
M
γ2−γ 4
euk, β
k
2
M,
4.6
γeuk, β
k−θkuk1
2
M
γ2euk, β
k
2
M−2γe
uk, β
k
T Mθk
uk1θ
kuk1
2
M
≤γ2euk, β
k
2
M
γ2−γ 8
euk, β
k
2
M
8γ
2−γ
θkuk1
2
M
θkuk1
2
M
≤γ2euk, β k
2
M
γ2−γ 8
euk, β
k
2
M
1 8γ 2−γ
η2
keuk, βk
2
M.
4.7
Since∞k 0η2
k<∞, there is a constantk0≥0, such that for allk≥k0,
1 8γ 2−γ
η2
k≤
γ2−γ
8 , 4.8
and4.7becomes that for allk≥k0,
γeuk, β
k−θkuk1
2
M≤γ
2euk, β k
2
M
γ2−γ 4
euk, β
k
2
M. 4.9
Substituting4.6and4.9into4.5, we complete the proof.
In a similar way to3.7, by using the monotonicity and the assumption that 0< βk1≤
1τkβkand4.2, we obtain that for allk≥k0
Fuk1−Fu∗β
k1M−1
uk1−u∗2
M
≤1τk2
1 4ηk
2
γ2−γ
Fuk−Fu∗β
kM−1
uk−u∗2
M
−1 2γ
2−γeuk, β k
2
M.
4.10
Theorem 4.2. The sequence{uk} generated by the proposed self-adaptive inexact implicit method converges to a solution point of VVIΩ, F.
Proof. Let
ξk: 2τkτk2
4η2
k
γ2−γ 8τkη2k
γ2−γ 4τ2
kηk2
γ2−γ. 4.11
Then, it follows from4.10that for allk≥k0,
Fuk1−Fu∗β
k1M−1
uk1−u∗2
M
≤1ξkF
uk−Fu∗ β
kM−1
uk−u∗2
M
−1 2γ
2−γeuk, βk
2
M.
4.12
From the assumptions that
∞
k 0
τk<∞,
∞
k 0
ηk2<∞, 4.13
it follows that
Cs:
∞
i 0
ξi, Cp:
∞
i 0
1ξi, 4.14
are finite. The rest of the proof is similar to that ofTheorem 3.3and is thus omitted here.
5. Computational Results
In this section, we present some numerical results for the proposed self-adaptive implicit methods. Our main interests are two folds: the first one is to compare the proposed method with He’s method 11 in solving a simple nonlinear problem, showing the numerical advantage; the second one is to indicate that the strategy is rather insensitive to the initial point, the initial choice of the parameter, as well as the size of the problems. All codes were written in Matlab and run on a AMD 3200personal computer. In the following tests, the parameterβkis changed when
F
uk1−Fuk M
βkM−1uk1−uk M
>2, F
uk1−Fuk M
βkM−1uk1−uk M
< 1
That is, we setτ 1 in3.13. We setM I, and the matrix-induced norm projection is just the projection under Euclidean norm, which is very easy to implement whenΩ has some special structure. For example, whenΩis the nonnegative orthant,
{x∈ Rn|x≥0}, 5.2
then
PΩyj
⎧ ⎨ ⎩
yj, if yj ≥0,
0, otherwise; 5.3
whenΩis a box,
{x∈ Rn|l≤x≤h}, 5.4
then
PΩyj
⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩
uj, ifyj≥uj,
yj, ifuj≥yj≥lj,
lj, otherwise;
5.5
whenΩis a ball,
{x∈ Rn| x ≤r}, 5.6
then
PΩy
⎧ ⎪ ⎨ ⎪ ⎩
y, if y≤r, ry
y, otherwise. 5.7
At each iteration, we use Newton’s method25,26to solve the system of nonlinear equations
SNLE βkM−1uFu βkM−1ukF
uk−γeuk, β k
approximately; that is, we stop the iteration of Newton’s method as soon as the current iterative point satisfies4.1, and adopt it as the next iterative point, where
ηk
⎧ ⎪ ⎨ ⎪ ⎩
0.3, ifk≤kmax,
1
k−kmax, otherwise,
5.9
withkmax 50.
In our first test problem , we take
Fu arctanu AAuAc, 5.10
where the matrixAis constructed byA: WΣV. Here
W Im−2ww
ww, V In−2 vv
vv 5.11
are Householder matrices and Σ diagσi, i 1, . . . n, is a diagonal matrix with σi
cosiπ/n1. The vectorsw, v, andccontain pseudorandom numbers:
w1 13846, wi 31416wi−113846 mod 46261, i 2, . . . m,
v1 13846, vi 42108vi−113846 mod 46273, i 2, . . . n,
c1 13846, ci 45278ci−113846 mod 46219, i 2, . . . n.
5.12
The closed convex setΩin this problem is defined as
Ω: {z∈ Rm,z ≤α} 5.13
with different prescribedα. Note that in the caseAc> α,arctanu∗ AAu∗Ac α
otherwiseu∗ 0 is the trivial solution. Therefore, we test the problem withα κAcand κ∈0,1. In the test we takeγ 1.85, τk 0.85, u0 0, andβ0 0.1. The stopping criterion is
e uk, β
k
α ≤10−8. 5.14
The results inTable 1show thatβ0 0.1 is a “proper” parameter for the problem with
κ 0.05, while for the other two cases with largerκ 0.5 and with smallerκ 0.01, it is not. For any of these three cases, the method with self-adaptive strategy rule is efficient.
The second example considered here is the variant mixed complementarity problem for short VMCP, withΩ {u ∈ Rn | li ≤ uix ≤ hi, i 1, . . . , n}, where li ∈ 5,10and
hi∈1000,2000are randomly generated parameters. The mappingFis taken as
Table 1:Comparison of the proposed method and He’s method11. m 100n 50 m 500n 300
Proposed method He’s method Proposed method He’s method It. no. CPU It. no. CPU It. no. CPU It. no. CPU 0.5Ac 25 0.3910 100 1.0780 34 50.4850 — — 0.05Ac 20 0.3120 37 0.4850 25 39.8440 17 25.0940 0.01Ac 26 0.4060 350 5.8750 33 61.4070 — — “—” means iteration numbers>200 and CPU>2000sec.
Table 2:Numerical results for VMCP with dimensionn 50.
β Proposed method He’s method
It. no. CPU It. no. CPU
105 69 0.0780 — —
104 65 0.1250 7335 6.1250
103 61 0.0790 485 0.4530
102 59 0.0620 60 4.0780
10 60 0.0780 315 0.3280
1 66 0.0110 2672 2.500
10−1 70 0.0940 22541 21.0320
10−2 73 0.0780 — —
“—” means iteration numbers>3000 and CPU>300sec.
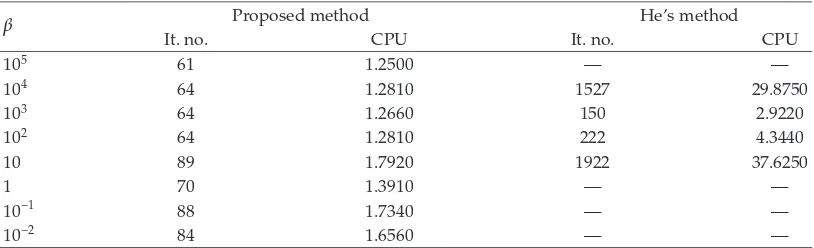
whereDuandMuqare the nonlinear part and the linear part ofFu, respectively. We form the linear partMuqsimilarly as in27. The matrixM AAB, whereAis ann×n matrix whose entries are randomly generated in the interval−5,5, and a skew-symmetric matrixBis generated in the same way. The vectorqis generated from a uniform distribution in the interval −500,0. InDu, the nonlinear part of Fu, the components are Dju aj∗arctanuj, andajis a random variable in0,1. The numerical results are summarized
in Tables2–5, where the initial iterative point isu0 0 in Tables2and3andu0 is randomly
generated in0,1in Tables4and5, respectively. The other parameters are the same:γ 1.85 andτk 0.85 fork≤40 andτk 1/kotherwise. The stopping criterion is
euk, β
k∞≤10−7. 5.16
As the results in Table 1, the results in Tables 2 to 5 indicate that the number of iterations and CPU time are rather insensitive to the initial parameterβ0, while He’s method
is efficient for proper choice ofβ. The results also show that the proposed method, as well as He’s method, is very stable and efficient to the choice of the initial pointu0.
6. Conclusions
[image:17.600.105.504.227.351.2]Table 3:Numerical results for VMCP with dimensionn 200.
β Proposed method He’s method
It. no. CPU It. no. CPU
105 82 1.6090 — —
104 74 1.4850 1434 28.3750
103 64 1.2660 199 3.8910
102 63 1.2500 174 3.4060
10 68 1.3500 1486 30.4840
1 75 1.4850 — —
10−1 75 1.5000 — —
10−2 86 1.7030 — —
[image:18.600.107.504.289.413.2]“—” means iteration numbers>3000 and CPU>300sec.
Table 4:Numerical results for VMCP with dimensionn 50.
β Proposed method He’s method
It. no. CPU It. no. CPU
105 61 0.0620 — —
104 61 0.0940 3422 3.7190
103 60 0.0790 684 0.6410
102 67 0.0780 59 0.0620
10 65 0.0940 309 0.2970
1 69 0.0940 2637 2.3750
10−1 72 0.0940 21949 18.9220
10−2 75 0.1250 — —
“—” means iteration numbers>3000 and CPU>300sec.
Table 5:Numerical results for VMCP with dimensionn 200.
β Proposed method He’s method
It. no. CPU It. no. CPU
105 61 1.2500 — —
104 64 1.2810 1527 29.8750
103 64 1.2660 150 2.9220
102 64 1.2810 222 4.3440
10 89 1.7920 1922 37.6250
1 70 1.3910 — —
10−1 88 1.7340 — —
10−2 84 1.6560 — —
“—” means iteration numbers>5000 and CPU>300sec.
[image:18.600.97.504.465.589.2]Acnowledgments
This research was supported by the NSFC Grants 10501024, 10871098, and NSF of Jiangsu Province at Grant no. BK2006214. D. Han was also supported by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry.
References
1 F. Facchinei and J. S. Pang,Finite-Dimensional Variational Inequalities and Complementarity Problems. Vol. I, Springer Series in Operations Research, Springer, New York, NY, USA, 2003.
2 F. Facchinei and J. S. Pang,Finite-Dimensional VariationalInequalities and Complementarity Problems, Vol. II, Springer Series in Operations Research, Springer, New York, NY, USA, 2003.
3 D. P. Bertsekas and E. M. Gafni, “Projection methods for variational inequalities with application to the traffic assignment problem,”Mathematical Programming Study, no. 17, pp. 139–159, 1982.
4 I. Rach ˚unkov´a and M. Tvrd ´y, “Nonlinear systems of differential inequalities and solvability of certain boundary value problems,”Journal of Inequalities and Applications, vol. 6, no. 2, pp. 199–226, 2000.
5 R. P. Agarwal, N. Elezovi´c, and J. Peˇcari´c, “On some inequalities for beta and gamma functions via some classical inequalities,”Journal of Inequalities and Applications, vol. 2005, no. 5, pp. 593–613, 2005.
6 S. Dafermos, “Traffic equilibrium and variational inequalities,”Transportation Science, vol. 14, no. 1, pp. 42–54, 1980.
7 R. U. Verma, “A class of projection-contraction methods applied to monotone variational inequali-ties,”Applied Mathematics Letters, vol. 13, no. 8, pp. 55–62, 2000.
8 R. U. Verma, “Projection methods, algorithms, and a new system of nonlinear variational inequalities,”Computers & Mathematics with Applications, vol. 41, no. 7-8, pp. 1025–1031, 2001.
9 L. C. Ceng, G. Mastroeni, and J. C. Yao, “An inexact proximal-type method for the generalized variational inequality in Banach spaces,”Journal of Inequalities and Applications, vol. 2007, Article ID 78124, 14 pages, 2007.
10 C. E. Chidume, C. O. Chidume, and B. Ali, “Approximation of fixed points of nonexpansive mappings and solutions of variational inequalities,”Journal of Inequalities and Applications, vol. 2008, Article ID 284345, 12 pages, 2008.
11 B. S. He, “Inexact implicit methods for monotone general variational inequalities,” Mathematical Programming, vol. 86, no. 1, pp. 199–217, 1999.
12 B. S. He, “A Goldstein’s type projection method for a class of variant variational inequalities,”Journal of Computational Mathematics, vol. 17, no. 4, pp. 425–434, 1999.
13 M. A. Noor, “Quasi variational inequalities,”Applied Mathematics Letters, vol. 1, no. 4, pp. 367–370, 1988.
14 J. V. Outrata and J. Zowe, “A Newton method for a class of quasi-variational inequalities,”
Computational Optimization and Applications, vol. 4, no. 1, pp. 5–21, 1995.
15 J. S. Pang and L. Q. Qi, “Nonsmooth equations: motivation and algorithms,” SIAM Journal on Optimization, vol. 3, no. 3, pp. 443–465, 1993.
16 J. S. Pang and J. C. Yao, “On a generalization of a normal map and equation,”SIAM Journal on Control and Optimization, vol. 33, no. 1, pp. 168–184, 1995.
17 M. Li and X. M. Yuan, “An improved Goldstein’s type method for a class of variant variational inequalities,”Journal of Computational and Applied Mathematics, vol. 214, no. 1, pp. 304–312, 2008.
18 B. S. He, L. Z. Liao, and S. L. Wang, “Self-adaptive operator splitting methods for monotone variational inequalities,”Numerische Mathematik, vol. 94, no. 4, pp. 715–737, 2003.
19 B. C. Eaves, “On the basic theorem of complementarity,”Mathematical Programming, vol. 1, no. 1, pp. 68–75, 1971.
20 T. Zhu and Z. Q. Yu, “A simple proof for some important properties of the projection mapping,”
Mathematical Inequalities & Applications, vol. 7, no. 3, pp. 453–456, 2004.
21 B. S. He, H. Yang, Q. Meng, and D. R. Han, “Modified Goldstein-Levitin-Polyak projection method for asymmetric strongly monotone variational inequalities,” Journal of Optimization Theory and Applications, vol. 112, no. 1, pp. 129–143, 2002.
23 D. Han, “Inexact operator splitting methods with selfadaptive strategy for variational inequality problems,”Journal of Optimization Theory and Applications, vol. 132, no. 2, pp. 227–243, 2007.
24 D. Han, W. Xu, and H. Yang, “An operator splitting method for variational inequalities with partially unknown mappings,”Numerische Mathematik, vol. 111, no. 2, pp. 207–237, 2008.
25 R. S. Dembo, S. C. Eisenstat, and T. Steihaug, “Inexact Newton methods,”SIAM Journal on Numerical Analysis, vol. 19, no. 2, pp. 400–408, 1982.
26 J. S. Pang, “Inexact Newton methods for the nonlinear complementarity problem,” Mathematical Programming, vol. 36, no. 1, pp. 54–71, 1986.
27 P. T. Harker and J. S. Pang, “A damped-Newton method for the linear complementarity problem,” in