Does Higher level of Education Reduce Poverty and Increase Inequality? Evidence from Urban India
Full text
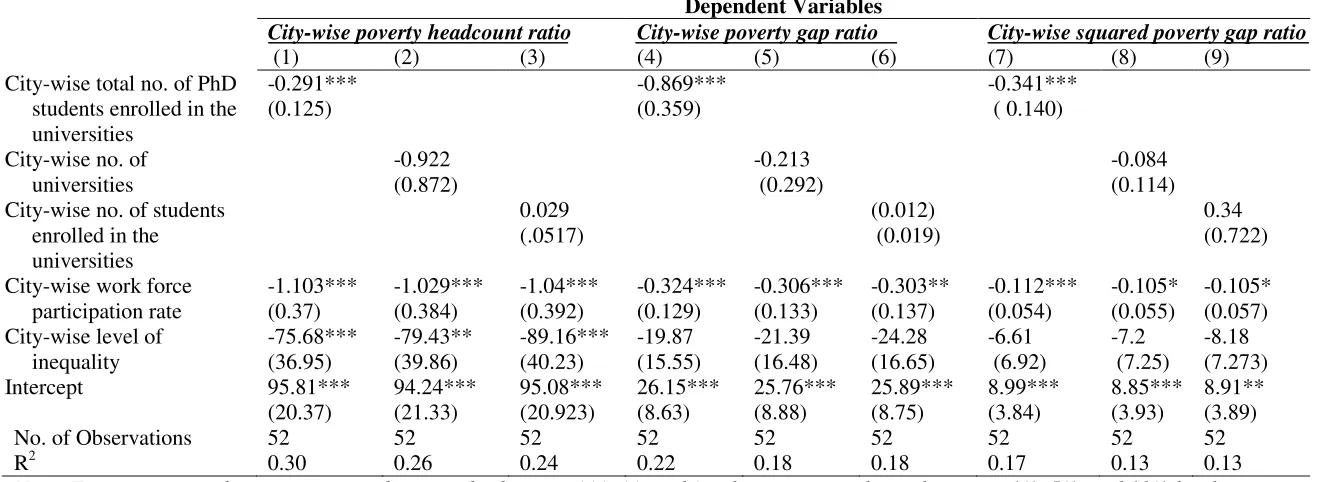
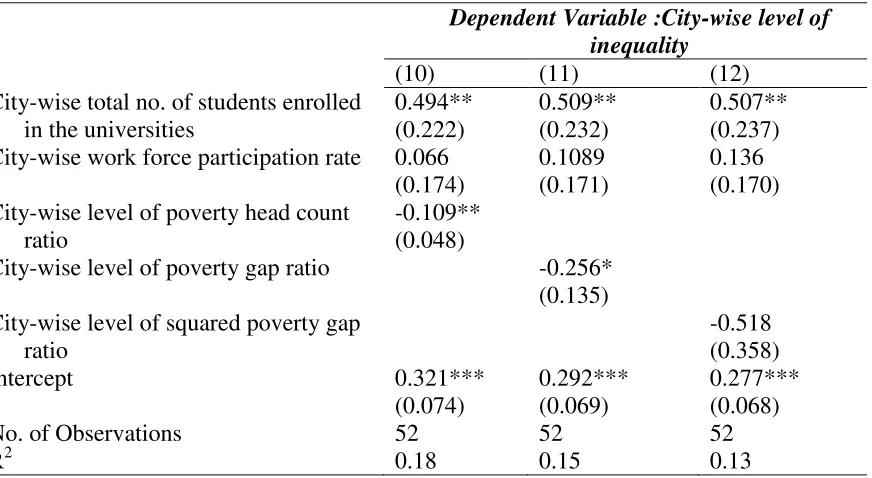
Figure
Related documents
Sekaitan dengan pemikiran ini, dipaparkan oleh Winataputra (2012) bahwa untuk mewujudkan tujuan pendidikan kewarganegaraan sebagai wahana pendidi- kan mencerdaskan
• Ache Laboratorios Farmaceuticos S.A.--We revised the outlook on the GSR and the NSR to negative from stable, and affirmed them at 'BBB-' and 'brAAA', respectively, reflecting the
See infra Part II (detailing findings of this empirical study). Huntington Nat’l Bank, No. Ohio June 20, 2011) (refusing to approve email notice for fear of forwarding); Reab v.
Inclusion of aggressive tooting and over representation of professional drivers who are more likely to experience road rage may explain the higher prevalence in our study
THERMAL ENERGY: Apart from electrical energy, the wet processing department of a textile mill requires substantial quantities of thermal energy in the form of steam as a
If you are using a Windows shared-storage location, the Service account credentials (user account name and password) must be a domain account that is configured on each
Figs 1–5. Habitus of Bruchidius species.. Head short, eyes strongly bulging, maximum head width about 1.6 times width behind eyes; eyes separated by 0.25 times head width
To quote a statement in chapter two of Communist Manifesto , “The history of ideologies proves nothing but the fact that intellectual production has always been transformed