Volume 2008, Article ID 648148,14pages doi:10.1155/2008/648148
Research Article
New Results of a Class of Two-Neuron Networks
with Time-Varying Delays
Chuangxia Huang,1Yigang He,2and Lihong Huang3
1College of Mathematics and Computers, Changsha University of Science and Technology,
Changsha, Hunan 410076, China
2College of Electrical and Information Engineering, Hunan University, Changsha, Hunan 410082, China
3College of Mathematics and Econometrics, Hunan University, Changsha, Hunan 410082, China
Correspondence should be addressed to Chuangxia Huang,cxiahuang@126.com
Received 19 September 2008; Accepted 4 December 2008
Recommended by Marta Garcia-Huidobro
With the help of the continuation theorem of the coincidence degree, a priori estimates, and differential inequalities, we make a further investigation of a class of planar systems, which is generalization of some existing neural networks under a time-varying environment. Without assuming the smoothness, monotonicity, and boundedness of the activation functions, a set of sufficient conditions is given for checking the existence of periodic solution and global exponential stability for such neural networks. The obtained results extend and improve some earlier publications.
Copyrightq2008 Chuangxia Huang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Neural networks are complex and large-scale nonlinear dynamics, while the dynamics of the delayed neural network are even richer and more complicated 1. To obtain a deep and clear understanding of the dynamics of neural networks, one of the usual ways is to investigate the delayed neural network models with two neurons, which can be described by differential systemssee2–8. It is hoped that, through discussing the dynamics of two-neuron networks, we can get some light for our understanding about the large networks. In
7, T´aboas considered the system of delay differential equations
˙
x1t −x1t αf1
x1t−τ, x2t−τ
,
˙
x2t −x2t αf2
x1t−τ, x2t−τ
, 1.1
∂f1
∂x20,0/0,
∂f2
∂x10,0/0, 1.2
and the negative feedback conditions:x2f1x1, x2>0,x2 /0;x1f2x1, x2<0,x1 /0. T´aboas
showed that there is anα0>0 such that forα > α0, there exists a nonconstant periodic solution
with period greater than 4. Further study on the global existence of periodic solutions to system1.1can be found in2,3. All together there is only one delay appearing in both equations. Ruan and Wei6investigated the existence of nonconstant periodic solutions of the following planar system with two delays
˙
x1t −a0x1t a1f1
x1t−τ1, x2t−τ2
,
˙
x2t −b0x2t b1f2
x1t−τ1, x2t−τ2
, 1.3
wherea0 > 0, b0 > 0,a1 andb1 are constants, the functionsf1 andf2 satisfyfj ∈ C3R2, fj0,0 0,∂fj/∂xj0,0 0,j 1,2;x2f1x1, x2/0 forx2 /0;x1f2x1, x2/0 forx1 /0; ∂f1/∂x20,0/0,∂f2/∂x10,0/0.
Recently, Chen and Wu9considered the following system:
˙
xt −μ1xt F
yt−τ1
I1,
˙
yt −μ2yt−G
xt−τ2
I2,
1.4
whereμ1andμ2are positive constants,τ1andτ2are nonnegative constants withτ :τ1 τ2>
0,I1andI2are constants, andFandGare boundedC1-functions with ˙Ft>0, and ˙Gt>0
fort ∈ R. By discussing a two-dimensional unstable manifold of the transformation of the system1.4, they got some results about slowly oscillating periodic solutions.
However, delays considered in all above systems1.1–1.4are constants. It is well known that the delays in artificial neural networks are usually time-varying, and they sometime vary violently with time due to the finite switching speed of amplifiers and faults in the electrical circuit. They slow down the transmission rate and tend to introduce some degree of instability in circuits. Therefore, fast response must be required in practical artificial neural-network designs. As pointed out by Gopalsamy and Sariyasa10,11, it would be of great interest to study the neural networks in periodic environments. On the other hand, drop the assumptions of continuous first derivative, monotonicity, and boundedness for the activation might be better candidates for some purposes, see 12. Motivated by above mentioned, in this paper, we continue to consider the following planar system:
˙
x1t −a1tx1t b1tf1
x1
t−τ11t
, x2
t−τ12t
I1t,
˙
x2t −a2tx2t b2tf2
x1
t−τ21t
, x2
t−τ22t
I2t,
1.5
whereait∈CR,0,∞,bit, Iit∈CR, R, i1,2, are periodic with a common period ω>0,fi·,·∈CR2, R,τijt∈CR,0,∞, i,j1,2 beingω-periodic.
functions, a family of sufficient conditions are given for checking the existence of periodic solution and global exponential stability for such neural networks. Our results extend and improve some earlier publications. The remainder of this article is organized as follows. In
Section 2, the basic notations and assumptions are introduced. After giving the criteria for checking the existence of periodic solution and global exponential stability for the neuron networks in Section 3, one illustrative example and simulations are given inSection 4. We also conclude this paper inSection 5.
2. Preliminaries
In this section, we state some notations, definitions, and lemmas. Assume that nonlinear system1.5is supplemented with initial values of the type
uit φit, −τ ≤t≤0, τ max 1≤i,j≤2
τijt
, 2.1
in whichφit, i1,2 are continuous functions. Setφ φ1, φ2, φ3T, ifx∗t x1∗t, x∗2tT
is a solution of system1.5, then we denote
φ−x∗2
i1
sup
−τ≤t≤0
φit−x∗
it. 2.2
Definition 2.1. The solutionx∗t x∗1t, x2∗tT is said to be globally exponentially stable, if there existλ >0 andm≥1 such that for any solutionxt x1t, x2tT of1.5, one has
xit−x∗
it≤mφ−x∗e−λt fort≥0, 2.3
whereλis called to be globally exponentially convergent rate.
To establish the main results of the model1.5, some of the following assumptions will be applied:
H1|fix1, x2| ≤ αi|x1| βi|x2| Mi for allx1, x2T ∈R2, i 1,2, whereαi ≥ 0, βi ≥
0, Mi>0 are constants;
H2there exist constantsαi ≥0, βi ≥ 0,such that|fjx1, x2−fjy1, y2| ≤αi|x1−y1| βi|x2−y2|for anyx1, x2T ∈R2, y1, y2T ∈R2.
ForV ∈Ca, ∞, R, one denotes
D−Vt lim sup
h→0−
Vt h−Vt
h ,
D−Vt lim inf
h→0−
Vt h−Vt
h .
2.4
Consider an abstract equation in a Branch space X In this section, we use the coincidence degree theory to obtain the existence of anω-periodic solution to1.5. For the sake of convenience, we briefly summarize the theory as below.
LetXandZbe normed spaces,L: DomL⊂X →Zbe a linear mapping, andN:X → Zbe a continuous mapping. The mappingLwill be called a Fredholm mapping of index zero if dim KerLcodim ImL <∞and ImLis closed inZ. IfLis a Fredholm mapping of index zero, then there exist continuous projectorsP:X →XandQ:Z →Zsuch that ImP KerL
and ImLKerQImI−Q. It follows thatL|DomL∩KerP:I−PX →ImLis invertible. We denote the inverse of this map byKp. IfΩis a bounded open subset ofX, the mappingN
is calledL-compact onΩifQNΩis bounded andKpI−QN:Ω →Xis compact. Because
ImQis isomorphic to KerL, there exists an isomorphismJ: ImQ →KerL.
LetΩ⊂Rnbe open and bounded,f ∈C1Ω, Rn∩CΩ, Rnandy∈Rn\f∂Ω∪S f,
that is,yis a regular value off. Here,Sf {x∈Ω:Jfx 0}, the critical set off, andJf is
the Jacobian offatx. Then, the degree deg{f,Ω, y}is defined by
deg{f,Ω, y} x∈f−1y
sgnJfx, 2.5
with the agreement that the above sum is zero iff−1y ∅. For more details about the
degree theory, one refers to the book of Deimling14.
Now, with the above notation, we are ready to state the continuation theorem.
Lemma 2.2Continuation theorem13, page 40. LetLbe a Fredholm mapping of index zero and
letNbeL-compact onΩ. Suppose that
afor eachλ∈0,1, every solutionxofLxλNxis such thatx/∈∂Ω; bQNx /0for eachx∈∂Ω∩KerLand
degJQN, Ω∩KerL, 0/0. 2.6
Then, the equationLx Nx has at least one solution lying inDomL∩Ω. For more details about degree theory, we refer to the book by Deimling [14].
For the simplicity of presentation, in the remaining part of this paper, we also introduce the following notation:
aimin
ait
, bijmaxbijt, IimaxIit,
Da1−b1α1 −b1β1 −b2α2 a2−b2β2
,
D1
I1 b1M1 −b1β1 I2 b2M2 a2−b2β2
, D2
a1−b1α1 I1 b1M1 −b2α2 I2 b2M2 .
3. Main results
Theorem 3.1. SupposeH1holds andD1/D >0,D2/D > 0, then system1.5has aω-periodic
solution.
Proof. TakeX{ut x1t, x2tT ∈CR, R2:ut ut ωfort∈R}and denote
|xi| max
t∈0,ω|xit|, i1,2; u0maxi1,2|xi|. 3.1
Equipped with the norm·0,Xis a Banach space. For anyut∈X, because of the periodicity, it is easy to check that
t −→ −a1txt b1tf1
xt−τ11t
, yt−τ12t
I1t −a2tyt b2tf2
xt−τ21t
, yt−τ22t
I2t
∈X. 3.2
Let
L: DomLu∈X:u∈C1R, R2u −→u∈X,
P :Xu −→u∈X, Q:X x −→x∈X, 3.3
where for anyγ γ1, γ2T ∈R2, we identify it as the constant function inXwith the value
vectorγ γ1, γ2T. DefineN:X →Xgiven by
Nut −a1tx1t b1tf1
x1
t−τ11t
, x2
t−τ12t
I1t −a2tx2t b2tf2
x1
t−τ21t
, x2
t−τ22t
I2t
∈X. 3.4
Then, system1.5can be reduced to the operator equationLuNu. It is easy to see that
KerLR2,
ImL{x∈X :x0}, which is closed inX,
dim KerLcodim ImL2<∞,
3.5
andP,Qare continuous projectors such that
ImP KerL, KerQImLImI−Q. 3.6
It follows thatLis a Fredholm mapping of index zero. Furthermore, the generalized inverse
toLKp: ImL →KerP∩DomLis given by
Kpu
t
⎛ ⎜ ⎜ ⎜ ⎜ ⎝
t
0
x1sds− 1 ω
ω
0
s
0
x1vdvds
t
0
x2sds−
1
ω
ω
0
s
0
x2vdvds ⎞ ⎟ ⎟ ⎟ ⎟
Thus, QNut ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ 1 ω ω 0
−a1sx1s b1sf1
x1
s−τ11s
, x2
s−τ12s
I1s ds 1 ω ω 0
−a2sx2s b2sf2
x1
s−τ21s
, x2
s−τ22s
I2s ds ⎞ ⎟ ⎟ ⎟ ⎟ ⎠,
KpI−QNu t ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ t 0
−a1sx1s b1sf1
x1
s−τ11s
, x2
s−τ12s
I1s
ds
t
0
−a2sx2s b2sf2
x1
s−τ21s
, x2
s−τ22s
I2s ds ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ − ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ 1 ω ω 0 s 0
−a1vx1v b1vf1
x1
v−τ11v
, x2
v−τ12v
I1v
dvds
1 ω ω 0 s 0
−a2vx2v b2vf2
x1
v−τ21v
, x2
v−τ22v
I2v
dvds
⎞ ⎟ ⎟ ⎟ ⎟ ⎠ ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ 1 2− t ω ω 0
−a1sx1s b1sf1
x1
s−τ11s
, x2
s−τ12s
I1s ds 1 2− t ω ω 0
−a2sx2s b2sf2
x1
s−τ21s
, x2
s−τ22s
I2s ds ⎞ ⎟ ⎟ ⎟ ⎟ ⎠. 3.8
Clearly,QNandKpI−QNare continuous. For any bounded open subsetΩ⊂X,QNΩ
is obviously bounded. Moreover, applying the Arzela-Ascoli theorem, one can easily show thatKpI−QNΩis compact. Note thatKpI−QNis a compact operator and QNΩ
is bounded, therefore,N isL-compact onΩ with any bounded open subsetΩ ⊂ X. Since ImQ KerL, we take the isomorphismJ of ImQ onto KerL to be the identity mapping. Corresponding to equationLuλNu, λ∈0,1, we have
˙
x1t λ
−a1tx1t b1tf1
x1t−τ11t
, x2t−τ12t
I1t
,
˙
x2t λ
−a2tx2t b2tf2
x1
t−τ21t
, x2
t−τ22t
I2t
. 3.9
Now we reach the position to search for an appropriate open bounded subset Ω for the application of the Lemma 2.2. Assume that u ut ∈ X is a solution of system 3.9 for someλ ∈0,1. Then, the componentsxit i 1,2ofutare continuously differentiable.
Thus, there existsti∈0, ωsuch that|xiti|maxt∈0,ω|xit|. Hence, ˙xiti 0. This implies
a1 t1 x1
t1b1 t1 f1 x1
t1−τ1
t1
, x2
t1−τ2
t1
I1
t1,
a2
t2
x2
t2b2 t2 f2 x1
t2−τ3
t2
, x2
t2−τ4
t2
I1
t2.
Since
fi
x1, x2≤αix1 βix2 Mi fori1,2, 3.11
we get
x1
t1≤
α1b1x1
t1−τ11
t1 a1
β1b1x2
t1−τ12
t1 a1
b1M1 I1 a1
,
x2
t2≤
α2b2x1
t2−τ21
t2 a2
β2b2x2
t2−τ22
t2 a2
b2M2 I2 a2
.
3.12
Setk1D1/D,k2D2/D, we find that
k1 α1b1
a1 k1 β1b1
a1 k2
b1M1 I1 a1 ,
k2 α2b2
a2 k1
β2b2 a2
k2
b2M2 I2 a2
.
3.13
Now, we choose a constant numberd >1 and take
Ω x1, x2
T ∈
R2; xi< dki fori1,2
, 3.14
wherek1D1/D >0,k2D2/D >0. We will show thatΩsatisfies all the requirements given
inLemma 2.2. In fact, we will prove that ifxit−τijt∈Ωthenxit∈Ωfori, j 1,2, t≥0.
Therefore, it means that u utis uniformly bounded with respect toλ when the initial value function belongs toΩ. It follows from3.12and3.13that
xi αibi ai
x1
ti−τi1t βibi
ai
x1
ti−τi2t biMi Ii ai
≤ αibi ai dk1
βibi ai dk2
biMi Ii ai < d
α
ibi ai k1
βibi ai k2
biMi Ii ai
,
3.15
i1,2. Therefore,
xi
0< dki fori1,2. 3.16
Clearly,dki,i 1,2 are independent of λ. It is easy to see that there are noλ ∈ 0,1and u ∈ ∂Ωsuch thatLu λNu. Ifu x1, x2T ∈ ∂Ω∩KerL ∂Ω∩R2, thenuis a constant
vector inR2with|xi|dk
ifori1,2. Note thatQNuJQNu, we have
QNu ⎛ ⎜ ⎜ ⎜ ⎜ ⎝
−x11 ω
ω
0
a1tdt f1
x1, x2
1
ω
ω
0
b1tdt 1 ω
ω
0 I1tdt
−x2
1
ω
ω
0
a2tdt f2
x1, x2
1
ω
ω
0 b2tdt
1
ω
ω
0 I2tdt
⎞ ⎟ ⎟ ⎟ ⎟
We claim that
QNu
i>0 u∈∂Ω∩KerL∂Ω∩R3, i1,2. 3.18
Contrarily, suppose that there exists someisuch that|QNui|0, that is,
xi
1
ω
ω
0
aitdtfi
x1, x2
1
ω
ω
0 bitdt
1
ω
ω
0
Iitdt. 3.19
So, we have
dki|xi| ≤
1
ai
fi
x1, x2
1
ω
ω
0 bitdt
1
ω
ω
0 Iitdt
≤ αibi ai
dk1 βibi
ai dk2
biMi Ii ai
< d
αibi ai
k1 βibi
ai k2
biMi Ii ai
dki,
3.20
this is a contradiction. Therefore,3.17holds, and hence,
QNu /0, for any u∈∂Ω∩KerL∂Ω∩R2. 3.21
Now, consider the homotopyF:Ω∩KerL×0,1 → Ω∩KerL, defined by
Fu, μ −μdiag
1
ω
ω
0
a1tdt,
1
ω
ω
0 a2tdt
u 1−μQNu, 3.22
whereu∈Ω∩KerL Ω∩R2andμ∈0,1. Whenu∈∂Ω∩KerL∂Ω∩R2andμ∈0,1, u x1, x2Tis a constant vector inR2with|xi|dkifori1,2. Thus
Fu, μ
0maxi1,2
−xi1
ω
ω
0
aitdt 1−μfi
x1, x2
1
ω
ω
0 bitdt
. 3.23
We claim that
Fu, μ/ 0 u, μ∈∂Ω∩KerL×0,1. 3.24
Contrarily, suppose thatFu, μ00, then,
xi
1
ω
ω
0
aitdt 1−μfi
x1, x2
1
ω
ω
0
Thus,
dki|xi| ≤
1−μ
ai bifi
x1, x2
< d
αibi ai
k1 βibi
ai
k2 biMi Ii ai
dki. 3.26
This is impossible. Thus,3.22holds. From the property of invariance under a homotopy, it follows that
degJQN,Ω∩KerL,0
degF·,0,Ω∩KerL,0
degF·,1,Ω∩KerL,0
sgn
−1 ω
ω
0
a1tdt 0
0 −1
ω
ω
0 a2tdt
sgn
1
ω
ω
0 a1tdt
1
ω
ω
0 a2tdt
/ 0.
3.27
We have shown thatΩsatisfies all the assumptions of Lemma 2.2. Hence, Lu Nuhas at least oneω-periodic solution on DomL∩Ω. This completes the proof.
Corollary 3.2. Suppose that there exist positive constantsMisuch that|fix1, x2| ≤Mifori1,2.
Then system1.5has at least anω-periodic solution.
Proof. As|fix1, x2| ≤Mii1,2,implies thatαi, βi 0, hence, the conditions in Theorem
2.1 are all satisfied.
Remark 3.3. From Corollary 3.2, we can find that the conditionai > bi in4, Theorem 2.1
can be dropped out. Therefore, Theorem 3.1is greatly generalized results to 4, Theorem 2.1. Furthermore, we should point out that theTheorem 3.1is different from the the existing work in5when without assuming the boundedness, monotonicity, and differentiability of activation functions. In fact, the explicit presence ofωin Theorem 2.1see5may impose a very strict constraint on the coefficients of1.5 e.g., whenωis very large or small. Since our results are presented independent ofω, it is more convenient to design a neural network with delays.
Theorem 3.4. Suppose thatfi, i1,2satisfy the hypothesesH2. IfD1/D >0,D2/D >0, then
system1.5has exactly one periodic solutionxt . Moreover, it is globally exponentially stable.
Proof. From H2, we can conclude H1 is true. It is obvious that all the hypotheses in
Theorem 2.1 hold withMi |fi0,0|, i 1,2.Thus, system1.5has at least one periodic
calculation of the upper left derivative of|xit−xit|along the solutions of system1.5
leads to
D xit−xit
D−sgnxit−xit
xit−xit
≤ −aitx1t−x1t bit ×fi
x1
t−τi1t
,x2
t−τi2t
−fi
x1
t−τi1t
, x2
t−τi2t ≤ −aitx1t−x1t bit
×αix1
t−τi1t
−x1
t−τi1t βix2
t−τi2t
−x2
t−τi2t,
3.28
whereD−denotes the upper left derivative,i1,2. Letzit |xit−xit|. Then,3.27can
be transformed into
D−zit≤ −aizit biαi sup t−τ≤s≤t
z1s biβi sup t−τ≤s≤t
z2s. 3.29
FromD1/D >0,D2/D >0 and3.13, we have
k1> b1α1
a1 k1 b1β1
a1 k2,
k2> b2α2
a2 k1
b2β2 a2
k2.
3.30
Then, there exists a constantσ >0 such that
−k1a1 k1b1α1 k2b1β1< σ, −k2a2 k1b2α2 k2b2β2< σ.
3.31
Thus, we can choose a constant 0< λ1 such that
λki
−kiai
k1biαi k2biβi
eλτ<0, i1,2. 3.32
Now, we choose a constantN1 such that
Nkie−λt>1, ∀t∈−τ,0, i1,2. 3.33
Set
Yit Nki
sup
−τ≤s≤0
z1s sup
−τ≤s≤0
z2s ε
for∀ε >0. From3.32and3.34, we obtain
D−Yit>
−kiai
k1biαi k2biβi
eλτN
2
j1
sup
−τ≤s≤0
zjs ε
e−λt
−aiYit biαi sup t−τ≤s≤t
Y1s biβi sup t−τ≤s≤t
Y2s.
3.35
In view of3.33and3.34, we have
Yit > 2
j1
sup
−τ≤s≤0
zjs ε > zit, ∀t∈−τ,0. 3.36
We claim that
zit< Yit, ∀t >0, i1,2. 3.37
Contrarily, there must existi∈ {1,2}andti>0 such that
ziti Yiti, zit< Yit ∀t∈−τ, ti, i1,2. 3.38
It follows that
0≤D−zi
ti
−Yi
ti
≤lim sup
h→0−
zi
ti h
−zi
ti
h −lim infh→0−
Yi
ti h
−Yi
ti
h
D−zi
ti
−D−Yi
ti
.
3.39
From3.29,3.35, and3.38, we obtain
D−zi
ti
≤ −aizi
ti
biαi sup ti−τ≤s≤ti
z1s biβi sup ti−τ≤s≤ti
z2s< D−Yi
ti
, 3.40
which contradicts3.39. Hence,3.37holds. Lettingε → 0 andm max1≤i≤2{Nki 1},
from3.34and3.37, we have
xit−xitzit≤Nki
2
j1
sup
−τ≤s≤0
zjs ε
e−λt
≤mφ−xe−λt, fort≥0, i1,2.
3.41
0 50 100 150 Timet
−0.6
−0.4
−0.2
0 0.2 0.4 0.6 0.8 1 1.2 1.4
Solution
x1
,x
[image:12.600.184.415.95.278.2]2
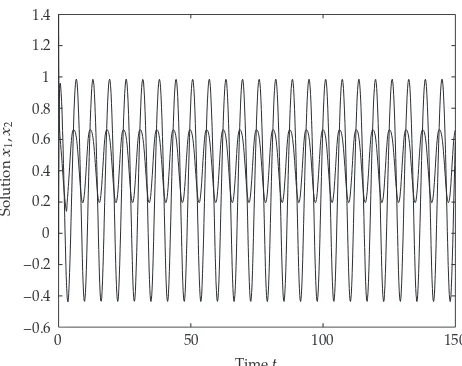
Figure 1:Numerical solutionx1t, x2tof system4.1, whereτ11t 5, τ12t 2, τ21t 3, τ22t 6,
x1s −0.2, x2s 1.4 fors∈−6,0.
Remark 3.5. From Theorem 3.4, it is easy to see that our results independent ofω and τ, we have dropped out the condition b of Theorem 3.1 in 4 and the condition: ai > αi βi|bi|ea
∗
iτ of Theorem 3.1 in5. Therefore, it is generalized the corresponding results
in4,5.
4. Example and numerical simulation
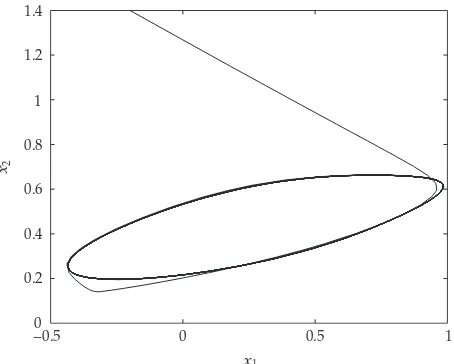
In this section, we will give a example to illustrate our results. Using the method of numerical simulation in15, we will find that the theoretical conclusions are in excellent agreement with the numerically observed behavior.
Example 4.1. Consider a two-neuron networks with delays as follows:
˙
x1t −a1tx1t b1tf1
x1t−τ11t
, x2
t−τ12t
I1t,
˙
x2t −a2tx2t b2tf2
x1
t−τ21t
, x2
t−τ22t
I2t,
4.1
wherea1t 49/8 cos t,a2t 15/2 sint,b1t 1 2 cost,b2t 1−sint,I1t sint, I2t 2 cost,f1x1, x2 cos1/4x1 1/8|x1| sinx2−1/2|x2| 1,f2x1, x2 sinx1− 1/4x1 cos1/2x2 1/4|x2| 2, and 0 ≤ τijt < ∞ are any 2π-periodic continuous
functions fori, j1,2.
Obviously, the requirements of smoothness, monotonicity, and boundedness on the activation functions are relaxed in our model. By some simple calculations, we obtainα1
−0.5 0 0.5 1
x1
0 0.2 0.4 0.6 0.8 1 1.2 1.4
[image:13.600.187.414.97.279.2]x2
Figure 2:Phase trajectories of system4.1.
5. Conclusion
In this paper, we have derived sufficient algebraic conditions in terms of the parameters of the connection and activation functions for periodic solutions and global exponential stability of a two-neuron networks with time-varying delays. The obtained results extend and improve some earlier publications, which are all independent of the delays and the periodωand may be highly important significance in some applied fields.
Acknowledgments
This work was supported in part by the High-Tech Research and Development Program of China under Grant no. 2006AA04A104, China Postdoctoral Science Foundation under Grants no. 20070410300 and no. 200801336, the Foundation of Chinese Society for Electrical Engineering, and the Hunan Provincial Natural Science Foundation of China under Grant no. 07JJ4001.
References
1 J. Wu,Introduction to Neural Dynamics and Signal Transmission Delay, vol. 6 ofde Gruyter Series in Nonlinear Analysis and Applications, Walter de Gruyter, Berlin, Germany, 2001.
2 M. Z. Baptistini and P. Z. T´aboas, “On the existence and global bifurcation of periodic solutions to planar differential delay equations,”Journal of Differential Equations, vol. 127, no. 2, pp. 391–425, 1996.
3 S. M. S. Godoy and J. G. dos Reis, “Stability and existence of periodic solutions of a functional differential equation,”Journal of Mathematical Analysis and Applications, vol. 198, no. 2, pp. 381–398, 1996.
4 C. Huang and L. Huang, “Existence and global exponential stability of periodic solution of two-neuron networks with time-varying delays,”Applied Mathematics Letters, vol. 19, no. 2, pp. 126–134, 2006.
5 C. Huang, L. Huang, and T. Yi, “Dynamics analysis of a class of planar systems with time-varying delays,”Nonlinear Analysis: Real World Applications, vol. 7, no. 5, pp. 1233–1242, 2006.
7 P. T´aboas, “Periodic solutions of a planar delay equation,”Proceedings of the Royal Society of Edinburgh. Section A, vol. 116, no. 1-2, pp. 85–101, 1990.
8 K. Liu and G. Yang, “Strict stability criteria for impulsive functional differential systems,”Journal of Inequalities and Applications, vol. 2008, Article ID 243863, 8 pages, 2008.
9 Y. Chen and J. Wu, “Slowly oscillating periodic solutions for a delayed frustrated network of two neurons,”Journal of Mathematical Analysis and Applications, vol. 259, no. 1, pp. 188–208, 2001.
10 K. Gopalsamy and S. Sariyasa, “Time delays and stimulus-dependent pattern formation in periodic environments in isolated neurons,”IEEE Transactions on Neural Networks, vol. 13, no. 3, pp. 551–563, 2002.
11 K. Gopalsamy and S. Sariyasa, “Time delays and stimulus dependent pattern formation in periodic environments in isolated neurons—II,”Dynamics of Continuous, Discrete & Impulsive Systems. Series B, vol. 9, no. 1, pp. 39–58, 2002.
12 M. Forti and A. Tesi, “New conditions for global stability of neural networks with application to linear and quadratic programming problems,”IEEE Transactions on Circuits and Systems. I, vol. 42, no. 7, pp. 354–366, 1995.
13 R. E. Gaines and J. L. Mawhin,Coincidence Degree, and Nonlinear Differential Equations, vol. 568 of Lecture Notes in Mathematics, Springer, Berlin, Germany, 1977.
14 K. Deimling,Nonlinear Functional Analysis, Springer, Berlin, Germany, 1985.