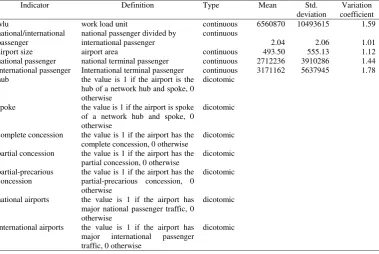
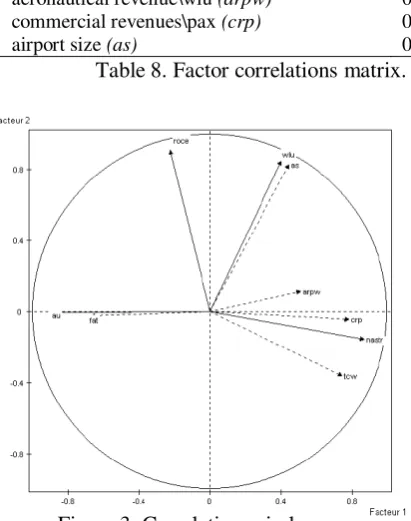
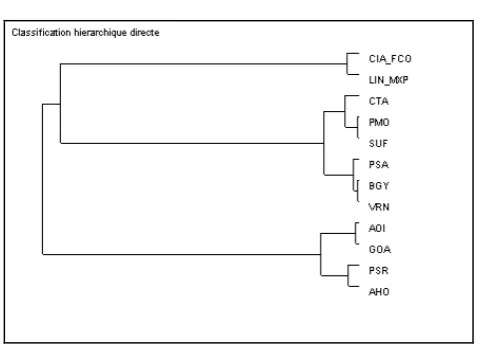
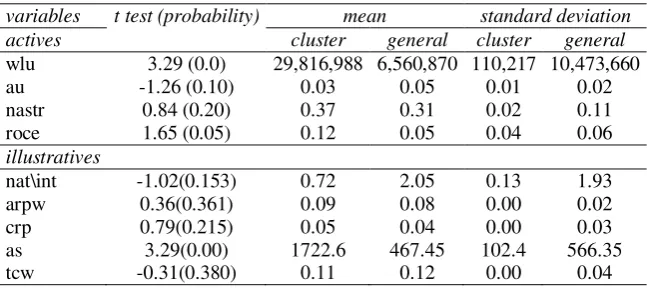
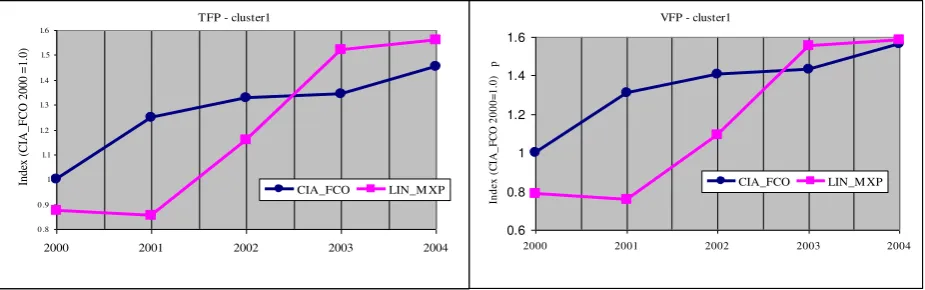
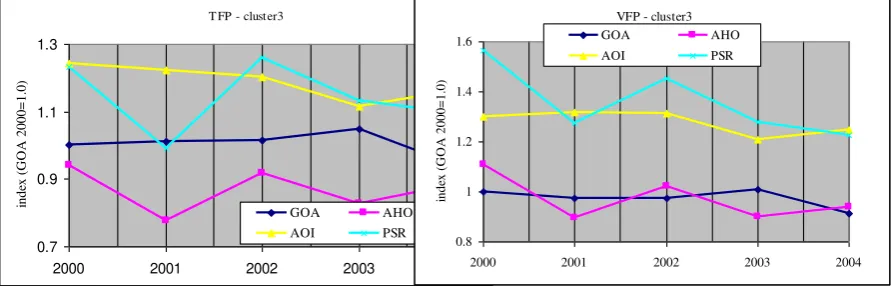
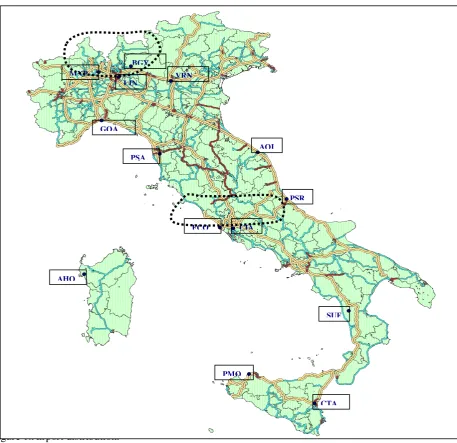
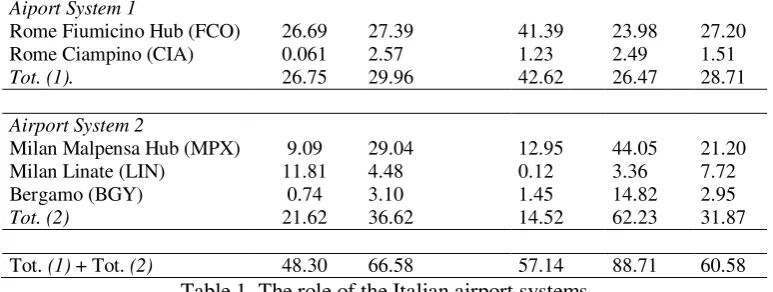
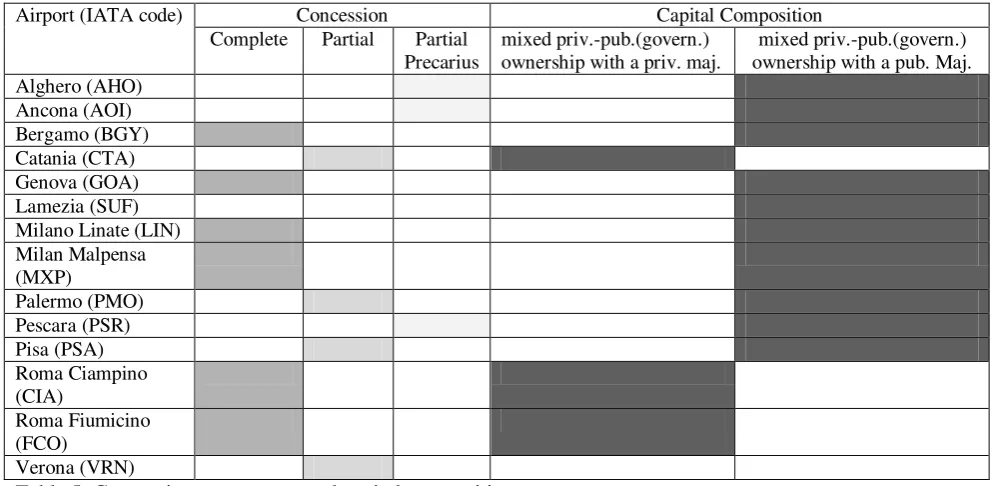
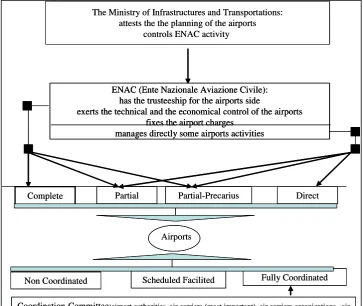
The performance of Italian airports
Full text
Figure
Related documents
Today the fact is that very few people can distinguish between a good diamond and a bad even know if what they are looking is a diamond at all or not. Diamonds are known by its 4
Apply discount rate to lost earning capacity damages for each year to calculate annual present value of that year. – For past and current years discount factor is 1.0 – For
National Conference on Technical Vocational Education, Training and Skills Development: A Roadmap for Empowerment (Dec. 2008): Ministry of Human Resource Development, Department
NAM FHo?AIIAI HKn =I JDA I=mA KIAH =I JDA FHo?AII MDE?D ?HA=JA@ JDAm. 6DEI EI @onA >O HKnnEnC =n =KJDAnJE?=JEon FHoJo?ol MEJD factotum Jo FHoLA JD=J JDA FHo?AII D=I =??AII Jo
Монгол гүүний саалийн хугацаанд (6-10-р саруудад) саамны гарц, найрлага түүний физик- химийн үзүүлэлт, хадгалалтын нөхцөл саамны шинэлэг байдалд хэрхэн
Linux, however, does provide a kernel option starting with the 3.10 kernel to disable the timer tick on processors running a single task.. Disabling Timer