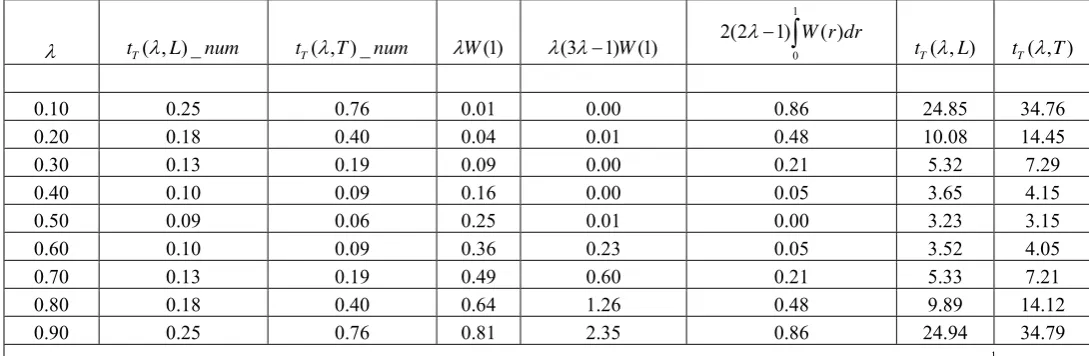
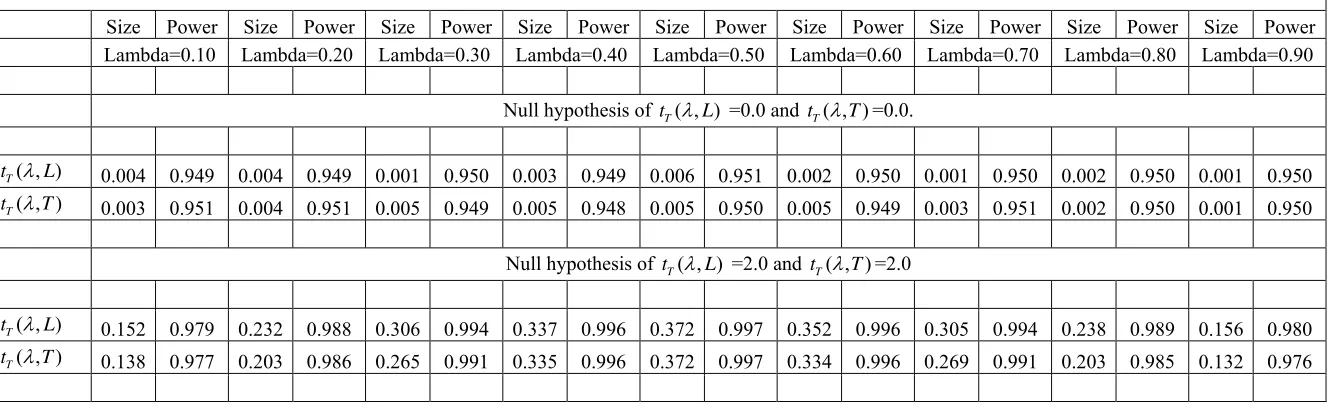
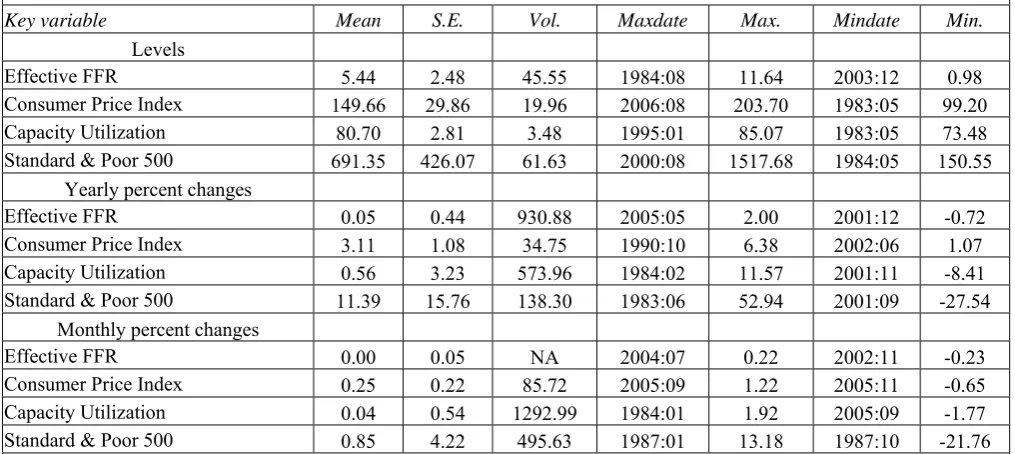
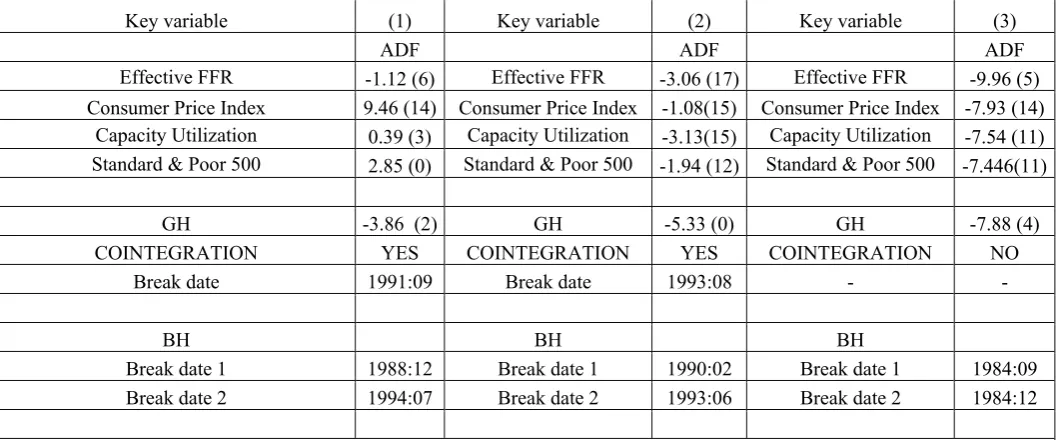
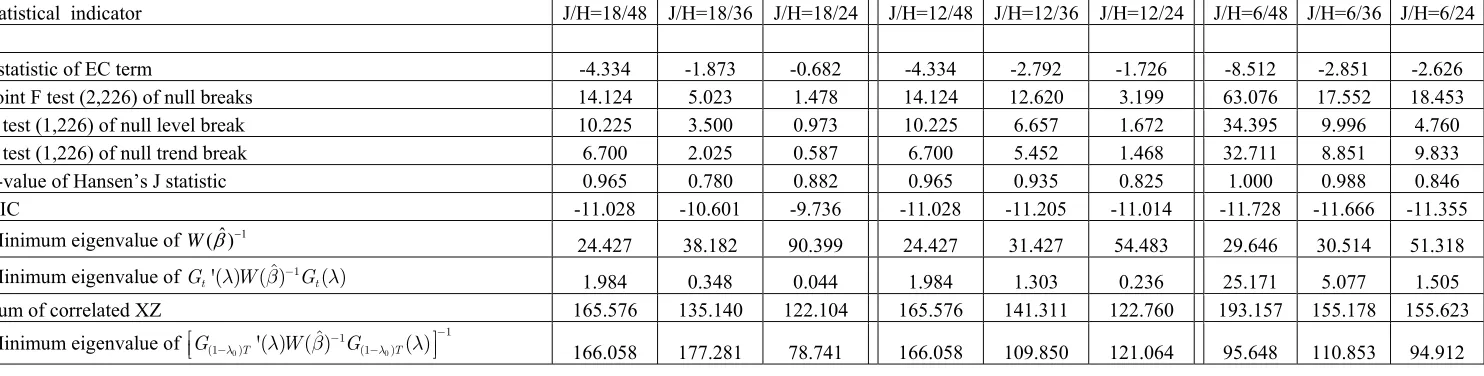
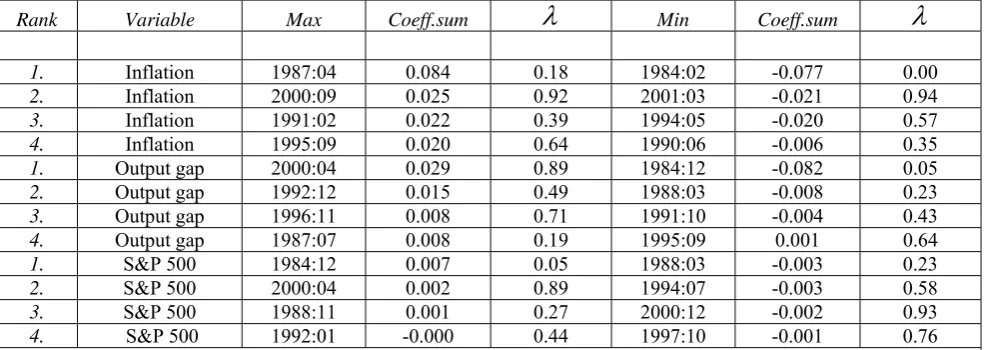
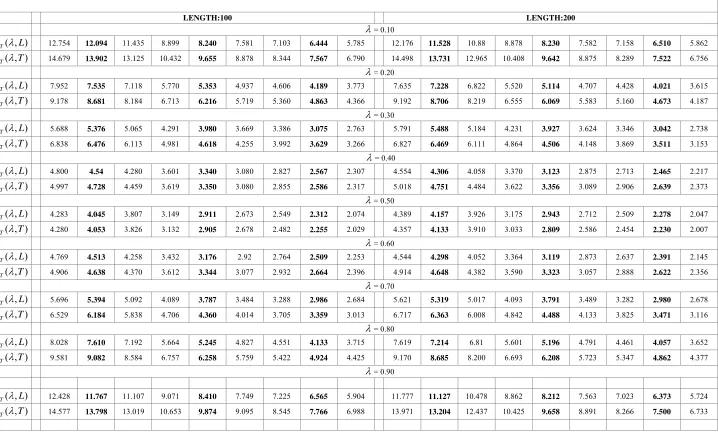
The U S Dynamic Taylor Rule With Multiple Breaks, 1984 2001
Full text
Figure
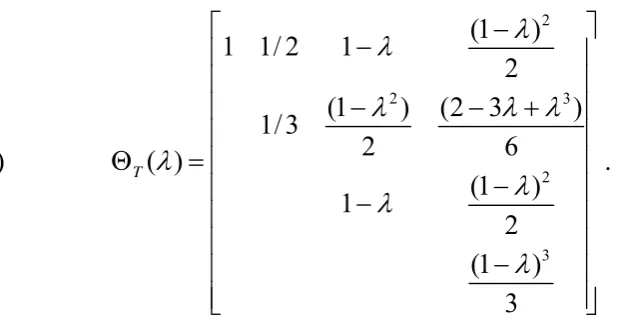

Related documents
We discuss a case of a patient with a benign cystic parathyroid adenoma presenting in sinister fashion with, in particular, a massively raised serum PTH level only previously seen
This Honors Thesis is brought to you for free and open access by the Honors Program at Digital Commons @ Loyola Marymount University and Loyola Law School.. It has been accepted
2-piece brackets are for mounting Burle cameras, and the round bracket with 4-3/4” bolt circle is for mounting COHU
The Ontario Electrical Safety Code and Ontario Regulation 438/07 recognize certification organizations accredited by the Standards Council of Canada to approve electrical
Can a woman who cannot use combined (oestrogen-progestin) oral contraceptives or progestin-only pills as an ongoing method still safely use ECPs?... This is because ECP treatment
I certify that an Examination Committee met on 18 August 2010 to conduct the final examination of Nalini d/o Arumugam on the Doctor of Philosophy thesis entitled “Examining
For this virtual higher education proposal to be sustainable and for it to meet the mentioned needs of a knowledge society in Latin America at a time of global ambiguity and need
The fragile deposit structure allows persistent relationship building to be delegated to the banker (much as in Diamond [1984] where the intermediary monitors on behalf of