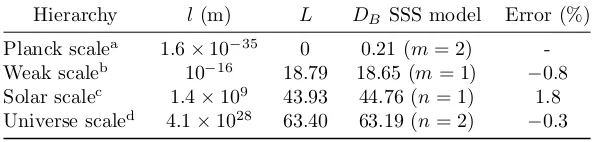
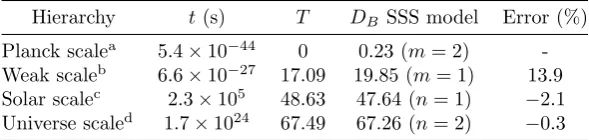
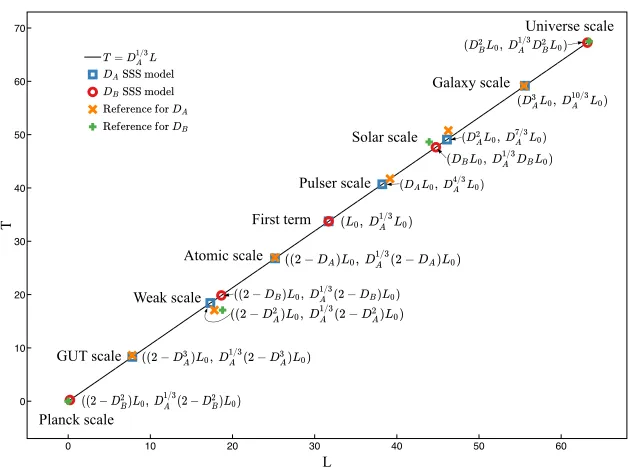
Cosmological constant decaying with CMB temperature
Full text
Figure
Related documents
Cite this article as: Cheng et al.: Weak up-regulation of serum response factor in gastric ulcers in patients with co-morbidities is associated with increased risk of
Background: Councils of Chiropractic Education (CCE) indirectly influence patient care and safety through their role of ensuring the standards of training delivered by
This study aimed to assess the prevalence of anxiety and depression and to identify their associated factors including metabolic components among people with type 2 diabetes..
We compared NOSM UGs and PGs with the full popula- tion of College of Family Physicians of Canada (CFPC)- certified physicians who completed UG education at a Canadian medical
An oxidation resistant Re and Ru containing alloy, meeting specified creep life at (i) minimum density, (ii) minimum cost. Any success depends upon accuracy of underlying
Pertaining to the secondary hypothesis, part 1, whether citalopram administration could raise ACTH levels in both alcohol-dependent patients and controls, no significant
(1999–2000), we examined trajectories of 50 prominence eruptions in order to address how prominence motions affect or reflect the surrounding coronal structures. We marked
pattern is closely linked to the higher synoptic cyclone activity over the central Arctic Ocean