Applications of tensor in various scientific and mathematical fields
Full text
Figure
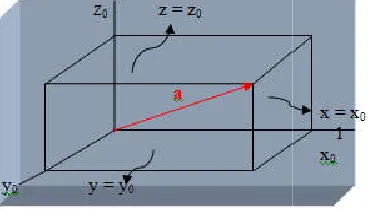
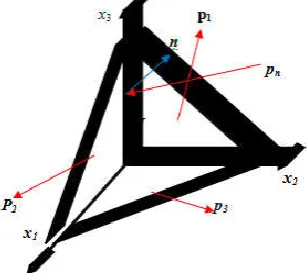
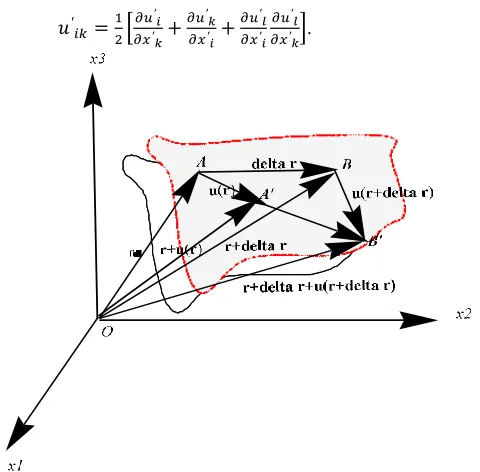
Related documents
Selected candidates will be included on a reserve list and, depending on the availability of Temporary Agent posts and the budgetary situation, may be offered a five-year renewable
accession process has significantly triggered political reforms in Turkey and brought about substantial constitutional and legal amendments particularly in the areas in relation to
The prevalence of obesity, hypertension, prediabetes, alcohol consump- tion, immigration and urbanization increased during the study period and the consumption of fruits and vegetables
The AE used a single power supply as the bias amplifier of ADS1299 AFE provides a fixed DC potential of 2.5 V (AVDD/2). This potential drives the subject’s input common mode
It has built a vibrant small and medium capitalization market, the strongest derivatives market in Central and Eastern Europe, a fixed income trading platform, In 2010, Warsaw
attending interviews. Findings show that the majority of youth connected continued success in navigating the labour market to approaches and ingredients, which fall outside of pure
Data, computing, metadata, workflow management Science gateways for productivity. Important goals – Federated security – Big Data – Resilience – Usability
Another factor powering M&A activity is China, which is pursuing the development of its semiconductor industry through acquisitions; its government has announced plans to spend