Simultaneous heat and mass transfer from a vertical isothermal surface

University of Windsor University of Windsor

Scholarship at UWindsor

Scholarship at UWindsor

Electronic Theses and Dissertations Theses, Dissertations, and Major Papers

1-1-1979

Simultaneous heat and mass transfer from a vertical isothermal

Simultaneous heat and mass transfer from a vertical isothermal

surface

surface

A. B. M. Abdul Hye University of Windsor

Follow this and additional works at: https://scholar.uwindsor.ca/etd

Recommended Citation Recommended Citation

Hye, A. B. M. Abdul, "Simultaneous heat and mass transfer from a vertical isothermal surface" (1979). Electronic Theses and Dissertations. 7335.

https://scholar.uwindsor.ca/etd/7335

This online database contains the full-text of PhD dissertations and Masters’ theses of University of Windsor students from 1954 forward. These documents are made available for personal study and research purposes only, in accordance with the Canadian Copyright Act and the Creative Commons license—CC BY-NC-ND (Attribution, Non-Commercial, No Derivative Works). Under this license, works must always be attributed to the copyright holder (original author), cannot be used for any commercial purposes, and may not be altered. Any other use would require the permission of the copyright holder. Students may inquire about withdrawing their dissertation and/or thesis from this database. For additional inquiries, please contact the repository administrator via email

2. HYE, A.B.M. ABDUL.

Simulta~eous

heat and mass ... surface. Phd. 1979.

SIMULTANEOUS HEAT AND MASS TRANSFER FROM A VERTICAL ISOTHERMAL SURFACE

by

A. B. M. Abdul Hye

A Dissertation

submitted to the Faculty of Graduate Studies through the Department of Mechanical Engineering in partial fulfillment of the requirements for the

Degree of Doctor of Philosophy at the University of Windsor

2. HYf

National Library of Canada

Bib I i oth~que national e du Canada

CANADIAN THESES ON MICROFICHE

0

THlSES CANAD/ENNES SUR MICROFICHE

"LE OF THESIS/n~£0£LA ~~:~~~~~~S~i=m=~~t~a=n~e~o~u=s~h=e=a~t~a=n~d~m=a=s~s~t~r~a=n~s~f~e~r~~fr~o=m~=a~~~~~~~~~

vertical isothermal surface.

IVERSITY IUNIVERSITE University of Windsor, Windsor, Ontario

3REE FOR WHICH THESIS WAS ~ESENTED/

~AOEPD~LEOUUCEITETHEUWTM~fflTh~~~~~~~-P-h_._D _.~~~~~~~~~~~~~~~~~~~-IR THIS DEGREE CONFERRED/ANNE£ O'OBTENTIDN DEC£ GRAOE _ _ ~M:.:;a""y--=1.,.9._.7""'9..._ _ _ _ _ ~-~~--~----~--ME~SU~~ISOOmOMOUO/MCIT~Mmiu_~---~D~r~·~T~·~W~·~M~c=D~o=n~a=l~d

~---~--~--~---mission is hereby granted to the NATIONAL LIBRARY OF L'autorisation est. par Ia pr~sente, accord~e ~ Ia BIBLIOTHE-NADA to microfilm this thesis and to lend or sell copies QUE NATIONALE DU CANADA de microfilmer cette tMse et the film. de preter ou de vendre des exemplaires du film.

1 _{author reserves other publication rights, and neither the} L'auteur se reserve les autres droits de publication; ni Ia sis nor extensive extracts from it may be printed or other- tMse ni de longs extraits de celle-ci ne doivent etre imprimes e reproduced without the author's written permission. ou autrement reproduits sans f'autorisation ~crite de !'auteur.

"EDIDATE

~

n

ABSTRACT

An analysis of simultaneous

diffusion

and

heat

transfer

from a

vertical isothermal flat plate

has been

carried

out.

The analysis

considered only the natural convection flow around

the plate with

uniform velocity of injection of the injected

gas

along

the plate

into

the surrounding air. The temperature of the

plate was

always

higher

than

the ambient temperature.

The analysis was carried out to determine the effect of diffusion

on heat transfer and conversely, the effect of heat transfer on diffusion.

That is,

to

investigate the diffusion thermo effect (DT) or

Dufour

effect

(the

heat flow due to concentration

gradient)

and the thermal

diffusion

effect (TD) or Soret effect (the diffusive flon of

mass

due

to temperature gradient). The property variations due to te

mp

erature

and concentration

were

also considered.

In order to obtain the

analytical

solution, the

governing

equations

(two-dimensional, steady state)

were transformed

by a

p9ly

ing standard

similarity transformations. Standard

perturbation

techni

qu

es

were used

to

obtain infinite sets of ordinary differential equations in order of

increasing

powers

of the expansion

parameter

('blowing

parameter').

The

first three sets of equations

were

solved by Rosenbrock's

optimization

method

of

hill-climbing

for selected

gases as

the

diffusing mediums

and

selected

surface

tem9eratures.

The selected

gases were helium,

air

and

carbon dioxide

and the wall

temperatures

were 310, 330, 350, 370K.

It

was

found that

the

series expansion

was

conver

g

ent

only

for lo

w

injection velocities.

these

low injection velocit

y

ran

ges

,

the

thermal diffusion effect was about

2%

of

the

heat transfer rate at the

wal

l.

M

ost

of the heat was transferred

from

the

wa

ll

by

con

duction

and

by

the

effect of diffusion thermo. The effect

of

pro?erty variations on

the heat

transfer

rate due to tem9erature and

concent

ration

vas about

5%.

Consequently,

the thermal diffusion effect

neglecte

d

and the

property variations

retained

only

in

the bu

o

yancy force

T

h

is

~ade

the

equations considerably less comulicated

and decreased

required computer time. With these simplifications,

the

first five sets

of equations

were

solved.

'!l

i thin the limit

of

the conver

g

ency

of the

series,

the maximum possible

numerical values

of

the injection velocity

at the

wall were

0

.00375

cm/s for helium,

0.0375

cm/s for air and

0

.075

cm/s

for carbon dioxide

w

ith

the ratio of wall temperature to the

ambient temperature

of

1.1.

The experiment was

done with

an interferometer

employed two

lasers

of different

wave

lengths. A sintered stainless steel

porous

plate

was

used as the wall. A heated

gas

(helium, air

o

r

carbon dioxide)

was injected from behind the plate. The velocity of injection

was

uniform over the surface of the plate. Under steady state condition,

the

temperatures of the wall and the gas were the same and uniform. From the

interferograms, the temperature and the concentration

distributions

in

the

boundary layer were obtained and

compared

with

the analytical

results.

It was found that

the local

values

of concentration

were within

5%

of the analytical values at different points in

the

boundary layer

except at the wall where

t

he concentration

differed by

30%.

This large

deviation was due to the graphical

extrapolation

method use' to locate

the

correct

position

of the

w

all in

the

interferograms.

The experimental

values of temperature were

w

ithin

5%

of the analytical values. As

air

injection did not involve any

concentration,

the si

3

ultaneous equations

used to calculate temperature

were

simplified. The experimental results

for air injection were

·:.ri

thin

5

%

of the analytical results.

ACKNO'NLEDGEMENT S

The author is

g

rateful to Dr. T.

N.

M

cDonald,

H

ea

d

of t

h

e

Department of Mechanical Engineerin

g

, for

h

is con

t

inuous su

pp

ort

and interest.

The author wishes to express his deep

g

rati

t

u

d

e and sincere

thanks to Dr.

W

.T. Kierkus for his invaluable

g

uidance, help and

encouragement during the course of this study. In particular, t

h

e

author would like to express gratitude for the ent

h

usiastic counsel

given by Professor W.G. Colborne, Dr. C.C. St. Pierre and Dr. J.E.S.

Venart.

Thanks are also due to Messrs. Robert Gasper,

N

azrul Islam,

Thomas Moore, A.K. Sethi for their help and co-operation and to

c.

Cada and Robert Tattersall for their technical assistance in

fabricating the apparatus.

To his wife, the author wish simply to say that there are no

words

w

hich can adequately express his feelin

g

s for the support

she has given to enable him to reach this point.

Acknowledgement is made to the National Re

s

earch Council of

Canada for providing financial support.

T

AB

LE OF CO

N

TE

NT

S

ABSTRACT

ACK

NO'.'/

LEDGE

H

E

N

T

TA

B

LE OF CO

N

TE

N

TS

LIST OF FIGURES

LIST OF TA

B

LES

LIST OF SYMBOLS

CHAPTER

I

I

N

TRODUCTIO

N

II

LITERATURE

S

URVEY

2.1 General

2.2 Free Convection

2.3 Heat and

Ma

ss Transfer

A.

Evaporation

B. Suction

& Injection

III THEORY

IV

v

VI

3.1

Thermal Diffusion and

Diffusion Thermo

3.2 The Governing Equations and

Boundary Conditions.

3.3

Transport Properties

METHOD OF SOLUTION

EXPERI

M

E

N

TAL A

R

RA

N

GEMENT

5.1 Major Components

5.2 Temperature

M

easure

m

ent

5.

3

Concentration

M

easure

m

ent

5

.

4

Instrumentation

EX PE

RI >

AL

P

J

O

C

ZDUR

E

vi

...

P

age

iii

v

i

vi

i

i

xi

xi i

VII

METHOD OF

CALCULATION

&

INTERPRETATIO

N

VIII

RESULTS

IX

8

.1

Effects of

D

iffusion

The

rmo

and

Thermal

Diffusion

8.2

Effects of

Different

Property

Ratios

8.3

Extension of Solution

with

Some Simplifications

8.4

Experimental Results and

Comparison

CO

N

CLUSIONS

TCES

APPE

IDICES

vii

47

47

52

52

63

81

83

LIST

OF F

I

GU:q:ss

P

a

g

e

l

.l

M

o

d

el Studie

d

3

3

.1

C

o

-or

d

inate Syste

m

5.1

G

eneral Arrange

m

ent of E

x

peri

m

ental

App

ara

t

us.

33

5

.2

G

eneral vie

w

of t

h

e experimental set-

u:9

.

34

5.3

D

etails of the porous plate, baffles, t

h

er

m

ocou

p

les.

35

5.4

Optical layout

.

of interfero

m

eter.

37

5

.5

The ca

m

era facing the interferometer.

38

5.6

Test section of the interf

e

rometer.

39

7.1

Determination of fringe shifts.

44

7.2

Interpolation of fringe shifts to same y position.

4

5

8.1

Analytical heat Transfer re.sults for Heli

·

um Injection

48

8.2

8

.3

8

.4

8

.5

8

.6

8

.7

8.8

8

.9

8.10 8.11

8

.12

8

.1

3

Anal

y

tical Heat

results for

co

2

injection

Analytical Heat Transfer results for Air injectio

n

.

Effect of terms on perturbation series solution.

Velocity distribution for helium injection.

Velocity distribution for

co

injection.

Velocity distribution for air injection.

Temperature distribution for helium injection.

Temperature distribution for

co

2

injection.

Temperature distribution for air injection.

Concentration distribution for helium injection.

Concentration distribution for

co

injection.

Temperature distribution for helium injection

w

ith

v

=

m/s.

w

vi

i

i

8

.1

4

8

.15

8

.16

8

.17

8

.1

8

8.19

8

.20

8.21

8.22

8

.23

8

.2

4

8.25

8

.26

8.27

9.1

9.2

9.3

9

•

.5

9

.6

15.1

Concentration distribution for

helium

injection

with

=

0

.

00002

m/s.

w

Temperature distribution for helium

injection

with

= 0

.

0000275

m

/s.

w

Concentration

distribution for helium

injection

with

v

=

0.0000275

m/s.

w

Temperature

distribution for helium

injection

with

v

::.0.

0000311

m/s.

w

Concentration distribution

for helium

injection

with

v

=

0.0000311

m/s.

Temperature distribution for

co

2

injection with v

=

0.000378

m/s.

w

Concentration distribution for

c

o

2

injection with v

=

0.00037

8

m/s.

w

Temperature distribution for

co

2

injection with v

=

0.000507

m/s.

w

Concentration distribution for

co

2

injection with vw=

0.000507

m/s.

Temperature distribution for

co

2

injection with vw=

0.000624

m/s.

Concentration distribution for

co

₂

injection with vw-=-

0.000624

m/s.

Temperature distribution for air

injection with v

=

0.000201

m/s.

w

Temperature distribution for air

injection with vw::

0.000273

m/s.

Temperature distribution for air

injection with vw=

0.000316

m/s.

Correlation chart for flowmeters.

Calibration chart for flowmeter - 1.

Calibration chart for

- 2.

Calibration

chart

for flowmeter

-

3.

Calibration chart for flowmeter -

4.

Calibration chart

for flowmeter

-

5.

Red

fringe with

no

heat and mass transfer.

15.2 15.3

15.4

15.5

15.6 15.7 15.8 15.10 15.11 15.12 15.13 15.14 15.15 15.16 15.17

15.18

15.19

15.20

Green

f

ri

ng

e

w

it

h

no

h

ea

t

and

m

ass

t

r

a

ns

f

er.

Red frin

g

e for

h

elium

i

n

j

ec

t

i

o

n

w

i

th

=

m

/ s.

w

Green frin

g

e for

h

elium injection

w

i

t

h

=

m/ s •

Red frin

g

e for heliu

m

in

j

ection

w

ith

v

= 0

m/s.

Green fringe for helium injecti

o

n

w

it

h

Vw= 0.0000275

m/s.

Red fringe for helium injection with

vw

=

m/s.

Green fringe for helium injection w

i

th

vw

=

m/s.

Red frin

g

e for air injection with

m/s.

w

Green fringe for air injection with

vw

=-

m/ s.

Red frin

g

e for air injection with

v

= 0.000273

m/s.

Green fringe for air injection with

v

=

m/s.

w

Red fringe for air injection with

v

m/s.

w

Green fringe for air injection with

v

=

m/s.

w

Red frin

g

e for

co

2

injection with

v

=

m/s.

w

Green fringe for

co

2

injection

w

ith

v

=

m/s.

w

Red frin

g

e for

co

2

injection

w

ith

w

Green fringe for

co

injection with

v

=

m/s.

Red fringe for CO? injection

w

ith

=-

m/s.

w

Green frin

g

e for

co

2

injection

w

ith

v :::

m/s.

w

X

160

161

162

163

164 165 166 167 168 169 170

171

1.1

6

.1

8

.1

8

.2

9

.1

9

.2

9-3

9

.4

9

-5

11.1

11.2

11.

3

11.

4

12.1

12.2

12.

3

LIST OF

T

A

B

L

E

S

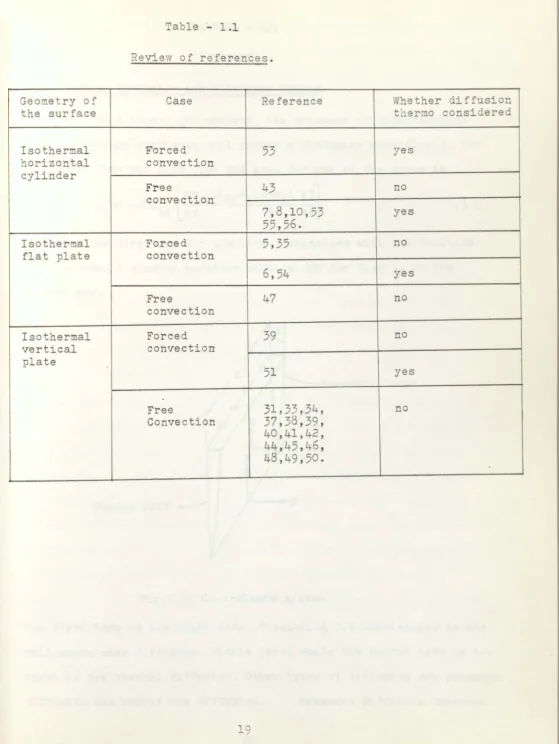
Revi

ew

of ref

e

rences.

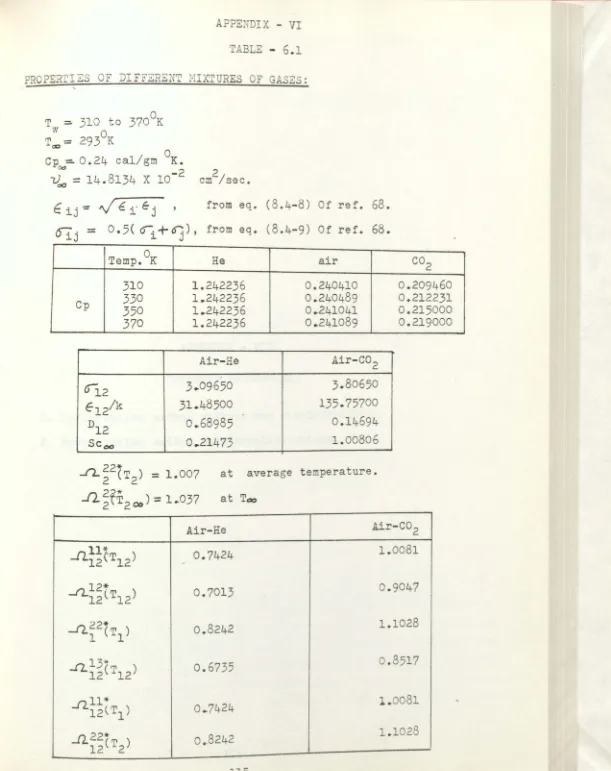
Pro

perties of di

fferent

gases.

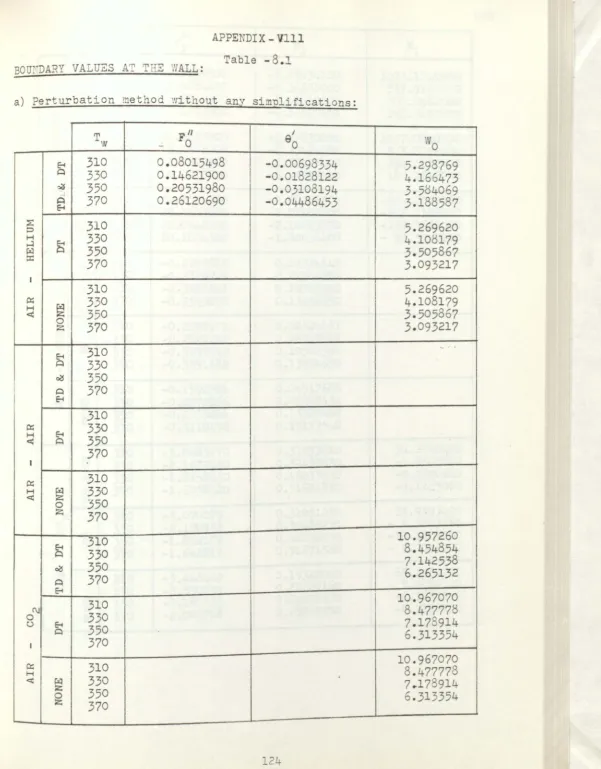
Boundary values at t

he

nall b

y perturbat

i

on

method

w

ithout any sim

plific

at

i

on.

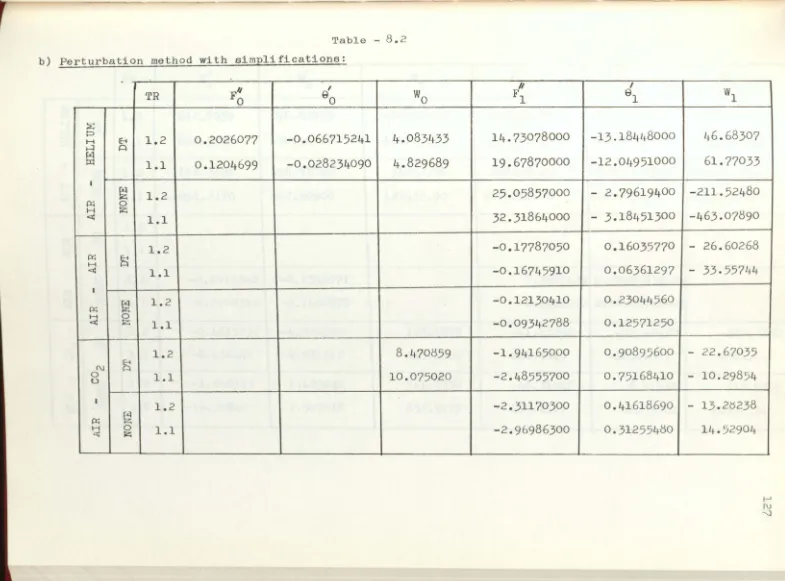
Boundary values at the

w

al

l

b

y per

tur

bation

met

h

od

w

ith si

m

plification.

Calibration for flowmeter-1 f

or dif

f

erent

gases.

Calibration fqr flowmeter-2 for different

gases.

Calibration for flowmeter-3 for different

gases.

Calibration for flowmeter-4 for different gase

s

.

Calibration for flowmeter-5 for different

gases.

Experimental data.

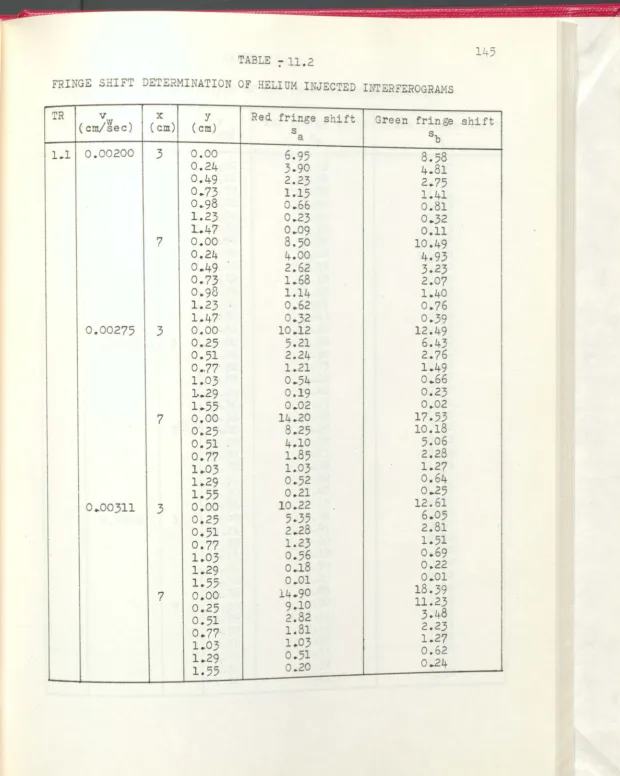
Fringe shift determination of helium injected

interferograms.

Fringe shift determination of air injected

interferograms.

Fringe shift determ

ination of

co

_{2 injected}

-

interfero

grams ..

Index of refraction of different gases.

Index of refraction of different gases at

different temperatures.

Physical constants of different

gases.

xi

Pa

g

e

1

9

11

5

l2W.

127

1

3

6

1

37

138

13

9

1

40

1

4

3

1

45

146

1

4

7

1

4

8

1

49

Symbol

A

Al, A2'

*

Al2' AD B2' B3' c2' c3'

*

"

I I I f F. 1. g Gr GrAB h ji k

LIST OF SP1BOLS

Quantity

A

3, .••• Different Property Constants Property Constants

Different Property Constants Different Property Constants Property Constant

Specific Heat of Mixture at Constant Pressure Specific Heat of Component i at Constant Pressure Coefficient of Binary Diffusion

Nlj-N2j

Abbreviation for Diffusion Thermo.

M

2

/M

1

-l

H2/Ml

(~pl/Cp2)-l

2 Function, F ₀(">() -t- F l ("1) ~ -t- F 2(~)

5

I I I 2

Fa+ Fl~

+

+ ...

.

" " " 2

Fo+Fl_s

+

+ ...

.

-t-

S

+

+

Exterior Force Exerted on a Unit Mass of Component i

Acceleration due to Gravity Heat Transfer Grashof Number Mass Transfer Grashof Number Specific Enthalpy of Mixture

Diffusive mass Flux of Component i

Ther~al Conductivity of Mixture

xii

Units

m

-

3/h

Dimensionless Dimensionless Dimensionless Dimensionless Dimensionless

J/(kg.K)

J/(kg

.

K)

2

m

/s.

m3/mol.

2

J/(s.m .K) Dimensionless Dimensionless Dimensionless Dimensionless Dimensionless Dimensionless Dimensionless 2 m/s .

2

m/s •

Dimensionless Dimensionless

J/kg

.

2

kg/(m

.s)

Symbol k. l

kT

K.

H

.

R

s

.

TR

*

Thermal Conductivity of Component i

Thermal Diffusion Ratio, ~.x

₁

₂

Mass of Component i Created by Chemical Reaction per Unit Volume and Unit Time.

Width of the Porous Plate

Lewis Number, k/(P.Cp.D

12>

Molecular ~eight of the Mixture

Molecular Weight of Component i

Index of Refraction of Component i

Molar Refractivity of Component i

Nusselt Number

Total Pressure

Prandtl Number, ~.Cp/k

Heat Flux per unit Time and Area

Gas Constant of the Mixture

Universal Gas Constant

Fringe Shift of Beam j at any point

Property Constants

Schmidt Number, "l>/D₁₂

Sherwood Number

Time

Tem~erature

Abbreviation for Thermal Diffusion

Absolute Temperature _- Ratio, T _VI /T~ _...,

Reduced Temperature, kT/ E

Com~onent of Velocity Along x-Direction

Different Property Constants

Component of Velocity Along y-Direction

Hass Fraction,

Pi

/

f

w

(•1.)

3

+

3

+. · ·

xi i i

Units

W/(m.K)

Di::nensionless

3 kg/m .s.

m Dimensionless kg/mol. kg/mol. Dimensionless Dimensionless 2 N/m .

Dimensionless

J/(m2

.s)

J/(kg.K)

J/(mol.i\) Dimensionless Dimensionless Dimensionless Dimensionless s K 2 kg/(m

.s)

Symbol

'

~

,xk

y

y~ _'yk

~

o(l2 f i

"1__,

lf

~p

~

k

A

p

fi

e

'

e

"

e

"I' >.e .,, ' 'i? 2

·

"

o

.:;,+

+

" " 2

w

5 +

+

Distance Along the Surface from the Leading Edge

Mole Fraction of Component i

Pro~erty Constants

Distance Normal to the Surface

Property Constants

Property Constants

Thermal Diffusion Factor(s~ecies l into species 2)

Lennard-Jones Potential Parameter of Component i

Similarity Parameter,

Ax-l/

4

~yyf.

Viscous Dissipation Function

Stream Function

.

P;

P

Blowing Parameter,

vwx

!(4AlJ

~

)

Boltzmann C~nstant

Wave Length of Light j

Absolute Viscosity of Mixture

Absolute Viscosity of Component i

Kinematic Viscosity

Density of Mixture=

f\

+

f

Local Density of Component i

Molecular Collision Diameter

x:iv Units Dimensionless Dimensionless m Dimensionless Dimensionless m Dimensionless Dimensionless Dimensionless J Dimensionless J/(kg.m3 ) 2

m

/s.

Dimensionless Dimensionless J/K

it

m2/s

kg/m3

kg/m

3

Dimensionless

Dimensionless

XV

Symbol Quantity Units

__f2_ l l * ( T*

JL

*

12 1 ), 12 (Tl2), 12 (T2)' Different Omega Integrals

to Calculate Molecular Force Constants Dimensionless

Subscript

l Injected Gas 2 Ambient Gas

i ==1,2

0 No Blowing

w

oo Condition at y -oo

m Mixture

a Red Beam from He-Ne Laser b Green Beam from Ar-Ion Laser

j

=a,

k,n Summation Indices

Superscript

First Differentiation with Res~ect to

_Yl

II _{Double Differentiation} with Res:)ect to

' t

I I I _{Triple Differentiation} with Respect to ~

2.

an

CHAPTER-I

INTRODUCTION

Diffusion is said to occur in a mixture when there is a relative motion of its components. Such relative motion commonly arises

because of inhomogeneity of composition. In a binary mixture in

which the composition is not uniform the components move in opposite directions, each down its concentration gradient, with the result that,

if the temperature is uniform, the inequalities of composition are

reduced and ultimately removed. Diffusion originating in this way is 'ordinary' or 'concentration' diffusion. This is governed by the

Fick's law of diffusion. Diffusion may, however, have other causes;

in parti~ular, i t may be due to non-uniformity of temperature within a mixture. Diffusion from this cause is called thermal diffusion or Soret effect.

Thermal diffusion consists in a relative motion of the components of a mixture arising from temperature differences within the mixture.

It leads, therefore, in a mixture initially of uniform composition,

to the development of a concentration gradient. Since this concentration ~radient in turn causes ordinary diffusion tending to eli~inate the

gradient, a steady state is possible in Nhich the separating effect of thermal diffusion is balanced by the re~ixing effect of ordinary diffusion. ·~hether or not such a steady state exists, i t is cenerally true that when the temperature of a mixture is not uniform its

2

difference in composition of the mixture in the t~o bul~s is establis~ed.

3ecause the ~olecules of the light gas have more kinetic ener~y and so

they wi l l occupy more s~ace in the up_er bulb. Thermal li~fusion thus

brings about a )artial seuaration of the com~onents of the initially

unif~rn Tixture.

In

1873

gases throu~h porous partitions and the accompanying temperature

changes'. In the experiments t here described, a ~orous vessel, in

which a sensitive thermometer was inserted, was contained within

another vessel. The interior of the porous vessel was in communication

through a glass tube with the atmosphere so that the pressure ~ithin

i t was constant. When this inner vessel vas filled with air, and

hydrogen was circulated in the space between the two vessels, Dufour

observed that as the hydrogen diffused into the inner vessel the

thermometer indicated a fall in temperature. He found a similar effect

when the porous vessel was initially filled with carbon dioxide and

air was circulated about it. Dufour expressed the view that the

temperature changes occur, not throughout the gas but near the surface

of the porous partition. In this way he discovered what has since

come to be called the diffusion thermo effect. or Dufour effect.

The diffusion thermo effect consists in a transport of heat as

part of the process of diffusion in a gas mixture; i t is therefore

associated with the existance of a concentration gradient. The effect

is initially connected with thermal diffusion, the molecular transport

associated with a temperature gradient. Thus thermal diffusion and

diffusion thermo are thermodynamically coupled phenomena. so i f t;·/o

gases initially at the same temperature interdiffuse there is a

transport of heat, with a consequent develo,rnent of a tem~erature

2

difference in composition of the ~ixture in the t~o bul~s is establis~ed.

9ecause the ~olecules of the light gas have more ~inetic ener~y and so they will occupy more S?ace in the upper bulb. Thermal li:fusion thus

brings about a ,ar tial senaration of the co~~onents of the initially unif~rn ~ixture.

• _In

₁₈₇₃

gases throuGh porous partitions and the accompanying temperature

changes'. In the experiments there described, a ,orous vessel , in

which a sensitive thermometer was inserted, was contained wi thin

another vessel. The interior of the porous vessel was i~ communication

through a glass tube with the atmosphere so that the pressure ~ithin

i t was constant. When this inner vessel was filled with air, and

hydrogen nas circulated in the space between the two vessels, Dufour

observed that as the hydrogen diffused into the inner vessel the

thermometer indicated a fall in tem~erature. He found a similar effect

when the porous vessel was initially filled with carbon dioxide and

air was circulated about it. Dufour expressed the view that the

temperature changes occur, not throughout the gas but near the surface

of the porous partition. In this way he discovered what has since

come to be called the diffusion thermo effect. or Dufour effect.

The diffusion thermo effect consists in a transport of heat as

part of the process of diffusion in a gas mixture; i t is therefore

associated with the existance of a concentration gradient. The effect

is initially connected with thermal diffusion, the molecular transport

associated with a temperature gradient. Thus ther~al diffusion and

diffusion thermo are thermodynamically coupled phenomena. So i f bto

gases initially at the same temperature interdiffuse there is a

transport of heat, with a consequent develo,rnent of a temperature

In the gas ~ixture, heat is transferred by conduction, co~vection

and diffusion ther~o effect. The effect of radiation is negl igi ble.

If the gas is at a particular temperature, t~e internal energy (heat

content) of the two species are dif~erent and during the ~recess of

diffusion, the two s~ecies will exchange energy. This is called the

heat transfer by interdiffusional convection.

This process of si~ultaneous heat and ~ass trans~er has received

considerable attention over a number of years as i t is closely related

to problems of drying, surface evaporation or condensation, suction or

injection cooling etc. In general, the temperature of the surface can

be higher or lower than that of the surrounding fluid and the direction

of the diffusive flow can be from or toward the surface. The present

study was concerned only with the case when the surface temperature

is higher than the ambient fluid and with the injection of different

gases (helium, air, carbon dioxide) into the boundary layer. The

velocity of the injected gas was uniform over the plate surface. The

process studied was natural convection, two-dimensional, steady state.

Under steady state condition, the temperature of the injected gas and

the wall ~ill be same. The a~bient temperature is considered constant.

The geo~etry of the model studied is shown in Fig. l.l.

Vertical Porous

Wall of Infinite Extent.

Tw _ constant

v

=

'Injected Gas'

X

y

Fig.l .l: Model Studied.

'Ambient Gas'

T₀₀

=

T.;, ). T00

4

Basic

studies

cl

o

sel

y

relate

d

to

nresent

were don

e

by Gross

et

al

1

*

Sziklas

2

,

Go

llnic

k3

and Scott4

~he

re

t~e

effect

on

heat transfer

ra

te

for

various foreign

s

ases

injecte

d

into

the b

oun

dary

layer

th

r

ou

per~eable

surf

a

ce

were

Results

of

a

later analysis

done by

Baron

5

siowed

that when

a

con

siderably lighter

gas

(heliu~,

hydrogen)

trans

p

ired into

a

heavier one

(air),

the ratio of

heat transfer

fro

m

the surface

decreased

ra'!_Jidly. The

d

ifference

between the

rate

of

h

eat

transfer for

a

single component

g

as

,

and

component

ga

ses (transpiring

gas and

surrounding fluid) increased when the molecul

a

r

weight difference

of the tvro

gases

(transpiring gas and ambient fluid) increased. Recent

6

7

.

8 9

10 11

studies by Sparrow et

al

' ,

Tewflk et al

'

'

'

have

indicate

d

that the effects of thermal diffusion and diffusion ther

m

o

contribute

to the difference.

In the

present

analysis the relative effects of TD and DT on

heat

.

transfer were

analysed

for different blowing

The variation

of

properties

du

e to temperature and concentration

also

considered.

From the analysis, the temperature

and

concentration

distributions at

different points in the boundary layer

were

calculated.

Experimental

results

obtained

by using a

H

ach-Zehnder

interferometer

were

co

mpared

with the analytical

results.

CHAPI'ER - II

LITERATURE SURVEY

2.1. GENERAL:

12

Nusselt was one of the first authors to investigate

convective mass transfer in relation to an engineering application.

12 13

He ' remarked that under certain circumstances the differential

equations and boundary conditions for heat and mass transfer

respec-tively were mathematically equivalent, so that these processes were

similar. If this similarity holds, then the equations governing mass

transfer may be derived from the equations governing heat transfer

and vice versa. Schmidt1

4

heat and mass transfer for free convection. Nusselt and Schmidt both

developed their similarity relations under the assumption that the

mass flux of a component caused by ordinary diffusion was proportional

to the negative gradient of the mass concentration of the component

considered. This means that they assumed that the diffusive potential

was given by the mass concentration. This assumption had already been

introduced many years earlier by Fick15 and is sometimes called

Fick's diffusion law. Ackermann16 triel to show that for simultaneous

heat and mass transfer i t was better to use the partial pressure as a

diffusive potential. 'rhis point of view has been accepted by Eckert17,

18

19

.

20 21 22

Jakob and Sherwood et al • Later on Spa2..dlng ' ' proposed that

simultaneous heat and mass transfer might be described in a very

convenient way if the fractional mass concentration was used as the

diffusive potential. Merk2

3,

formulated the basic equations in a general vectorial form which

could be used to analyse any specific problem of simultaneous heat

and mass transfer.

6

Nusselt in his works concluded that the process of heat and mass

transfer were similar in nature because the energy equation and the

diffusion equations were si~ilar in form except that the energy

equation had the Prandtl number, Pr, while the diffusion equation

had the Schmidt number, Sc. Thus the two processes can be analogous

•

only i f the Prandtl number and the Schmidt number ~ere equal in

magnitude, (i.e., the Lewis number, Le, which is the ratio of Pr to

Sc, is equal to unity). If mass transfer occurs, mass is absorbed or

given up by the surface of the ~ass-exchanging body. As a result a

finite velocity perpendicular to the surface exists, which is missing

in pure heat transfer. Nusselt later drew attention to the existence

of this velocity, which is sometimes called the velocity of

Stefan-Nusselt or the convective compensating velocity. The occurance of

this convective compensating velocity in mass transfer process disturbs

the above analogy between mass transfer and pure heat transfer. On the

assumption that Le is unity, i t is easy to relate the heat transfer

to the mass transfer if both process occur simultaneously. ~he

influence of convective velocity on the mass transfer has been

calculated by Schuh2

5;

and Emmons28 , within the range of 0. 6 L :::5c L 2. Merk24 extended

this range using a perturbation method to 0.5L Sc ~oo.

2. 2. FRE:S

co

Eckert 2

9

heat transfer. Ustrach considered an isothermal vertical plate with

free convection flow. The body force created by the difference in

density was the driving force for the flow. The flow was found to

be de pendent on the Grasho f number alone. For large Grasho f nuutber,

7

Prandtl's forced flow boundary layer theory. Velocity and temnerature

distributions for

Prandtl

numbers of

0

.72,

0

.733,

1, 2, 10, 100,

1000

w

ere

He

did not consider the effect of variable

~roperties

due to temperature.

Hi

s

works showed the influence

of

Prandtl

on free

heat transfer. For the same

temperature difference between the wall and the surrounding, the

heat

transfer rate increases

with

increasing Prandtl number.

2.3.

&

A •. CONDENSATIO!'T & EVAPORATION:

Somers3l used evaporation and condensation

processes for the

study of heat and mass transfer in a free convection boundary layer

on a

wetted

isothermal vertical flat plate.

This

problem

presents

itself in the practical case of vaporization cooling

of

equipment

without

forced circulation of the ambient gas. Somers used

an

integral

method

for this

problem

taking into account the non-zero

wall

velocity

arising from the mass transfer.

His

work

was

concerned

with the

combined thermal and diffusive flow that

would

arise adjacent

to

the

vertical plate in a non-saturated atmosphere. The condition of very

small diffusing species concentration

was

used and an analysis

was

carried out for uniform surface temperature and

diffusing

species

concentration. Somers came up

with

a relation between

the

ratio of

heau

transfer and mass transfer as a function ofvfL,e. Somers

did not

consider

the effect of variable

properties

and

the behaviour

of

therT.al diffusion

and

diffusion

on

heat

and

mass

transfer.

N

aka

mu

ra3

2

studied

the

si~ultaneous

transf8r of sensible and

latent heat

wh

en

the

materi

al transferred

was water vapor, as the case

in many

where free convection

rnight

be important.

8

of enthalphy differences. ~ru~amura also neglected buoyancy forcss

due to concentration distributions.

~ath

ers

for~ulated

mass transfer i n ter~s of the boundary layer differential equations

resulting fro~ force-momentu~, energy and chemical species conservation,

at very low concentration. Neglecting inertia effects, the resulting

equations were solved by analog computer for Pr=l.O and Sc=0.5-l0

for the ratio of species and thermal diffusion buoyancy effects of 1.0

and 0.5. Resulting trans~ort information appears to support the ~

factor of Somers31• His

ex~erimental

na~thalene

benzene diffusing from a sphere in air were found to be 20% a~ay from

the numerical results. The reason for this discre~ancy may be due to his assumution of constant physical ~roperties and exclusion of the

effects of thermal diffusion and diffusion thermo •

.

~!

ilco~4

assumptions of uniform conditions along a surface, arbitrary profiles

of velocity, te~perature and concentration. ~e d8duced the trans~ort

equations vrhich showed the factor

,y"Le.

the exact results for flows driven entirely by thermal diffusion.

Differencss were ap~reciable and the comparison did not validate the

use of a simple integral method analysis for convection with the

combined effects of convective heat and mass transfer. Also, his

analysis did not include the effects of thermal diffusion and

diffusion thermo.

Li0htfoot3

6

asy:?:~totic

>)

Gr

>>

transfer Grashof nu~ber) in which the ~ass transfer boundary layer

9

substantially

all

convection resulted from

inequalities.

Hi

s

relation for

Nusse

l

t

number

was not

in

good agreement

·:1i

th the

geYJ.e

r

al

result of

'.

'/

ilco

x34

,

'

.vhere

the

limiting

case

.vas

P

r - s c .

Adams and

i'1

cFadden37 reported

experimental

me

asure

m

e

n

ts of

th

e

h

eat

and

m

ass

transfer parameters using a

Ma

c

h

Zehnder

interferometer

during

the su

bl

i

m

ation of

P-dichlorobenzene (Sc

=

2.23)

from

a

heated

vertical surf

a

ce into air. T

h

e

body

force created

by

this heavy organic vapor in the boundary layer opposed the

upward

thermal body force caused by heating the surface. Presentation of

the data in terms of the effective net buoyant force predicted by

Somers3l resulted in experimental data being 10 - 15% lower than

any of the integral method results.

DenBouter et al3

8

reported

an

experimental study of

simultaneous

heat

and mass transfer

by an

electroche

m

ical

me

thod.

A

vertical cop

p

er

,

late

w

as

maintained

at a constant temper

atu

re

in a copper sulphate-sulphuric acid solution.

Measurements

we

re

made w

ith the two cases

wh

en the buoyancy effects

\':e

re aidin

g

and

wh

en op

p

osing.

The

heat and

mass

transfer

correl

a

ted

in

terms

of a combined buoyancy effect

agreed

w

ell for

the

effects

of

aiding.

H

owever, for the effects

opposed, the

in

the

magnitude

of combined

heat

and mass

transfer

rate

was

m

ore

than

30%. Perhaps even

that level

of

a

g

ree

m

ent

was surprising

since

Pr

10 and

Sc

::::=

2

000

apply in

t

h

eir stu

dy

.

Manganaro and

Hanna39 d

iscussed

the equations

wh

ic

h

~ould

g

overn si

multan

eous

thermal and

che

mi

cal

S?ecies transport in

a

10

functions of both temperature and composition.

Both forced

and free

convection flows were considered.

fhey

considered large mass transfer

rates

from

the surface in order to rnini::nize

the

effect of chemical

reactions. Practicc:Ily t!r:ts

made-

the

s-olU:

_

t±on.,_,

-

fi

cult

to

achieve.

The consideration of different properties as arbitrary functions of

temperature showed that property variations were generally more

important for free convection than for forced convection.

Saville and Churchill 40 considered simultaneous

thermal

and

species diffusion caused by buoyancy forces for very low concentration

levels. They used the formulation of Saville and Churchill4l

tor

natural convection adjacent to general

surfaces like horizontal

cylinders and vertical axisymmetric bodies. Attention was restricted

to asymptotic processes in terms of the Prandtl and Schmidt numbers.

The dependence of the transport parameters was

found for Pr =Sc - o ,

for

Pr= sc-

=,

for Pr--o and sc.-oo, and for Pr and sc--oowi th

Sc )) Pr. For Pr= Sc, the processes were a 3ymptotic. But the t'.'IO

processes would be asymptatic onl-y if the effects of

diffusion and diffusion thermo were

So the calculation

of transport parameters only on the basis

of

the values of

Pr

and

Sc

·

camrot' be justified.

Bottemanne

·

42 made a very simple theoretical

in~estigation

of the simultaneous heat and

transfer f0r a vertical isothermal

surface

r

:fith Pr=O.?l and Sc =0.63. He assumed constant properties and

neglected the effects of thermal diffusion

and

diffusion thermo.

His

experimental work 43 with a vertical isothermal cylinder with

s

h

o

w

ed

g

ood agree

m

ent

w

ith his

th

eore

tic

al resu

l

ts

4

2

of

is

oth

er

m

al

v

ertical surface.

H

ere

P

r

w

as ver

y

c

lo

se

to S

c.

fo

r so

m

e

oth

er

substance having Sc much differen

t

t

h

an

P

r

, th

e

d

i

ffer

e

nc

e

b

e

t

;

v

een

th

e

and t

h

eoretical resu

lt w

ou

ld

increase even if the

effect of thermal diffusion and dif

f

usi

o

n

th

ermo

w

ere

n

o

t

c

o

nsi

d

ere

d

as s

h

own by Lig

h

tfoot3

6.

B. SUCTIO

N

&

I

N

JECTTON:

Smi th35 developed a theory which

. described the e f feet of

diffusion on the dynamic and thermal characteristics of a laminar

boundary layer on a flat plate in steady compressible flow.

F

luid

properties were considered as functions of temperature and

concan-tration of the foreign gas. The diffusion currents due to the

gradients of concentration and temperature were considered.

By

means

of the usual transformations, the system

reduced to a set of

.

ordinary differential equations, which in turn were transformed into

a set of integral equations and were solved by successive approximations.

The effects of thermal diffusion and diffusion thermo were neglected

in the whole analysis • Hydrogen and helium, both notable for their

low densities, high heat capacities and high specific heats were

considered

the isothermal (low speed) problem and helium alone

was considered in the case of compressible (hypersonic

)

flow. He

f

o

und that helium gas held great promise as a coolant in flight

regimes where aerodynamic heating was important. This result gave a

general idea of the effect of blo\nng even

w

ithout considering t

h

e

ef

f

ect of diffusion thermo.

Baron3 analysed the effect of thermal dif

f

usi

o

n

u

sing t

h

e

12

neglected

the

effect of

diffusion

He found that the

effect

of

thermal

diffusion on heat trans

fer was increased

·.nth

tC..e increase

of

injection of helium.

·

rhe

adiabatic

wall

for the

·

l!JiJ:ture

boundary layer

was

found to

be

40%

higher whan ther:1al diffusion

:;

as

considered than

when

it was neglected.

Eichhorn

44

,

studied the effects of blowing and suction of a

gas on the free convect

.

ion. flow heat transfer about a

vertical

plate.

The analysis

was

carried out under the condition

that

the buoyancy

forces

were due

only to temperature differences,

with

the mass transfer

entering the

problem

only as a prescribed flow

through the

surface.

He

considered the wall temperature as a function of

the

distance

from

leading edge of the plate, i.e.,

Tw -Too= Bx ,

where

B is a

constant.

order t-e

ha\re:

:

a

similar solution

-.

-Of

.

the laminar boundary layer equations,

he

needed to assume the

velocity (v ) across the plate to be a particular type

w

of the distance along the plate from the leading edge,

of

function

- (n

-1)/4

~.e.,

v

w

this

made his analysis very restrictive for the distributions

of

wall

temperature as well as for the blowing velocity. Also, the blowing

velocity distribution on the wall may be of any form for

theoretical analysis. But it is difficult to have any form of veloCity

distribution other than uniform velocity along the

wall

for experimental

purposes. Sparrow and

Cess~

used his similarity solution

and

extended

his

solution to a general form by using a

perturbation method. The

forms

were T -T-=Axn, v

=

Bxm,

where

nand m

~ay

be

chosen

independently. First two sets of equations

were

so_ved.

showed

in

their analysis that very small

or

suction

could

1

3

effect of

variable properties, thermal diffusion and diffusion

their

analysis could net

differentiate the effects of blowing or

suction

for different gases.

Gill et al4

6

analysed

the

combined

buoyancy

effects in

gaseous binary diffusion and included

the

effects

of varying transport

properties and species enthalpies while neglecting

the phenomena

of

species thermal diffusion and diffusion thermo.

This

study concerned

combined thermal and species diffusion in various

gases

like

hydrogen, water vapor, air, carbon

dioxide

into air

when

the

concen-trations of the species were comparable. The appropriate surface

condition of appreciable normal velocity

was

used.

i

,

:

umerical results

were

obtained

which

indicate the r.3lative i::1portance of

the

various

effects like the property variation due to temperature,

molecular weight

etc. The wall concentration

walL

_

temperature

_

were assumed to

-

he

_

constant.

-

So in order to transform

the governing

equations into ordinary equations, it was necessary

to

assume the

blowing velocity distribution to be of a particular form rather thm

uniform which made it difficult to achieve by experiments. It was also

found that the consideration of the variations of

properties

important in order to calculate the

heat

transfer rates, especially

when

the molecular weight of the blowing gas was very

much differen:t

than

that

of the boundary layer ga5. So

the

effects of thermal

diftusion

and

diffusion thermo would

also be important in

calculating the heat

transfer

rates.

Lowell

and

Adams47

considered

the

similarity solutions

for flat

plate with simultaneous

heat

and

mass transfer for rewtonian fluids

energy and

conservation

o: spec

_

ies eaq

.

a tio:::J.s. The li.:ni ta tions

·

Hera

,

the

same as

those

assumed by Gilr

46 ,

but

constant

properties

~ere

assumed.

The

boundary condition of appreciable

velocit

y

at

the

surface and

the

effects of comparable concentration levels

were

included.

The

only similarity condition

fot

:

nd was that

of an isothermal

surface.

Adama and Lowe11

48

solved the

non-I~near

partial

differential

equations defining free convection boundary layer flow along a

vertical, flat, subliming, nonreacting surface. The ambient temperature

and pressure were varied to observe the resulting effects on the

Ilusselt

and Sherwood numbers. Particular interest

was

directed to the effect

of the pressure ratio (ambient pressure to

v1all

pressure of sublimmg

component). The results indicated that there

was

an increasing effect

of the mass transfer upon heat transfer as the pressure ratio decreased.

Gardner and Hellums 49 considered

~he si~ultaneous

heat and

mass transfer in laminar free convection with a moving interface

using

the low species concentration level approximation. They analyzed the

flow adjacent to a liquid layer assuming this liquid surface

to be

isothermal. Interfacial velocity was taken into account and some

numerical results

were

presented. But the effects of

diffusion and diffusion thermo were not considered

here.

Recent

-

.·

ex-perimental

work

by Lewis et al' for the

,...o

study of natural convection mass transfer along a

vertical plate,

with

surface injection of

·

water into an aqueous

NaCl

solution

using a

Mach-Zehnder

interferometer

very

good agreement

with

their theoretical

prediction.

This agreement for concentration

distribution, Sc,

Gr

etc were found to be good at low injection