The Effects of Credit Risk and Funding on the Pricing of Uncollateralized Derivative Contracts
Full text
Figure
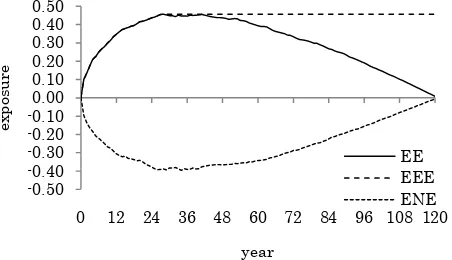


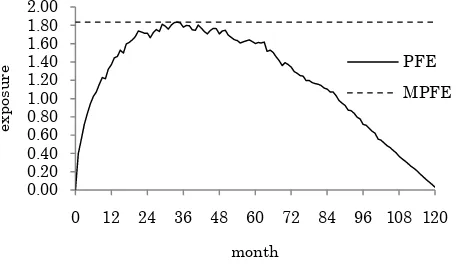
Related documents
The CMM model asks us to consider “what spe- cific meanings are (people) making in given situations, how are they making those meanings, and how those meanings affect the social
Mon Integrated Care (Center City) Tues Traditional MH (N Knox) Wed* (July-Mar) Traditional MH (N Knox) Wed* (Apr-July) Psychosoc Rehab (5 th St) Thurs Integrated Care
The proposed Peyton Slough Hydraulic Relief Project consists of removing an existing hydraulic restriction in Peyton Slough to improve water exchange between McNabney Marsh and Suisun
Field experiments were conducted at Ebonyi State University Research Farm during 2009 and 2010 farming seasons to evaluate the effect of intercropping maize with
Make sure the name on the box and the list match and ensure card is neatly attached, and check to see if the mail is over a semester old.. Check the name, make sure the card is
19% serve a county. Fourteen per cent of the centers provide service for adjoining states in addition to the states in which they are located; usually these adjoining states have
The 54 cases initiated by Dutch investors by end of 2012, represent 10 per cent of the global number of known cases and account for one-fifth of all claims filed by investors from
In short previous studies have shaped many aspects of the knowledge base in this part of the IS field ranging from success factors, implementation process,