Illumination Invariant Face Recognition Using Fuzzy LDA and FFNN
Full text
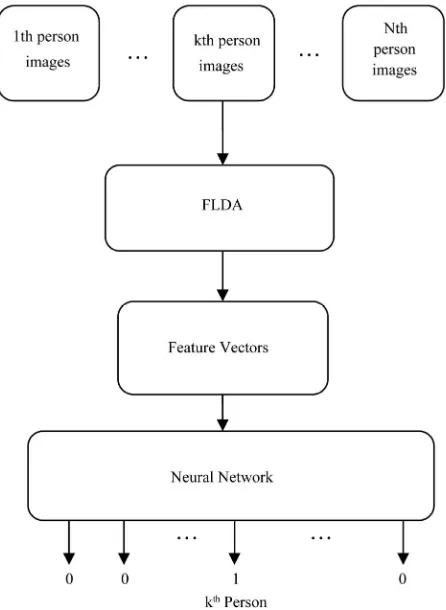
Figure


Related documents
This pilot study sought to develop and evaluate an online interface for primary care providers to refer patients to an Internet-mediated walking program called Stepping Up to
(2016), A power efficient cluster-based routing algorithm for wireless sensor networks: Honeybees swarm intelligence based approach, Journal of Network and
as potential biomarkers in patients with coronary heart disease and type 2 diabetes mellitus. [Epub ahead
ensure sandboxed apps are executed at each login, ‘legitimately’. L OGIN I TEMS (
12919 2018 126 Article 1 5 BMC ProceedingsWu et al BMC Proceedings 2018, 12(Suppl 9) 60https //doi org/10 1186/s12919 018 0126 9 PROCEEDINGS Open Access An adaptive gene based test
Troncoso Romero et al EURASIP Journal on Advances in Signal Processing 2014, 2014 122 http //asp eurasipjournals com/content/2014/1/122 RESEARCH Open Access On the inclusion of
In this case, both biaxial and unidirectional layers of glass fibre are bonded and then it is analysed using ANSYS .The total deformation and the equivalent stress are given