A Multi-objective Approach for Multi-commodity Location within Distribution Network Design Problem
Full text
Figure


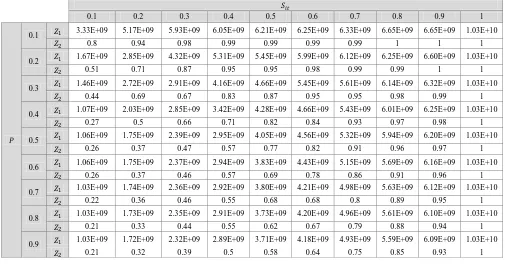
Related documents
Key PHO relationships are with DHBs, other PHOs, management services organisations (MSOs) and other agencies in the community. In the Survey of
In his essay “Should Kids Compete in Mixed Martial Arts (MMA) Bouts?” Mike Adams contends that practicing Mixed Martial Arts is far less dangerous for children than 5
To our knowledge, this is the first study to examine consolidation in infants’ self-regulated nocturnal sleep as judged by 3 different criteria for sleep- ing through the night and
Effective 12/04/07, the Commercial or Music Video Production Company (hereafter “Company”) must file its final report from its CPA to the Governor‟s Office of Film and
Three deficiencies in particular should be mentioned: (i) the existing mechanical models of high-angle water injection wells have not taken comprehensive account
recommendation was significantly poorer than that of the basic matrix collaborative filtering algorithm and the probability matrix decomposition collaborative filtering
The double tube cooler is made of 1/2” (12,7 mm) primary tubes with a circuit specifically sized for the conditions of the cooling water.. The pair of tubes are mounted in a bundle
While one application is the retrieval of documents that support extracted infor- mation to verify the correctness of the piece of information, another application in combination