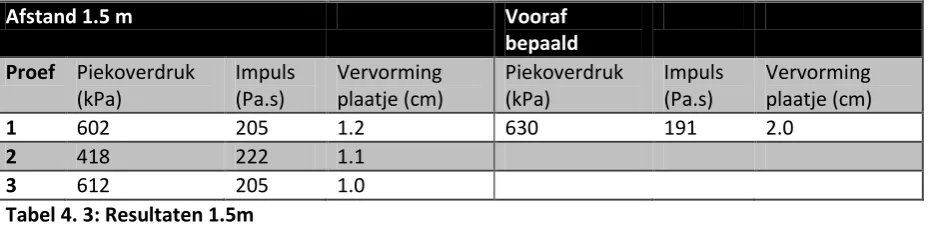
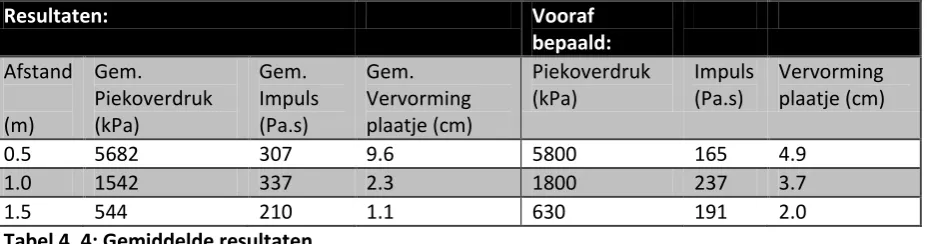
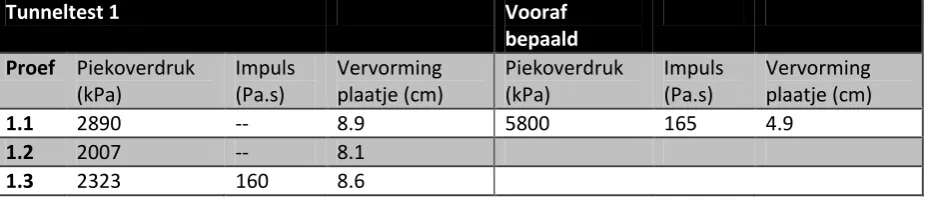
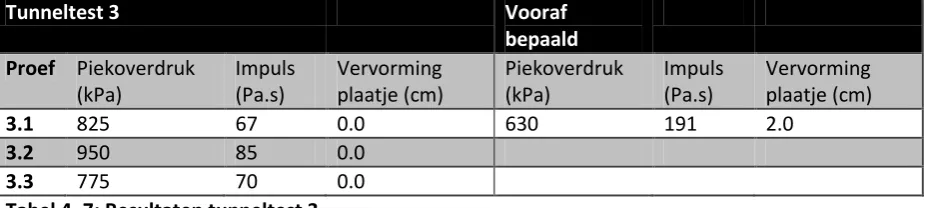
Validatie van een schalingsmethode: Een onderzoek naar een vernieuwende methode op het gebied van het terugschalen van explosies
Full text
Figure

Related documents
Figure 21: Throughput of Receiving Bits vs Average Simulation Processing Time of Efficient AODV.. Further, neither there is any suggestion how to use it nor is it
Other genetic endocrine syndromes associated with pi- tuitary tumors are the familial isolated pituitary adenoma (FIPA) syndrome (of which AIP mutations are a subset),
The RESPONSES are, from the energy point of view, the “sustainable energy targets” that determine actions for energy saving and conservation, efficiency and production from
Respon· sibilities include conceptual definition and design of the date base(s); establishment of data base related standards, procedures and methodologies; data base
In 1982; Wyly strengthened its sys- tems software business, which serves IBM and IBM-compatible data centers. Introduced were vcc Seven BASIC, an expansion of its
All insertion events for a given transposon were used to generate BLogo sequence logo plots of position speci- fic sequence bias, with positions colored if significant at P <
We have selected Maritigrella crozieri , the tiger flatworm, as a suitable polyclad species for developmental studies, because it is abundant and large in size compared to
The results of the two stages used in industrial wastewater treatment were identical with the Egyptian standards for reusing the treated dairy wastewater in irrigation purposes..