RESEARCH PAPER
Available Online at http://www.journalofcomputerscience.com/
A Randomized Searching Algorithm and its
Performance analysis with Binary Search and
Linear Search Algorithms
Pranesh Das(M.Tech)
Department of Computer Science and Engineering National Institute of Technology Rourkela
Rourkela ,India pranesh.das@gmail.com Prof. Pabitra Mohan Khilar
Department of Computer Science and Engineering National Institute of Technology Rourkela
Rourkela,India pmkhilar@nitrkl.ac.in
Abstract
Design and Analysis of Algorithm is one of the most important areas of Computer Science and Engineering.Searching and Sorting Algorithms play a key rule here.Research conducted over the past fifteen years has amply demonstrated the advantages of algorithms that make random choices in the course of their execution. We have various Searching Algorithms available.In this paper we have proposed a Randomized Searching Algorithm and then performance analysis is done between the proposed Algorithm and the existing Binary Search and Linear Search Algorithms. The performance of the Proposed Algorithm lies between Binary Search and Linear Search.
Keywords-
algorithm, complexity analysis, binary search, linear search.1.
Introduction
A randomized algorithm is one that receives, in addition to its input data, a stream of random bits that it can use for the purpose of making random choices. Even for a fixed input, different runs of a randomized algorithm [2] may give different results; thus it is inevitable that a description of the properties of a randomized algorithm will involve probabilistic statements. For example, even when the input is fixed, the execution time of a randomized algorithm is a random variable. There are two principal types of advantages that randomized algorithms often have. First, often the execution time or space requirement of a randomized algorithm is smaller than that of the best deterministic algorithm that we know of for the same problem. But even more strikingly, if we look at the various randomized algorithms [2] that have been invented, we find that invariably they are extremely simple to understand and to implement; often, the introduction of randomization suffices to convert a simple and naive deterministic algorithm with bad worst-case behaviour into a randomized algorithm that performs well with high probability on every possible input. In our proposed Randomized
Searching Algorithm we choose a position randomly in each iteration and then the element of that position is compared with the key item. The organization of the paper is as follows: section 2 presents the related work, section 3 presents the proposed RSA algorithm and section 4 presents about performance analysis of the proposed RSA algorithm with the existing Binary Search and Linear Search Algorithms.
2.
Related Work
Searching an item or data from a large data set efficiently gives a challenging task.There are number of searching algorithms available like Binary Search, Linear Search, DFS,BFS,BST etc. The studies on searching have been carried out by Francesc [1],Robert [3] , Bharat [4], Ziqiang[5] and so on. Binary Search provides a very good performance with respect to other algorithms but in this case every time we need to calculate the mid position .Instead of this in our proposed RSA we choose a position randomly and compare it with the key item because randomization improves the performance of an algorithm [2].
3.
Proposed Randomized Searching Algorithm
3.1. Description In our proposed Randomized Searching Algorithm the main idea is to select positions randomly from the sorted input array and compare elements of those positions with the search key until the match is found or the array is finished. If the key element is found in the randomly selected position p then we stop. If the search key is less than or greater than the element of the chosen position then the searching is continued in the left side or in the right sight of the position respectively. We have done the simulation in MATLAB 7.12.0(R2011a).We have generated the elements of the input array A randomly. We also have generated the search key element K randomly and done the simulation for a large no of times with arrays of different sizes.
3.2. Working of the proposed RSA
4.1.1. Complexity Analysis We see that in the first two lines of the working of the proposed RSA before the while loop, 2 primitive operations always get executed (two assignments). However, since these operations happen no matter what the input is, we will ignore them for now. Focusing our attention on the while loop, we see that each time the program enters the while loop, we execute 3+k primitive operations (a <=comparison, k number of operations to choose a random number between lb and ub, an array index, and a < comparison), before the program might branch depending on the result of the first if statement.
Depending on the result of the conditional, the program will execute different numbers of primitive operations. If key > A[p] (A is the sorted input array) , then the program executes 2 more primitive operations. If key <A[p], then the program executes 4 more primitive operations (an array index and a <comparison in the next if, and then a subtraction and assignment). If A[p] = = key, then we execute 3 more primitive operations (2 operations for the if and then 1 operation to return position p). As k is fix for each iteration so we neglect k now. In other words, the number of primitive operations executed in an iteration of the loop is
5, if key < A[p]
6 , if A[p] = = key, and 7 , if key > A[P].
We can now construct a tree that summarizes how many operations are executed in the while loop, depending on the number of times the while loop is executed and the result of the comparisons between A[p] and key in each iteration. Each node in the tree represents the exit from the algorithm because A[p] = = key. A node is a left child of its parent if in the previous iteration of the while loop, the search was restricted to the left part of the sub array (that is, when A[P] > key). A node is a right child of its parent if in the previous iteration of the while loop, the search was restricted to the right part of the sub array (that is, when A[p] <key). Here are the first three levels of the tree:
Figure 1: No. of operations as a tree structure
In case of Binary Search algorithm height of the left sub tree and the height of the right sub tree are equal and we can easily proof that the average case time complexity [1] for binary search is log n. Because the number of nodes are equal in both the left and right sub trees and total number of nodes on each level can be easily computed. But in our proposed algorithm as the position is randomly chosen so the height of left sub tree and the height of right sub tree may not be equal.
Hence to analyse the average case behaviour we have done a simulation on our proposed algorithm. We have done the simulation on the basis of number of elements versus number of comparisons instead of number operations. In our described algorithm on section 3.2 the
relevant number of comparisons (one <= comparison, one < and one >) executed in an iteration of the loop is:
2, if key < A[p] 3, if A[p] = = key, and 3, if key > A[P].
We have simulated the proposed algorithm in MATLAB 7.12.0(R2011a).In the simulation we have generated the elements of the arrays randomly and also the key. The simulation is done for 50 times with different number of elements ranges from 10 to 500.The simulated result for average case is shown below:
Table 1: Simulated Result for Average Case (no.of elements and no.of comparisons) No.of eleme nts No.of compa risons No.of eleme nts No.of compa risons No.o f elem ents No.of compa risons No.of elem ents No.of compar isons No.of element s No.of comp ariso ns 10 7 110 14 210 24 310 22 410 19 20 14 120 18 220 17 320 29 420 22 30 20 130 18 230 30 330 22 430 19 40 12 140 24 240 41 340 25 440 16 50 24 150 25 250 18 350 28 450 24 60 8 160 32 260 21 360 19 460 32 70 12 170 20 270 22 370 33 470 23 80 33 180 23 280 15 380 30 480 29 90 26 190 23 290 18 390 30 490 39 100 25 200 28 300 19 400 15 500 25
From the above table Table1 we see that in average approximately 3log n (base 2) comparisons are required to find the key item for the different set of elements. Hence we can say that approximately the time complexity of our proposed Randomized Searching Algorithm is O(3log n) in Average Case.
For Best Case every time we find the key in the first attempt i.e. in the first loop and only 3 comparisons are performed for every set of elements.
In Worst Case key item is not in the input array i.e. in every iteration maximum number of comparisons are performed. The simulation is done in MATLAB 7.12.0(R2011a) for the worst case analysis. Here also we have generated the keys and the elements randomly and done the simulation for 50 times with different number of elements ranges from 10 to 500.The simulated result for Worst Case is shown below:
No.o f elem ents No.o f com paris ons No.of eleme nts No.of compa risons No.of eleme nts No.of compa risons No.of eleme nts No.of compa risons No.of eleme nts No.of compa risons 10 9 110 27 210 31 310 21 410 45 20 18 120 20 220 23 320 24 420 21 30 10 130 14 230 14 330 26 430 26 40 18 140 20 240 20 340 21 440 24 50 16 150 10 250 25 350 20 450 31 60 27 160 22 260 26 360 38 460 21 70 16 170 19 270 26 370 28 470 27 80 18 180 32 280 22 380 23 480 12 90 20 190 13 290 29 390 15 490 18 100 15 200 14 300 25 400 15 500 28 From the above table Table2 we observe that approximately in average the same numbers of comparisons are required to find the key items for the different set of elements as like as the average case. Hence we can say that in Worst Case also approximately the time complexity is O(3 log n) .
4.1.2
Efficiency Graphs Compared to Binary Search and Linear Search Algorithms
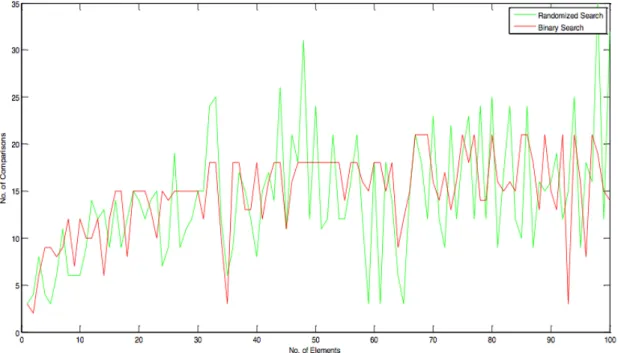
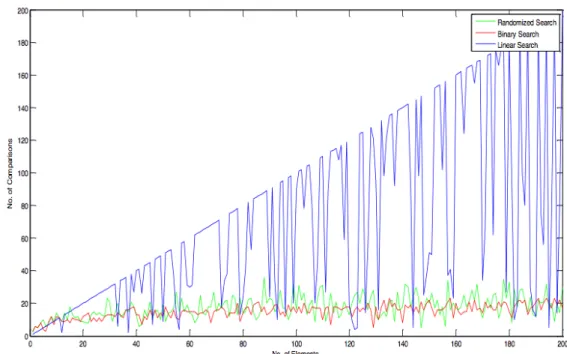
Here we have shown the performance analysis of our proposed algorithm graphically. In figure 2 we see that our Proposed Algorithm is performing approximately same as Binary Search in average case. During simulation it is seen that some times our proposed algorithm gives better result then the Binary Search. Here we did not get smooth graph because of randomization. From figure 3 we see that our proposed algorithm is giving better result then the existing linear Search Algorithm (although linear search is applied on unsorted array). In figure 4 average case behaviour of Linear Search, Binary Search and RSA is shown. In figure 5 worst case analysis is done. It is seen that average case and worst behaviour are nearly same for our Proposed RSA Algorithm.
Figure 2: Average Case behaviour of the proposed RSA and the existing Binary Search Algorithm
Figure 3: Average Case Behaviour of the Proposed RSA and the existing Linear Search Algorithm
Figure 4: Average Case Performance Analysis of the Proposed RSA, Binary Search and Linear Search Algorithms.
Figure 5: Worst Case Behaviour of the Proposed Randomized Search Algorithm (RSA) and the existing Binary Search Algorithm.
5.
Conclusion
Performance of the proposed RSA algorithm lies between Binary Search and Linear Search Algorithms. With respect to Linear Search our algorithm gives better performance although Linear Search is applied on unsorted data. Due to randomization we can get an average result every time. We will improve the performance of the algorithm by designing a proper algorithm to choose a number randomly.
References
[1] Francesc J. Ferri and Enrique Vidal, Case-Studies on Average-Case Analysis for an
Elementary Course on Algorithms, IEEE TRANSACTIONS ON EDUCATION, VOL. 42, NO. 2, MAY 1999.
[2] Karp, R.M., An introduction to randomized algorithms, Discrete Applied Mathematics, Computer Science Division, University of California Berkeley, International Computer
Science Institute, Berkeley, CA 94704, USA .
[3] Robert Nowak,Generalized Binary Search,Forty-Sixth Annual Allerton Conference Allerton House, UIUC, Illinois, USA September 23-26, 2008.
[4] Bharat Singh, Ishadutta Yadav, Suneeta Agarwal, Rajesh Prasad, An Efficient Word Searching Algorithm through Splitting and Hashing the Offline Text,2009 International Conference on Advances in Recent Technologies in Communication and Computing, IEEE Explore.
[5] Ziqiang YU, Xianqiang Liu,Improvement of Dynamic Binary Search Algorithm
Used in RFID System,2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference.