Adaptive mechanism design and game theoretic analysis of auction driven dynamic spectrum access in cognitive radio networks
Full text
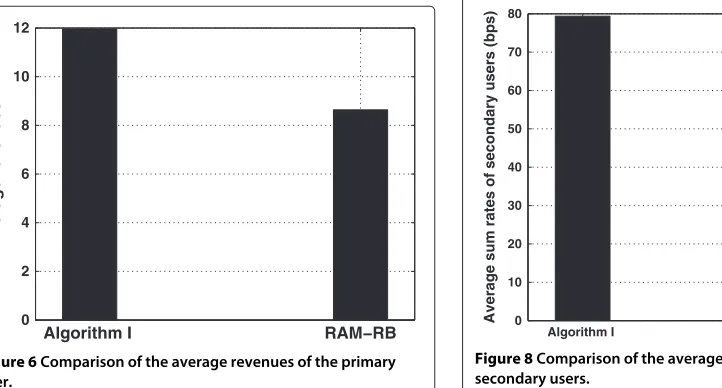
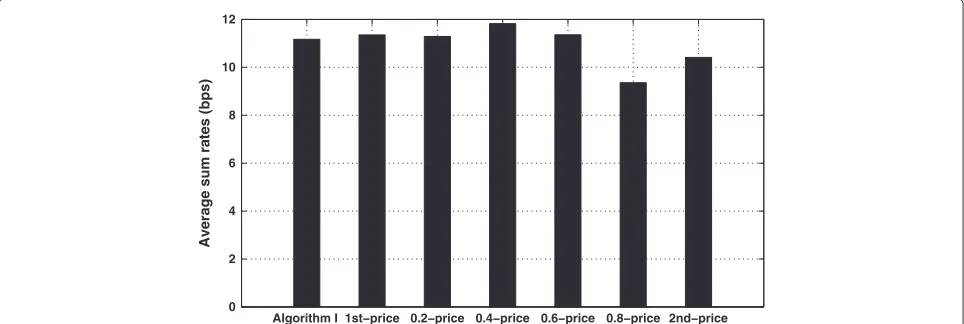
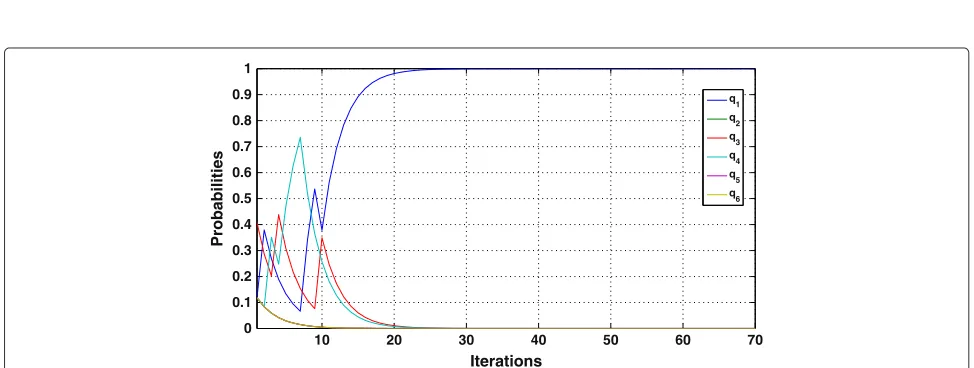
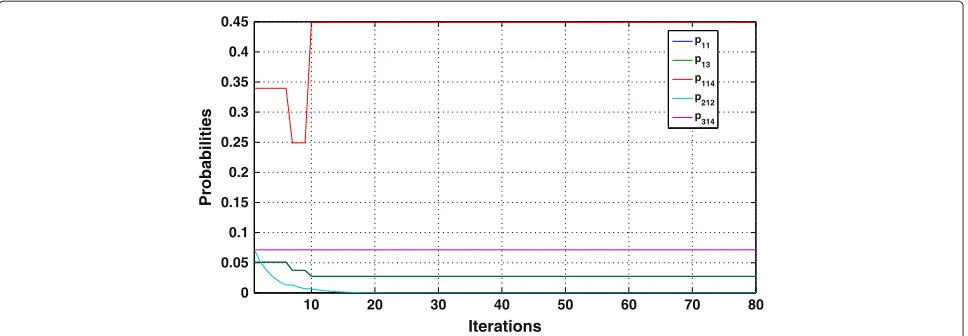
Figure
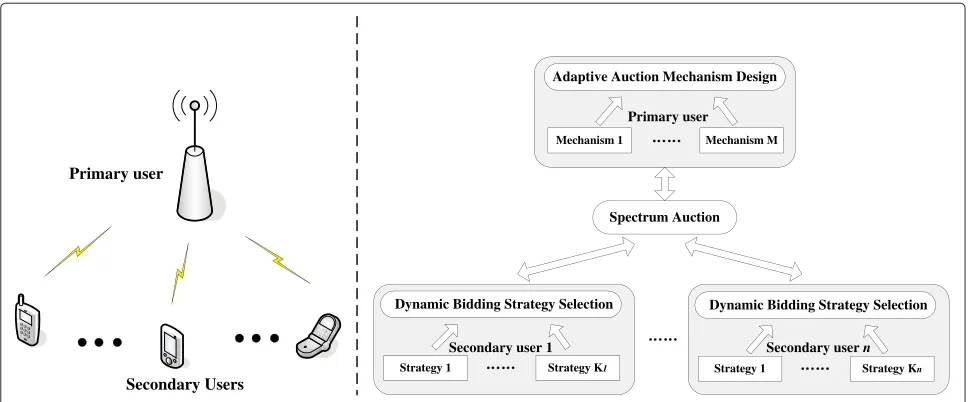

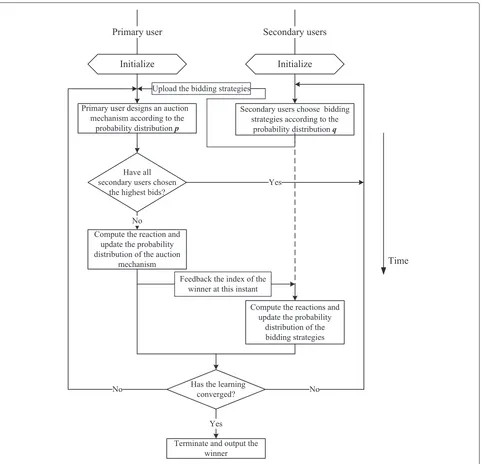
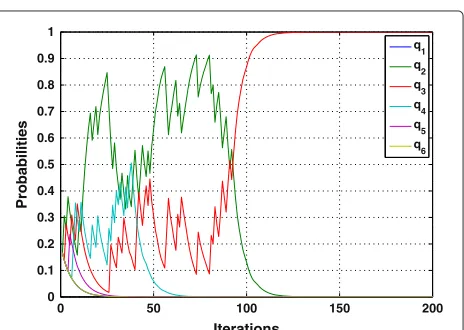
Related documents
The impact of HIV/AIDS on growth rates of life expectancy is calculated as the difference in growth rates between the estim ates of actual life expectancy and the
Google Scholar was used to identify the 100 most highly cited articles published in academic peer-reviewed journals. To identify relevant articles, searches
For my research thesis I am hoping to conduct a piece of action research into using solution focussed therapeutic approaches with children with learning difficulties. I am writing
Furthermore, it can explain why “government contracts with nonprofits often include as a standard feature pricing be low cost (Miller, 2006).” The results also
examined to explore the influence of the family context on the child’s adaptation to primary school (Cowan, Cowan, Ablow, Johnson, & Measelle, 2013) but the actual experience
The aim of this study is to explore the experiences of IAPT high intensity therapists delivering cognitive behavioural therapy (CBT) to clients with a
The purpose of this qualitative study was to explore the major areas of psychosocial concerns, individual anxieties and coping responses for fathers with
RadioActive Europe: promoting engage- ment, informal learning and employability of at risk and excluded people across Eu- rope through internet radio and social media