Fpga implementation of Floating-Point Arithmetic

(1)

Fpga implementation of Floating-Point Arithmetic

Ajay Rathor, Prof. Lalit Bandil

Department of Electronics & Telecommunication Engg. Acropolis Institute of Technology and science indore, India

,

Abstract

Floating point arithmetic fpga implementation described various arithmetic operations like addition, subtraction, multiplication, division. Floating point fpga arithmetic unit are useful for single precision and double precision and quad precision .This precision specify various bit of operation. In science computation this circuit is useful. A general purpose arithmetic unit require for all operations. In this paper single precision floating point arithmetic calculation is described. This paper includes single precision, double precision and quad precision floating point format representation and provide implementation technique of various arithmetic calculation. Double precision and quad precision format specify more bit operation. Low precision custom format is useful for reduce the associated circuit costs and increasing their speed. Fpga implementation of Floating point arithmetic calculation provide various step which are require for calculation. Normalization and alignment are useful for operation and floating point number should be normalized before any calculation. I consider the implementation of 64/ 128-bit precision circuits.

Keywords: FPGA implementation, single precision, doubles precision, quad precision VERILOG HDL

1. Introduction

Floating point arithmetic unit with fpga implementation are useful for various common operations i.e. addition/subtraction, multiplication, division. This is invaluable tools in the implementation of high performance systems, combining the reprogrammability advantage of general purpose processors with the speed and parallel processing. At some point, require general purpose arithmetic processing units which are not standard components of fpga devices. Implementation of operators in low precision custom format in order to reduce the associated circuit costs and increase their speed. More recently, the increasing size of fpga devices allowed researchers to efficiently implement operators in the 32-bit single precision format. Double precision and quad precision described more bit operation so at same time we perform 32 and 64 bit of operation of arithmetic unit.

2. Floating Point format Representation

Floating point number has mainly three formats which are single precision, double precision and quad precision.

(2)

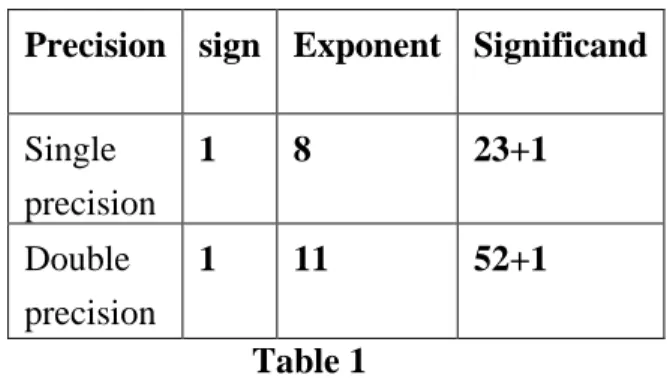
Dynamic range of values by using a floating point. As mentioned in Table 1 the single precision format has 23 bits for significand (1 represents implied bit), 8 bits for exponent and 1 bit for sign.

The IEEE standard specifies that Single precision floating-point numbers are comprised of 32 bits, i.e. a sign bit (bit 31), 8 bits for the exponent E (bits 30 down to 23) and 23 bits for the fraction f (bits 22 to 0). E is an unsigned biased number and the true exponent e is obtained as e=E–Ebias with Ebias=127 the leading 1 of the significand, is commonly referred to as the “hidden bit”. This is usually made explicit for operations, a process usually referred to as “unpacking”.

Double Precision Format: The IEEE standard specifies that double precision floating-point numbers are comprised of 64 bits, i.e. a sign bit (bit 63), 11 bits for the exponent E (bits 62 down to 52) and 52 bits for the fraction f (bits 51 to 0). E is an unsigned biased number and the true exponent e is obtained as e=E–Ebias with Ebias=1023. The fraction f represents a number in the range [0,1) and the significand S is given by S=1.f and is in the range [1,2).The leading 1 of the significand, is commonly referred to as the “hidden bit”. The range of the unbiased exponent e is [1022, 1023], which translates to a range of only [1, 2046] for the biased exponent E. The values E=0 and E=2047 are reserved for special quantities. The number zero is represented with E=0, and f=0.

Quad Precision Format:The IEEE standard specifies that double precision floating-point numbers are comprised of 128 bits, i.e. a sign bit (bit 127), 15 bits for the exponent E (bits 126 down to 112) and 112 bits for the fraction f (bits 111 to 0). E is an unsigned biased number and the true exponent e is obtained as e=E–Ebias with Ebias=16383.

Table 1

Table 1 show single precision and double precision floating point number specification. Single precision for 32 bit and double precision for 64 bit used different exponent and significand. Quad precision format used for 128 bit and described different significand and exponent.

3. Addition/Subtraction

If two numbers x and y which described floating point numbers and we perform calculation sum or difference of two numbers. Firstly, we check for zero of two values and then require next step calculate the difference of the two exponents, so need operation of alignment. Align the significand Ex–Ey =0 and put exponent ER is result of the two exponents. Now add or subtract the two significands Ex and Ey, according to the effective operation. Normalize the result SR, adjusting ER as appropriate. Step by step we can perform addition and subtraction of two floating point numbers.

In the first step, the floating point operands x

and y are unpacked and checks for zero, infinity. If we can assume that neither operand is infinity. The relation between the two operands xand y is determined based on the relation between Ex and Ey and by comparing the significands sxand sy, which is required if Ex=Ey. Swapping Sx and Sy is equivalent to swapping x and y and making Precision sign Exponent Significand

Single

precision

1 8 23+1

Double

precision

(3)

an adjustment to the sign sr. this swapping requires only multiplexers

Block diagram of a floating-point adder/subtractor

In the next step, alignment of two significand used. The significand alignment shift is performed and the effective operation is carried out. This step useful for

equal the significand numbers. Alignment achieved by shifting either smaller number to right. Now we can say that increasing it exponent .if alignment has been completed then we go for next step normalization. Alignment is useful for next step of normalization. Without this step result not be calculated.

Normalization is last step for floating point arithmetic operation. Sr is normalized by after the alignment and shifter, which can perform by right shifts. If sr is normalized, then it shows result of two floating point number of addition and subtraction.

Addition and subtraction of two floating point number described in following block diagram. Step by step we perform calculation of two floating point number addition and subtraction. Firstly if we taken two floating point number for addition and subtraction then in starting both number will be unpack. After that we identify sign, exponent and significand of both numbers. This process depends on single precision and double precision and quad precision format. According to this format we taken sign, exponent and significand bit. The IEEE standard specifies that format.

Normalization process will be completed after specify IEEE standard. In this step normalize the number means move binary point so that it is one bit from left. Shifting the mantissa left by one bit decrease the exponent by one or shifting the mantissa right by one bit increases the exponent by one. Before subtracting, compare magnitude and change sign bit if order of operands is changed .Alignment can be done after that process and finally we get result of addition and subtraction of two floating point numbers.

4. Multiplication

Two Floating point number calculation can be perform by adding exponent of two numbers and multiply significand of two

Normalize

Add

Align significands

Unpack

k

Control l & sign sign logic c Add/ / Sub b

Pack

k

Operands

s

Sum/Difference

Significands s Exponents s Signs s Significand d Exponent t Sign n

A

B

s

Sub b Add d Mux x

c

out t Selective complement and possible swap

Round and

Selective complement

Normalize

(4)

numbers. The product R of two numbers A and B are as follows. Calculate the exponent of the result as Ez=Ex+Ey–Ebias. Multiply Sx and Sy to obtain the significand Sz of the result. Normalize Sz, adjusting Ez as appropriate, and Ez to be readjusted. After addition and subtraction, multiplication is the most frequent operation in scientific computing.

In the first step , the operands x and y are unpacked and checks are performed for zero, infinity. For now we can assume that neither operand is zero, infinity. The sign sz of the result is easily determined as the XOR of the signs sx and sy. From this point, x and y can be considered positive. As the first step in the calculation of Ez, the sum Ex+Ey is calculated using a fast ripple-carry adder. In the second step, the excess bias is removed from EA+EB using the same adder .The result of this addition is the final normalized .double precision floating point number consider exponent 11bit and significand 52 bit for multiplication of two numbers. After normalization exponent change to bias form. The result Ez will be readjusted. Increment by 1 can be performing in the processing adder. Multiplication of two floating point number can be explained in following bock diagram. Firstly input data will be unpack and then multiply significand and add exponent operation will be performed. Control and sign logic used for control the operation. And finally normalization process will be used for two numbers. Step by step we perform this process and show result of two floating point numbers. First number can be consider multiplier and second can be multiplicand. Overflow and underflow can occur during multiplication and normalization .If the exponent of the product is with in the proper range, the next step is to multiply the significands. After that we get result.

Block diagram of floating point multipliers

5. Division

Calculation of division of two floating point numbers can be easily understood by block diagram of floating point divider. The calculation of the quotient R of two numbers x (the dividend) and y (the divisor) are as follows. Calculate the exponent of the result as Ez=Ex–Ey+Ebias. Divide Sx by Sy to obtain the significand Sz. In the first step the operands A and B are unpacked for now; we

XOR Add

Exponents Unpack

Normalize Adjust

Exponent

Round

Normalize

Pack

Multiply Significands

Floating-point operands

Product

(5)

can assume that neither operand is zero, infinity. The sign sz of the result is the XOR of sx and sy,. For the calculation of Ez, the difference Ex–Ey is calculated using a fast ripple-carry adder. After normalization result of two floating point number can be show division of two numbers.

Block diagram of floating point divider

In the division process first step is testing for zero. A dividend of zero result in zero. Next the divisor exponent is subtracted from the

Dividend exponent. This removes the bias, which must be added back in. Tests are then made for exponent underflow or overflow. The next step is to divide the significands. It is followed with the usual normalization. The hardware implementation of floating-point operations involves a considerable amount of logic circuitry. The sign of the difference that results from comparing exponents determines which mantissa is to be shifted. After divide mantissa and subtract exponent then normalize the result. Left shift result, decrement result exponent and right shift result, increment result exponent will be performed. If larger/smaller than maximum exponent allowed return exponent overflow/underflow. After normalization result of two floating point number can be show division of two floating point numbers.

6.

Result and discussion

The implementation of floating point addition of two number on FPGA described in simulation report. This is low cost FPGA floating-point arithmetic circuits in the 64-bit double precision format and for all the common operations. Simulation report explains result of addition of two floating point number. We can perform addition subtraction multiplication and division of two floating point number which can be single precision, double precision and quad Precision. A direct comparison with other floating-point unit implementations is very difficult to perform, not only because of floating-point format differences, but also due to other circuit characteristics, e.g. all the circuits presented here incorporate I/O registers, which would eventually be absorbed by the surrounding hardware. In

XOR Subtract

Exponents Unpack

Normalize Adjust

Exponent

Round

Normalize

Pack

Divide Significands

Floating-point operands

Quotient

(6)

conclusion, the circuits presented here provide an indication of the costs of FPGA floating-point operators using a long format. Two floating point number A and B shows input data. And we get result in C which is result or output. This is shown in simulation waveform. This figure show single precision addition of two floating point numbers. In this implementation use clock pulse and load pulse for getting result. Load pulse applies initially when positive edge triggers clock pulse stating. Resets also apply for new calculation. In this result single precision 32

bit calculation shows. If we used double precision then used 64 bit and for quad precision used 128 bit calculation of data. Similarly we get result of subtraction and multiplication and division of two floating point numbers.

(7)

[1] B. J. Hickmann, A. Krioukov, M. A. Erle, and M. J. Schulte, “A Parallel IEEE P754 Decimal Floating-Point Multiplier,” in 25th IEEE International Conference on Computer Design. IEEE Computer Society, October 2007, pp. 296–303

.

[2] M. F. Cowlishaw, “Decimal Floating-Point: Algorism for Computers,” in 16th IEEE Symposium on Computer Arithmetic. IEEE Computer Society, June 2003, pp. 104–111.

[3] ANSI/IEEE STD 754-1985, “IEEE Standard for Binary Floating-Point Arithmetic”1985.

[4] Loucas, L., Cook, T.A., Johnson, W.H., “Implementation of IEEE Single Precision Floating Point Addition and Multiplication on FPGAs”, InProc. IEEE Symposium on FPGAs for Custom Computing Machines, 1999.

[5] Belanovic. P., Leeser, M., “A Library of Parameterized Floating-Point Modules and Their Use”, In Proc. Field Programmable Logic and Applications, 2002, pp. 657-666.

[6] Shirazi, N., Walters, A., Athanas, P., “Quantitative Analysis of Floating Point Arithmetic on FPGA Based Custom Computing Machines”, In Proc. IEEE Symposium on FPGAs for Custom Computing Machines 1995, pp. 155-162.

[7] Li, Y., Chu, W., “Implementation of Single Precision Floating Point Square Root on FPGAs”, In Proc. 5th

IEEE Symposium On Field Programmable Custom Computing Machines 1997, pp. 226-232.

Scientist Should Know About Floating-Point Arithmetic”, ACM Computing Surveys.