The Study of Effect of Length in Morphological Segmentation of Agglutinative Languages
Full text
Figure
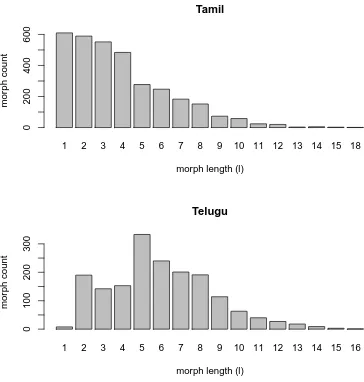
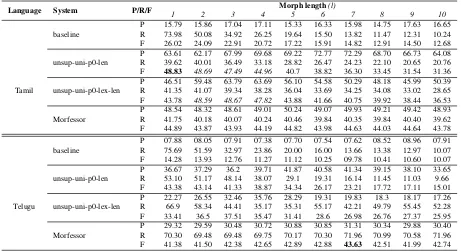
Related documents
Nilotinib therapy after dasatinib failure in patients with imatinib-resistant or -intolerant chronic myeloid leukemia (CML) in chronic phase (CP), accelerated phase (AP) or blast
Pertaining to the secondary hypothesis, part 1, whether citalopram administration could raise ACTH levels in both alcohol-dependent patients and controls, no significant
We show that by linking two factorization techniques often employed to solve Schroedinger’s equation one can give any one-dimensional hamiltonian the same form in terms of
Barriers and facilitators to engagement and recruitment to digital health interventions: protocol of a systematic review of qualitative studies. Tong A, Sainsbury P,
Graphs showing the percentage change in epithelial expression of the pro-apoptotic markers Bad and Bak; the anti-apoptotic marker Bcl-2; the death receptor Fas; the caspase
was associated with lower physical quality of life among earthquake and flood survivors in Iran and China, [26, 56] lower physical functioning in Iran, Rwanda, and Syrian refugees
We compared NOSM UGs and PGs with the full popula- tion of College of Family Physicians of Canada (CFPC)- certified physicians who completed UG education at a Canadian medical
The separations from the source vertex to the neighboring vertices are then refreshed in the program information structures, after which the calculation rehashes for the