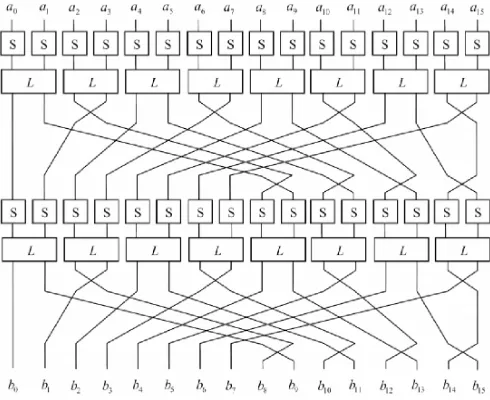
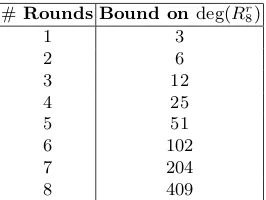
On the influence of the algebraic degree of $F^{−1}$ on the algebraic degree of $G \circ F$
Full text
Figure
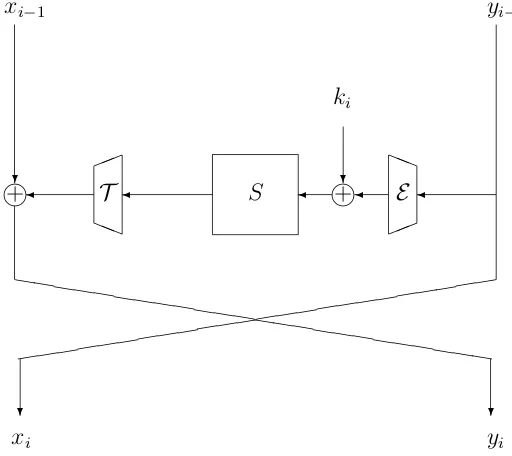
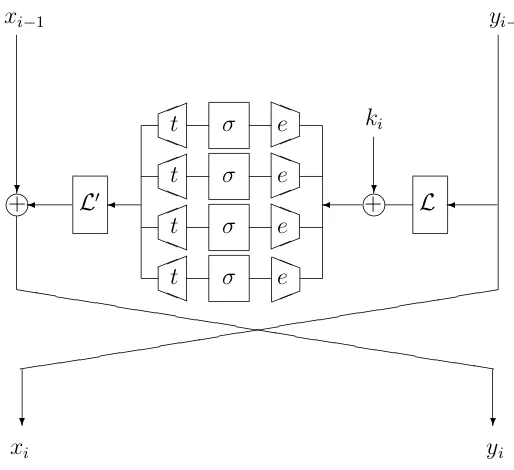
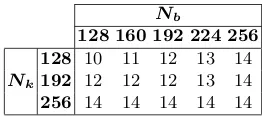
Related documents
It makes sense to consider four different pay regimes, each corresponding to work done at different times: Regular hours, 7AM-8PM Monday-Friday, with no wage penalty; night
Many studies of biped walking utilized the so- called ZMP criterion [2]–[5]: the reference trajectories of each joint angle, or the center of mass (CoM) of the body, are
The discovery of a role for the TWIK-related spinal cord potassium channel (TRESK) in migraine, in parti- cular resurrects the debate over the relative importance of peripheral
K Vijay Kumar HR Head Continuum Solutions Pvt Ltd (Bank Of America) Mr.. Puneet Makhija
This output type activates when the control panel Bell tamper or an expander input (programmed as Bell tamper) is activated, causing a Tamper alarm on the system, and
- CU AC Panel Mains reinstated + CU AC> Mains loss signalled - CU AC> Mains restored signalled + PSU AC Remote PSU Mains fault - PSU AC Remote PSU mains reinstated +PSU
In census data, it is identi fi ed by a steeply decreasing proportion of women with six or more children from the 1860 cohorts onwards in Croatia, Slovenia, and Serbia, while
In terms of haematopoietic stem cell (HPC) transplantation, there is an increase in both the absolute number of cord blood samples used for transplant, and the