Abstract
CHEN, JUNLIANG. A Monte Carlo EM algorithm for generalized linear mixed models
with flexible random effects distribution. (Under the direction of Daowen Zhang and Marie
Davidian)
A popular way to model correlated binary, count, or other data arising in clinical trials
and epidemiological studies of cancer and other diseases is by using generalized linear mixed
models (GLMMs), which acknowledge correlation through incorporation of random effects.
A standard model assumption is that the random effects follow a parametric family such
as the normal distribution. However, this may be unrealistic or too restrictive to represent
the data, raising concern over the validity of inferences both on fixed and random effects if
it is violated.
Here we use the seminonparametric (SNP) approach (Davidian and Gallant 1992, 1993)
to model the random effects, which relaxes the normality assumption and just requires that
the distribution of random effects belong to a class of “smooth” densities given by Gallant
and Nychka (1987). This representation allows the density of random effects to be very
flexible, including densities that are skewed, multi–modal, fat– or thin–tailed relative to
representation to avoid numerical instability in estimating the polynomial coefficients.
Because an efficient algorithm to sample from a SNP density is available, we propose
a Monte Carlo expectation maximization (MCEM) algorithm using a rejection sampling
scheme (Booth and Hobert, 1999) to estimate the fixed parameters of the linear predictor,
variance components and the SNP density. A strategy of choosing the degree of flexibility
required for the SNP density is also proposed. We illustrate the methods by application
to two data sets from the Framingham and Six Cities Studies, and present simulations
A MONTE CARLO EM ALGORITHM FOR
GENERALIZED LINEAR MIXED MODELS WITH
FLEXIBLE RANDOM EFFECTS DISTRIBUTION
by
JUNLIANG CHEN
A dissertation submitted to the Graduate Faculty of North Carolina State University
in partial fulfillment of the requirements for the Degree of
Doctor of Philosophy
STATISTICS
Raleigh
2001
approved by:
Dennis D. Boos Sujit Ghosh
Daowen Zhang Marie Davidian
Biography
CHEN, JUNLIANG was born on September 22, 1972 in Huangmei, Hubei province, P.R.China.
He entered the Department of Mathematics at Nankai University in Tianjin, P.R.China in
1991, and received a B.S. degree in Mathematical Statistics there in 1995. After two years
graduate study, he decided to join the graduate program in Statistics at North Carolina
State University in August 1997. He earned his M.S. in Statistics in 1999 and continued
Acknowledgments
First of all, I would like to express my deepest appreciation to my advisors, Dr. Daowen
Zhang and Dr. Marie Davidian, for their guidance, encouragement and patience throughout
the development of my doctoral research and the preparation of my thesis. I would also
like to thank the rest of my advisory committee for their review of this work and many
valuable suggestions.
I gratefully acknowledge the Faculty in Statistics at North Carolina State University
for their high quality instruction and guidance. I thank my friends, including my fellow
graduate students and my fellow statisticians at SAS, for their assistance and friendship.
Finally, I thank all of my family, including my in–laws, for their support through this
process. I especially want to thank my wife Lihua for her love, encouragement, support
and patience, and my daughter Jessica who gave me so much pleasure during the course of
Table of Contents
List of Tables vii
List of Figures viii
1 Introduction 1
1.1 Background . . . 1
1.1.1 Motivation . . . 1
1.1.2 Generalized Linear Mixed Models . . . 2
1.1.3 EM Algorithm . . . 6
1.2 Literature Review . . . 9
2 Seminonparametric Density 14 2.1 Introduction . . . 14
2.2 SNP Models . . . 15
2.3 Reparameterization . . . 16
2.3.1 Motivation . . . 16
2.3.2 Representation of SNP Densities . . . 18
2.4 Random Sampling from a SNP Density . . . 25
2.4.1 Acceptance–Rejection Method . . . 25
2.4.2 Sampling from a SNP Density . . . 30
3 Monte Carlo EM Algorithm 35 3.1 Introduction . . . 35
3.2 Monte Carlo EM Algorithms . . . 36
3.2.1 Motivation . . . 36
3.2.2 Metropolis–Hastings Algorithm . . . 38
3.2.3 Rejection Sampling Scheme . . . 39
3.3 Monte Carlo Error . . . 40
3.4 Standard Errors of the MLEs . . . 45
4 Semiparametric Generalized Linear Mixed Models 50
4.1 Model Specification . . . 50
4.2 “Double” Rejection Sampling . . . 53
4.3 MCEM Algorithm . . . 54
4.4 Standard Errors . . . 58
4.5 ChoosingK . . . 62
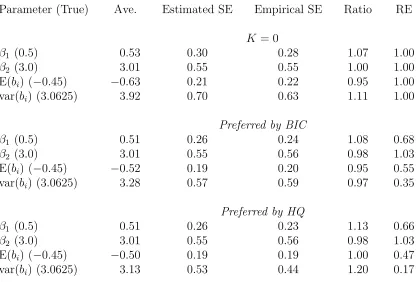
5 Simulation Results 65 5.1 Binary Response Data . . . 65
5.1.1 True Model and Assumptions . . . 65
5.1.2 Fitted Model and Assumptions . . . 66
5.1.3 Simulation Results . . . 68
5.2 Continuous Response Data . . . 75
6 Application 83 6.1 Six Cities Data . . . 83
6.2 Framingham Cholesterol Data . . . 87
7 Discussion 93
List of Tables
5.1 Simulation results for 100 binary data sets: mixture scenario . . . 71
5.2 Simulation results for 100 binary data sets: normal scenario . . . 72
5.3 Simulation results for 100 continuous data sets: mixture scenario . . . 78
5.4 Simulation results for 100 continuous data sets: normal scenario . . . 79
6.1 Results for the Six Cities study . . . 85
List of Figures
2.1 SNP densities with different estimates of coefficients in polynomial . . . 19 2.2 SNP density function with ψ = (0.58,1.56), µ=−0.11 andσ2 = 1.58. . . . 26 2.3 SNP density function with ψ = (−0.66,−1.21), µ=−0.01 andσ2 = 1.61. . 27 2.4 SNP density function with ψ = (0.30,1.57), µ=−0.2 and σ2 = 2.33. . . 28 2.5 SNP density function with ψ = (−0.36,−1.20), µ=−0.12 andσ2 = 2.68. . 29 2.6 Histogram of a random sample generated from a SNP density . . . 34
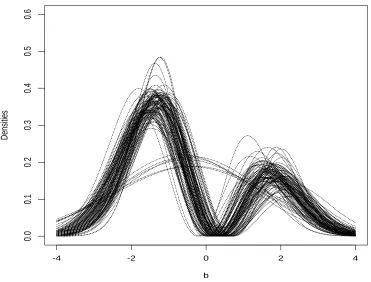
5.1 Averages of estimated densities for 100 binary data sets: mixture scenario. 73 5.2 100 estimated densities chosen by HQ for binary data sets: mixture scenario. 74 5.3 Averages of estimated densities for 100 continuous data sets: mixture scenario. 80 5.4 100 estimated densities chosen by HQ for continuous data sets: mixture
scenario. . . 81 5.5 15 estimated densities where K >0 was chosen by AIC for continuous data
sets: normal scenario. . . 82
6.1 Estimated random effects densities for fits to the Six Cities data. . . 86 6.2 Longitudinal cholesterol levels for five randomly chosen subjects. . . 90 6.3 Histogram of individual least squares intercept estimates in the cholesterol
Chapter 1
Introduction
1.1
Background
1.1.1
Motivation
A popular way to model correlated binary, count, or other data is by using generalized linear
mixed models, which accommodate correlation through incorporation of random effects. A
standard assumption is that the random effects are normally distributed; however this may
be unrealistic to represent the variation in the data.
In this thesis, we consider generalized linear mixed models where the random effects
are assumed only to have a “smooth” density. To fit this more flexible model, we propose
a Monte Carlo expectation–maximization (EM) algorithm that is straightforward to
im-plement. We also propose a strategy to choose the degree of flexibility required. In the
1.1.2
Generalized Linear Mixed Models
Generalized linear models (Nelder and Wedderburn 1972; McCullagh and Nelder 1989)
have been shown to unify the approach to regression for a wide variety of discrete and
continuous data, such as binary, count, and other data. They retain the linearity through
the incorporation of link functions.
Suppose data yi given xi, i = 1, . . . , m, are independent and arise from an exponential dispersion family with the following probability density function (pdf) or probability mass
function (pmf),
f(yi;θi, φ) = exp
½
yiθi−d(θi)
a(φ) +c(yi;φ)
¾
, (1.1)
where φ is a dispersion parameter whose value may be known; d(·), a(·) and c(·;·) are known functions. A generalized linear model assumes that µi = E(yi) =d0(θi), is related to the covariates xi through a link functiong(·), and the linear predictor ηi is given by
ηi =xTi β =g(µi),
has probability mass function
f(yi;πi) =πiyi(1−πi)1−yi = exp
½
yilog
µ
πi
1−πi
¶
+ log(1−πi)
¾
.
Therefore, θi = log{πi/(1−πi)}, µi =πi, and the logit link function is the canonical link, since
ηi =g(µi) = log
µ
πi
1−πi
¶
=θi.
A list of canonical link functions for some common univariate distributions in the
exponen-tial family can be found in Section 2.2 of McCullagh and Nelder (1989).
One natural principle for fitting generalized linear models is maximum likelihood
es-timation. Some standard numerical evaluation techniques are available to maximize the
log–likelihood function, such as the Newton–Raphson and Fisher scoring methods. It turns
out that the Fisher scoring method for generalized linear models can be implemented by
iteratively reweighted least squares (McCullagh and Nelder, 1989).
We usually use generalized linear models to analyze a wide variety of responses that
are assumed to be independent. However, the response data collected in some biomedical
studies might be correlated. For example, in a longitudinal study, repeated measures for
one subject are collected over time and hence are correlated. In a genetic study, data
collected among members of the same family are correlated since the family members share
a similar genetic factor. Linear mixed models (Laird and Ware, 1982), where random
effects are used to model the correlation in data, have become a popular framework for
levels of variability: random variation among measurements within a given unit and random
variation among units. Under the assumptions of normality and independence for these two
levels of random variation, the normal theory estimation of variance components can be
developed. Two important methods, maximum likelihood (ML) and restricted maximum
likelihood (REML) estimation, are described by Davidian and Giltinan (1995) in Section
3.3.
The class of generalized linear mixed models, GLMMs, (Schall 1991; Zeger and Karim
1991), which subsumes certain linear mixed models, extends the strategy of incorporation of
random effects to the generalized linear models. It is a popular way to represent correlated
binary, count or other data arising in clinical trials and epidemiological studies of cancer
and other diseases.
Let yij denote the jth response for the ith individual, i = 1, . . . , m and j = 1, . . . , ni. For each i, conditional on random effects bi (q×1), the yij, j = 1, . . . , ni are assumed to be independent and follow a generalized linear model (McCullagh and Nelder, 1989) with
density
f(yij|bi;β, φ) = exp
½
yijθij −d(θij)
a(φ) +c(yij;φ)
¾
, (1.2)
where µij = E(yij|bi) = d0(θij); φ is a dispersion parameter whose value may be known;
d(·),a(·) andc(·; ·) are known functions; and, for link functiong(·), the linear predictor
xij and sij for the fixed and random effects, respectively.
If we assume that the random effects bi have a parametric density f(bi;δ) which de-pends on parameters δ for each i, the specification of the generalized linear mixed model is completed, and the marginal likelihood for ζ can be written as
L(ζ;y) =
Z
f(y|b;β, φ)f(b;δ)db, (1.3)
where ζ is made up ofβ, φ and δ;
f(y|b;β, φ) =
m Y
i=1
f(yi|bi;β, φ),
f(yi|bi;β, φ) =
ni
Y
j=1
f(yij|bi;β, φ), (1.4)
and
f(b;δ) =
m Y
i=1
f(bi;δ);
1.1.3
EM Algorithm
The Expectation–Maximization (EM) algorithm was popularized by Dempster, Laird and
Rubin (1977). It is a clever way to compute complicated maximum likelihood estimation
from incomplete data such as missing, censored or truncated data. The name of EM
algorithm implies that it consists of an iterative computation of an expectation step followed
by a maximization step.
Let (x, y) be the “complete” data with the density function f(x, y;θ); x are missing data, y are observed data. The marginal likelihood function of θ given observed data y is given by
L(θ;y) = f(y;θ) =
Z
f(x, y;θ)dx. (1.5)
However, it is usually difficult to obtain a closed form for (1.5) for many applications. In
some cases, the EM algorithm can still obtain the MLE ofθmaximizingL(θ;y) numerically without having to do the integration in (1.5). Note that f(x, y;θ) =f(x|y;θ)f(y;θ). Thus we can write
logf(y;θ) = logf(x, y;θ)−logf(x|y;θ).
Now, suppose θ(r) is the value of θ at the rth iteration. Taking conditional expectations given y for both sides, evaluated at θ(r) yields
Let
Q(θ|θ(r)) = Eθ(r){logf(x, y;θ)|y},
and
H(θ|θ(r)) = Eθ(r){logf(x|y;θ)|y}.
The EM algorithm takes the form of an iterative procedure that, given therth iterateθ(r), we calculate Q(θ|θ(r)) in the expectation step and maximize Q(θ|θ(r)) with respect to θ in the maximization step to obtain θ(r+1). Each iteration will increase the log–likelihood. To show this, we consider the difference
logL(θ(r+1);y)−logL(θ(r);y)
= Q(θ(r+1)|θ(r))−Q(θ(r)|θ(r))− {H(θ(r+1)|θ(r))−H(θ(r)|θ(r))}.
Asθ(r+1) maximizesQ(θ|θ(r)) with respect toθ at the maximization step givenθ(r), it must be that
In addition, we have
H(θ(r+1)|θ(r))−H(θ(r)|θ(r))
= Eθ(r) ©
logf(x|y;θ(r+1))|yª−Eθ(r) ©
logf(x|y;θ(r))|yª
= Z ©logf(x|y;θ(r+1))ªf(x|y;θ(r))dx−Z ©logf(x|y;θ(r))ªf(x|y;θ(r))dx
=
Z ½
log f(x|y;θ (r+1))
f(x|y;θ(r))
¾
f(x|y;θ(r))dx.
Note that by Jensen’s inequality (Shorack, 2000, Sec. 3.4), since log(·) is a concave function,
we have
Z ½
log f(x|y;θ (r+1))
f(x|y;θ(r))
¾
f(x|y;θ(r))dx
≤ log
½Z
f(x|y;θ(r+1))
f(x|y;θ(r)) f(x|y;θ (r))dx
¾
= log
½Z
f(x|y;θ(r+1))dx
¾
= 0.
Thus, putting everything together, we have shown that
logL(θ(r+1);y)−logL(θ(r);y)≥0.
Under some regularity conditions, Dempster, Laird and Rubin (1977) showed that the
calculate and maximize. This is the case for a large class of problems, in particular, if the
underlying “complete” data come from an exponential family. For example, the application
of EM algorithm for usual linear mixed model was described by Laird and Ware (1982) and
Davidian and Giltinan (1995, Sec. 3.4). However, it is not always the case that we can find
a closed form for Q(θ|θ(r)), particularly for generalized linear mixed models. The Monte Carlo EM (MCEM) algorithm was developed by using a Monte Carlo approximation in the
E–step when the required integration may not be carried out analytically. More details on
the MCEM algorithm are in Chapter 3.
1.2
Literature Review
In contrast to generalized linear models and general linear mixed models, the estimation of
fixed effects β, dispersion parameter φ, and parameters specifying the distribution of the random effects in generalized linear mixed models is more complicated since the random
effects enter the models nonlinearly. The marginal likelihood, which requires the integration
over the distribution of random effects as in (1.3), may not have a closed form even for
normal random effects. Consequently, much work has focused on approximate techniques
that try to avoid the difficulty of integration.
Schall (1991) used the first order expansion of the link function g(·) applied to the data at the conditional mean µ and obtained the working vector (McCullagh and Nelder, 1989). This allows the model to be reduced to a linear mixed model by using the working
flexible random effects and just requires one to specify the variance function of the random
effects. However, this approximation based on the first order expansion may be very poor,
especially for binary responses.
Breslow and Clayton (1993) applied penalized quasi–likelihood (PQL) and marginal
quasi–likelihood (MQL) methods for the generalized linear mixed models. The key
as-sumption of using PQL is that the random effects are assumed to arise from a multinormal
distribution. These authors used Laplace’s method for the normal integral approximation
(Barndorff–Nielsen and Cox, 1989) and derived the score equations for the mean parameters
by using several ad hoc adjustments and approximations. For marginal quasi–likelihood, they derived the marginal models by using the first order approximation to the hierarchical
model. These methods may not be accurate because of the approximations, even though
they are adequate to provide starting values for use with other, more exact procedures.
Breslow and Lin (1995) and Lin and Breslow (1996) investigated the bias of these kinds of
estimators and provided bias–correction methods.
Alternatively, fully Bayesian analysis implemented via Markov chain Monte Carlo
tech-niques and expectation maximization algorithms was proposed by several authors. An
attractive feature of these methods is that they allow assessment the uncertainty in the
estimated random effects and functions of model parameters.
Zeger and Karim (1991) proposed an algorithm based on the Bayesian framework by
using a Gibbs sampling approach (Gelfand and Smith, 1990) to get the sample points from
Some authors proposed Monte Carlo EM algorithms for generalized linear mixed
mod-els. Expectation maximization algorithms (Dempster, Laird and Rubin, 1977) are usually
used to avoid difficult integration in complicated problems, provided that the conditional
expectation at the E–step and maximization at the M–step are easy to calculate. However,
we may not have a closed form for the conditional expectation of the log–likelihood at the
E–step for the generalized linear mixed models. Consequently, Monte Carlo approximation
at the E–step leads to a Monte Carlo EM algorithm.
McCulloch (1997) proposed a Monte Carlo EM algorithm for generalized linear mixed
models by using Metropolis–Hastings algorithm (Tanner, 1993) to produce random draws
from the conditional distribution of random effects given the observed data. The advantage
of using Metropolis–Hastings algorithm is that the calculation of acceptance probability
only depends on the specification of the conditional distribution of yi|bi; namely, the form of (1.4).
Booth and Hobert (1999) proposed another Monte Carlo EM algorithm by using a
rejection sampling scheme to construct a Monte Carlo approximation at the E–step.
Com-pared to the MCEM algorithm (McCulloch, 1997), the random draws by using a rejection
sampling method are independent and identically distributed. This has the advantage that
one can assess the Monte Carlo error at each iteration by using standard central limit
theory combined with the first–order Taylor series. This suggests a rule for automatically
increasing the Monte Carlo sample size after iterations in which the change of the
parame-ter values is swamped by Monte Carlo error. This generally saves considerable computing
However, the implementation of these algorithms (Breslow and Clayton, 1993; Zeger and
Karim, 1991; McCulloch, 1997; and Booth and Hobert, 1999) requires the assumption that
the random effects have distribution belonging to some parametric family, almost always the
normal. This implies symmetry and unimodality of the random effects distribution. But,
this may be unrealistic or too restrictive to represent the real data. Moreover, prediction of
individual unit effects may be compromised because of the misspecification of the random
effects distribution, raising concern over the validity of inferences both on fixed and random
effects if it is violated. Allowing the random effects distribution to have more complex
features than the symmetric, unimodal normal density may provide insight into underlying
heterogeneity of the population of units and even suggest failure to include important
covariates in the model.
Accordingly, considerable interest has focused on approaches that allow the parametric
assumption to be relaxed in mixed models (Davidian and Gallant, 1993; Madger and Zeger,
1996; Verbeke and Lesaffre, 1996; Kleinman and Ibrahim, 1998; Aitken, 1999; Jiang, 1999;
Tao et al., 1999; Zhang and Davidian, 2001). Many of these approaches assume only that the random effects distribution has a “smooth” density and represent the density in
different ways. In particular, for a general nonlinear mixed model (NLMM), Davidian and
Gallant (1992, 1993) assumed that the random effects have a “seminonparametric” (SNP)
density in a “smooth” class given by Gallant and Nychka (1987), which includes normal
distribution as a special case. Numerical integration was used to compute the likelihood.
Zhang and Davidian (2001) proposed use of the “seminonparametric” (SNP) representation
likelihood to be expressed in a closed form, facilitating straightforward implementation.
They showed that this approach yields attractive performance in capturing features of the
true random effects distribution and has potential for substantial gains in efficiency over
normal–based methods.
In this dissertation, we apply this technique to the more general class of GLMMs.
Although it is no longer possible to write the likelihood in a closed form, the fact that an
efficient algorithm is available for sampling from a SNP density allows an extension of the
Monte Carlo EM algorithm of Booth and Hobert (1999) to the case of a “smooth” but
unspecified random effects density involving no much greater computational burden than
when a parametric family is specified. In Chapter 2, we introduce and present the form of
SNP density, describe an algorithm to generate a random sample from a SNP density by
using acceptance–rejection methods. More details about Monte Carlo EM algorithm can be
found in Chapter 3. The semiparametric GLMM and the strategy to choose the degree of
flexibility required for the SNP density are described in Chapter 4. We present simulations
demonstrating performance of the approach and illustrate the methods by application to
Chapter 2
Seminonparametric Density
2.1
Introduction
The term “seminonparametric” or SNP was used by Gallant and Nychka (1987), to suggest
that it lies halfway between fully parametric and completely nonparametric specifications.
Gallant and Nychka (1987) showed that the SNP method, which is based on a truncated
version of the infinite Hermite series expansion, may be used as a general–purpose
approx-imation to densities satisfying certain smoothness restrictions, including differentiability
conditions, such that they may not exhibit unusual behavior such as kinks, jumps, or
os-cillation. However, they may be skewed, multi–model, fat– or thin–tailed relative to the
normal distribution, and also contain the normal as a special case. A full mathematical
description of “smooth” densities was given by Gallant and Nychka (1987). Thus, the
densities under certain smoothness restriction allow for the possibility of a wide range of
situations.
We give a detailed description of SNP parameterization in Section 2.3. An algorithm
to generate a random sample from a SNP density is described in Section 2.4.
2.2
SNP Models
Following Davidian and Gallant (1993) and Zhang and Davidian (2001), we propose to
represent the SNP density in the semiparametric generalized linear mixed model (SGLMM)
by the truncated version of the infinite Hermite series expansion, which we now describe.
More details in SGLMM can be found in Chapter 4.
Suppose Z is aq–variate random vector with density proportional to a truncated Her-mite expansion so that Z has density
hK(z)∝PK2(z)ϕq(z) (2.1)
for some fixed value of K, where PK(z) is a multivariate polynomial of orderK, andϕq(·) is the density function of the standard q–variate normal distribution with mean 0 and variance–covariance matrix Iq. Thus, for example, with z = (z1, z2)T, q= 2, and K = 2,
The proportionality constant is given by
1
R
P2
K(s)ϕq(s)ds
, (2.3)
which makes hK(z) integrate to 1. However, the coefficients in PK(z) can only be deter-mined to within a scalar multiple. To achieve a unique representation, it is standard to
put the constant term of the polynomial PK(z) to one; namely, a00 = 1 in the example (Davidian and Giltinan, 1995, Sec. 7.2). For convenience, we call
hK(z) = P 2
K(z)ϕq(z) R
P2
K(s)ϕq(s)ds
(2.4)
the standardq–variate SNP density function with degreeK. If K = 0,hK(z) is reduced to a standard q–variate normal distribution; when K > 0, hK(z) is a normal density whose shape is modified by the squared polynomial. The shape modification achieved is rich
enough to approximate a wide range of behavior, even forK = 1 or 2. We will discuss the choice of K in Section 4.5.
2.3
Reparameterization
2.3.1
Motivation
We have found that, when using the SNP representation as given above, numerical
K = 2 and q= 1, the standard univariate SNP densityh2(z) has the form of
h2(z) = (1 +a1z+a2z 2)2
C(a) ϕ1(z), (2.5)
where the proportionality constant C(a) = E(1 +a1U +a2U2)2, U ∼N(0,1), so that
C(a) = 1 +a21+ 3a22+ 2a2.
If max(a1, a2) is sufficiently large (≥30) and a2 ≥a1 without loss of generality, then
h2(z) = (1/a2 + (a1/a2)z+z 2)2 1/a2
2+ (a1/a2)2+ 3 + 2/a2
ϕ1(z)
≈ {(a1/a2)z+z2}2
(a1/a2)2+ 3 ϕ1(z), (2.6)
since 1/a2, 2/a2 and 1/a22 may be negligible. From (2.6), h2(z) does not change too much as long as a1 is proportional to a2. This leads to practical identifiability problems in that
a1 and a2 can not be identified separately. Actually, h2(z) might be a special SNP density function and has the form of
h2(z) = (1 +az) 2
C(a) z 2ϕ
1(z), (2.7)
which does not belong to the class defined by (2.5).
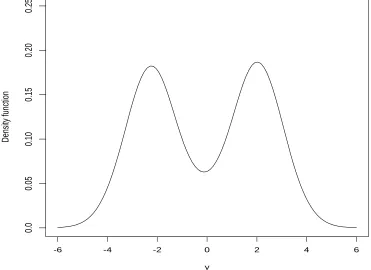
Figure 2.1, the true density is a mixture of normal distributions with the form 0.3n(y;−4,1)+ 0.7n(y; 3,1), where n(y;m, v) is the normal density with mean m and variancev. We try to use a general SNP density f2(y;µ, σ2) for a fixed value K = 2 to approximate the true density, which has the form of
f2(y;µ, σ2) = (1 +a1z+a2z2)2n(y;µ, σ2)/C(a),
where z = (y−µ)/σ, C(a) = 1 +a2
1+ 3a22+ 2a2. More description of general SNP density is given at the end of this section.
Figure 2.1 shows that three possible SNP densities with different estimates of a1, a2
and the same estimates of µ = −0.158, σ2 = 2.52 might be good. Actually, the density functionf2(y;µ, σ2) does not change too much and they are visually identical for the pairs (a1, a2) such that max(a1, a2)>30 anda2/a1 = 2.19. This suggests that the estimation of polynomial coefficients a1, a2 using this representation is very unstable.
2.3.2
Representation of SNP Densities
In order to circumvent the difficulty of numerical instability, we propose a
reparameteriza-tion of the coefficients in PK(z), which is an alternative way to provide a unique represen-tation and contains the special case SNP density given in (2.7). Let
PK(z) =
K X
|α|=0
y
Density function
-6 -4 -2 0 2 4 6
0.0
0.05
0.10
0.15
0.20
0.25
0.30
true
a=(2.69, 6.33) a=(10.65, 23.33) a=(85.2, 186.6)
where
α = (α1, α2, . . . , αq)T
is a multi–index (vector with nonnegative integer elements), and
|α|=
q X
i=1
αi,
zα =
q Y
i=1
zαi
i .
If we take the proportionality constant in (2.3) equal to 1, then hK(z) will be unique. It is equivalent to require that
E[PK2(U)] = 1, (2.8)
where U ∼N(0, Iq).
To have a convenient way to traverse the set {α : 0 ≤ |α| ≤ K}, let the J elements of {α : 0 ≤ |α| ≤ K} be ordered in some arbitrary way and denote that aα = pj, Uα = V
j,
j = 1, . . . , J. Then
PK(U) =
J X
j=1
pjVj =pTV,
where p = (p1, . . . , pJ)T and V = (V
1, . . . , VJ)T. Thus, for example, with q = 2, so that
U = (U1, U2)T, and K = 2,
and
V = (1, U1, U2, U12, U22, U1U2)T,
corresponding to (2.2). Therefore,
E[PK2(U)] = E(pTV VTp) =pT{E(V VT)}p=pTAp, (2.9)
where
A= E(V VT),
and is very straightforward to compute since every element is the expectation of the product
of powers of independent standard normal random variables. It is well known that A is a positive definite matrix. Thus it has a decomposition
A=BTB, (2.10)
where B is an upper triangle matrix. Therefore, substituting (2.10) and (2.9) into (2.8), we obtain
(Bp)TBp= 1,
i.e.,
where c=Bp= (c1, . . . , cJ)T. Thus, we can use the reparameterization
c1 = cos(ψ1)
c2 = sin(ψ1) cos(ψ2) ..
.
cj = sin(ψ1) sin(ψ2)· · ·cos(ψj) ..
.
cJ−1 = sin(ψ1) sin(ψ2)· · ·cos(ψJ−1)
cJ = sin(ψ1) sin(ψ2)· · ·sin(ψJ−1),
(2.11)
where ψj ∈(−π/2, π/2] for j = 1, . . . , J −1. Thus, with ψ = (ψ1, . . . , ψJ−1)T,
p=B−1c(ψ), (2.12)
where c(ψ) is a function of ψ satisfying (2.11).
The advantage of using this reparameterization is that it includes (2.7) as a special case
and has broad representation. Also, it will be more stable to estimate the parameters ψ
instead of p.
For example, with K = 2 andq= 1, let p= (p1, p2, p3)T and V = (1, U, U2)T. Then
Thus
A= E(V VT) = E
1 U U2
U U2 U3
U2 U3 U4
=
1 0 1
0 1 0
1 0 3
, B =
1 0 1
0 1 0
0 0 √2
,
B−1 =
1 0 −1/√2
0 1 0
0 0 1/√2
, and
c(ψ) =
cosψ1
sinψ1cosψ2
sinψ1sinψ2
.
Therefore, the coefficients in PK(z) are given by
p=B−1c(ψ) =
cosψ1−sinψ1sinψ2/√2 sinψ1cosψ2
sinψ1sinψ2/√2
.
p3 =√5/5. Thus the SNP density function has the special form of
h2(z) = ( √
10
5 +
√ 5 5 z)
2z2ϕ 1(z).
Ifψ1 =ψ2 = 0, thenh2(z) = ϕ1(z) will be a standard normal distribution. We thus propose to represent the density of Z as
hK(z;ψ) = PK2(z;ψ)ϕq(z), (2.13)
where the notation PK(z;ψ) emphasizes that the polynomial is parameterized in terms of
ψ.
Now, suppose Y = RZ+γ, where R is a (q×q) upper triangular matrix and γ is a
q–vector. Then the density function of Y is straightforward to compute and is given by
fK(y;δ) = PK2(z;ψ)nq(y;γ,Σ), (2.14)
where z = R−1(y−γ), Σ =RRT and n
q(y;γ,Σ) is a q–variate multinormal density with
mean γ and variance–covariance matrix Σ. The parameters δ are made up of ψ, γ and R. This is the general form of SNP density function we will use.
The shape of general SNP density function fK(y;δ) is rich enough to approximate a wide range of behaviors. Densities with this representation can be skewed, multi–modal,
multi–modal, symmetric as well as very skewed.
2.4
Random Sampling from a SNP Density
2.4.1
Acceptance–Rejection Method
Gallant and Tauchen (1992) proposed an algorithm to generate a random sample from a
SNP density. We apply this algorithm for our representation of SNP densities. We first
describe acceptance–rejection methods (Kennedy and Gentle, 1980) for sampling from an
arbitrary density h(z). This depends on finding a positive, integrable function d(z) that dominates h(z), i.e.,
0≤h(z)≤d(z), for any z.
In this case, d(z) is called an upper envelope for h(z) or a majorizing function. Derive a density g(z) from d(z) by normalizing
g(z) = R d(z)
d(s)ds.
Usingd(z) and g(z), a sample z fromh(z) is generated as follows.
1. Generate the pair (u, v) independently, u∼U(0,1), v ∼g(v).
2. If u≤h(v)/d(v) then accept z =v; otherwise, go to 1 and repeat until one sample z
y
Density function
-6 -4 -2 0 2 4 6
0.0
0.05
0.10
0.15
0.20
0.25
y
Density function
-6 -4 -2 0 2 4 6
0.0
0.05
0.10
0.15
0.20
0.25
0.30
y
Density function
-6 -4 -2 0 2 4 6
0.0
0.05
0.10
0.15
0.20
y
Density function
-6 -4 -2 0 2 4 6
0.0
0.05
0.10
0.15
0.20
The algorithm can be proved by the following arguments:
Pr(z ≤t) = Pr[{(u, v) :v ≤t}|{(u, v) :u≤h(v)/d(v)}]
= Pr[(u, v) :v ≤t, u≤h(v)/d(v)] Pr[(u, v) :u≤h(v)/d(v)]
=
R v≤t
Rh(v)/d(v)
0 g(v)dudv
R v≤∞
Rh(v)/d(v)
0 g(v)dudv =
R
v≤tg(v)h(v)/d(v)dv R
v≤∞g(v)h(v)/d(v)dv
=
R
v≤th(v)dv R
v≤∞h(v)dv
=
Z
v≤t
h(v)dv.
Thus,z generated by the above rejection method is a sample fromh(z).
2.4.2
Sampling from a SNP Density
For our problem, we need to find an upper envelopedK(z) for SNP densityhK(z). We have
hK(z) = PK2(z;ψ)ϕq(z),
and
PK(z;ψ) =
K X
|α|=0
Note that the coefficient aα inPK(z;ψ) is a function ofψ, for {α: 0≤ |α| ≤K}, which is defined in (2.12). Since
K X
|α|=0
aαzα ≤
K X
|α|=0
|aα||z|α,
where |z|denotes the vector z with each element replaced by its absolute value,
dK(z) =
K X
|α|=0
|aα||z|α
2
ϕq(z)
is an upper envelope for hK(z), and the densitygK(z) is given by
gK(z) = R dK(z)
dK(s)ds.
To obtain the density gK(z), note that
dK(z) =
K X
|α|=0
K X
|γ|=0
|aα||aγ||z|α+γϕq(z)
=
K X
|α|=0
K X
|γ|=0
|aα||aγ|
(√2π)q ( q
Y
i=1
|zi|αi+γie−zi2/2
)
=
K X
|α|=0
K X
|γ|=0
|aα||aγ|
(√2π)q ( q
Y
i=1
Γ[(αi+γi+ 1)/2]2(αi+γi+1)/2−1
)
( q Y
i=1
χ(|zi|;αi +γi+ 1)
is the weighted sum ofChidensity functions (Monahan, 1987), where theChidensity with
ν degrees of freedom is given by
χ(s;ν) = 2 1−ν/2 Γ(ν/2)s
ν−1e−s2/2,
for s >0. Thus we can obtain the density
gK(z) =
K X
|α|=0
K X
|γ|=0
ωαγ
q Y
i=1
χ(|zi|;αi+γi+ 1),
where
ωαγ = |aα||aγ|
i=1Γ[(αi+γi+ 1)/2]2(αi+γi+1)/2−1
PK
|α|=0
PK
|γ|=0|aα||aγ| Qq
i=1Γ[(αi+γi+ 1)/2]2(αi+γi+1)/2−1
.
In order to sample fromgK(z), we need to obtain a sample (α, γ) from the setF(α, γ) = {(α, γ) : 0 ≤ |α| ≤ K,0 ≤ |γ| ≤ K}. This can be done as follows. Let the elements of
F(α, γ) be ordered in an arbitrary way so that it can be indexed by the sequence (α, γ)j, wherej = 0,1, . . . , J. Letωj =ωαγ where (α, γ) = (α, γ)j. Generateu∼U(0,1). Find the largestL such thatPLj=0ωj ≤u. Then let (α, γ) = (α, γ)L. For this given (α, γ), generate
zi from χ(zi;αi+γi+ 1) for all i = 1, . . . , q. Then change the sign of zi with probability 1/2. That is, change the sign of zi if u1 ≤1/2; otherwise, do not change it, where u1 is a random sample from the uniform (0, 1) distribution. Thenz = (z1, z2, . . . , zq)T is a sample
2. For the given (α, γ), sample z from gK(z).
3. GenerateufromU(0,1) independently. Ifu≤hK(z)/bK(z), then acceptz; otherwise, go to 1 and repeat until one sample point is obtained.
If we wish to obtain a sample y from (2.14), we can generate a sample z from hK(z) first. Then y=Rz+γ is a random sample fromfK(y).
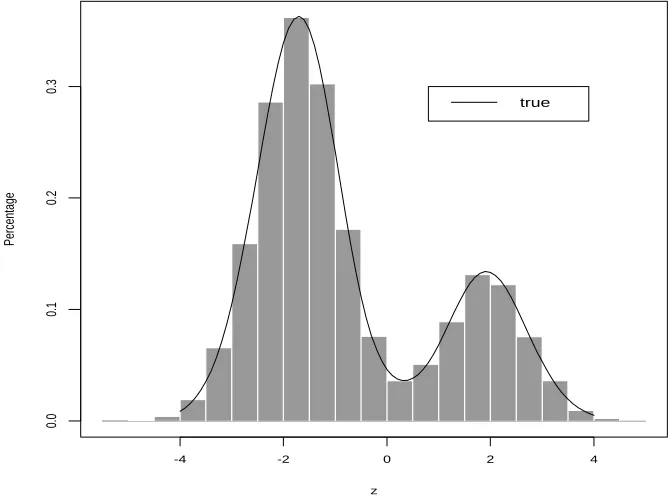
Here we show an example to illustrate the performance of this algorithm. For K = 2 and q = 1,
h2(z) = P22(z;ψ)ϕ1(z),
where P2(z;ψ) = a0+a1z+a2z2, ϕ
1(z) is the standard normal distribution density. Let
ψ = (−0.7,−1.2). Then we can obtaina= (0.340270,−0.233437,0.424572) by using (2.12). For this example, the rejection algorithm above works efficiently and achieves an acceptance
rate of about 70%. We generated 15000 sample points from this SNP density. Figure 2.6
is the histogram of these 15000 sample points and the true density function. The shape
of histogram matches perfectly to the true SNP density, which shows that this algorithm
works very well and that the sample generated by the algorithm really arises from the true
-4 -2 0 2 4
0.0
0.1
0.2
0.3
z
Percentage
true
Chapter 3
Monte Carlo EM Algorithm
3.1
Introduction
If we are willing to assume the response of interest follows some distributional model, the
likelihood method is usually a good way to estimate the parameters which specify the
dis-tributions. However, the likelihood function is not easy to obtain for some complicated
problems like generalized linear mixed models even with normal random effects, which
involves the integration over the random effects. One way to avoid the difficulty of
integra-tion is to use the EM algorithm and treat the random effects as “missing” data. However
we have the same difficulty at the E–step in the generalized linear mixed model context,
because the E–step involves an intractable integral. Some methods were developed by
us-ing Monte Carlo approximation to the required integration at the E–step. The resultus-ing
3.2
Monte Carlo EM Algorithms
3.2.1
Motivation
In models such as the generalized linear mixed model, the likelihood is of the form
L(ζ;y) =
Z
f(y|b;β, φ)f(b;δ)db. (3.1)
To avoid the difficulty of integration, one clever way is to use the EM algorithm and treat
the random effects b as “missing” data, and y as “observed” data (e.g. Searle et al., 1992, Chap. 8). Then the “complete” data (y, b) have the joint density function f(y, b;ζ) which is the same as the integrand in (3.1). Given the rth iterate estimate ζ(r), at the (r+ 1)th iteration, the E–step involves the calculation of
Q(ζ|ζ(r)) = E{logf(y, b;ζ)|y;ζ(r)}=
Z
logf(y, b;ζ)f(b|y;ζ(r))db, (3.2)
where f(b|y;ζ(r)) is the conditional distribution of b given y. The M–step consists of maximizing Q(ζ|ζ(r)) with respect to ζ to yield the new update ζ(r+1). The process is iterated from a starting valueζ(0) to convergence; under regularity conditions, the value at convergence maximizes the likelihood function (3.1).
Obtaining a closed form expression for (3.2) is often not possible, as it requires
knowledge of the marginal likelihood whose direct calculation is to be avoided. In
or-der to circumvent this difficulty, much effort (Wei and Tanner, 1990; McCulloch, 1997;
Booth and Hobert, 1999) has been made to use a Monte Carlo approximation to the
re-quired integration at the E–step. Specifically, if it is possible to obtain a random sample
(b(1), b(2), . . . , b(L))T from f(b|y;ζ(r)), then (3.2) may be approximated by at the (r+ 1)th iteration
QL(ζ|ζ(r)) = 1
L
L X
l=1
logf(y, b(l);ζ), (3.3)
yielding a so–called Monte Carlo EM (MCEM) algorithm. By independence, to obtain a
sample from f(b|y;ζ(r)), one may sample from the conditional distribution of b
i given yi
evaluated at ζ(r),f(b
i|yi;ζ(r)), say, for eachi.
Incorporating the Monte Carlo approximation into the EM algorithm gives an MCEM
algorithm as follows.
1. Choose starting values ζ(0). Set r= 0.
2. At iteration (r+ 1), generate b(l) fromf(b|y;ζ(r)),l = 1, . . . , L.
3. Using the approximation (3.3), obtain ζ(r+1) by maximizingQ
L(ζ|ζ(r)).
4. If convergence is achieved, set ζ(r+1) to be the maximum likelihood estimate ζb; oth-erwise, set r=r+ 1 and return to 2.
To complete the MCEM algorithm, we need to know how to generate such random
algorithm (McCulloch, 1997) and rejection sampling scheme (Booth and Hobert, 1999).
3.2.2
Metropolis–Hastings Algorithm
McCulloch (1997) proposed using the Metropolis–Hastings algorithm (Tanner, 1993) to
pro-duce a Markov chain from the conditional distribution of bi|yi. To specify the Metropolis– Hastings algorithm, it is important to specify the candidate distribution and calculate the
acceptance function at each iteration. If we choose the marginal distribution of random
effect bi, f(bi;δ(r)), as the candidate distribution at the rth iteration, then the acceptance function takes a neat form. Suppose bi is the previous draw from the conditional density
f(bi|yi;ζ(r)) and we generate a new value b∗
i from the candidate distribution f(bi;δ(r)).
Then, we accept b∗i as a sample point from the conditional distribution with probability
A(bi, b∗i); otherwise, we retain bi, and A(bi, b∗i) is given by
A(bi, b∗i) = min
½
1,f(b
∗
i|yi;ζ(r))f(bi;δ(r))
f(bi|yi;ζ(r))f(b∗
i;δ(r)) ¾
= min
½
1,f(b
∗
i, yi;ζ(r))f(bi;δ(r))
f(bi, yi;ζ(r))f(b∗
i;δ(r)) ¾
= min
½
1,f(yi|b
∗
i;ζ(r))
f(yi|bi;ζ(r))
¾
= min
(
1,
Qni
j=1f(yij|b∗i;ζ(r)) Qni
j=1f(yij|bi;ζ(r)) )
.
2. Generate a random sample u ∼ U(0,1) independently and take the new value as
bnewi =b∗i if u≤A(bi, b∗i); otherwise, bnewi =bi, where bi is the previous draw in the Markov chain.
3.2.3
Rejection Sampling Scheme
Alternatively, Booth and Hobert (1999) proposed using a rejection sampling scheme (Geweke,
1996) to generate random samples from the conditional distributionf(bi|yi;ζ(r)). A random sample from f(bi|yi;ζ(r)) can be obtained as follows.
1. Generate a random sample b∗i from f(bi;δ(r)).
2. Sample u∼ U(0,1) independently. If u≤f(yi|b∗i;ζ(r))/τ
i, accept bi =b∗i; otherwise,
return 1 and repeat until a sample bi is obtained,
where τi = supbif(yi|bi;ζ(r)). Note that
Pr(bi ≤t) = Pr[{(bi∗, u) :b∗i ≤t}|{(bi∗, u) :u≤f(yi|b∗i;ζ(r))/τi}] = Pr[(b
∗
i, u) :b∗i ≤t, u≤f(yi|b∗i;ζ(r))/τi]
Pr[(b∗i, u) :u≤f(yi|b∗i;ζ(r))/τ
i]
=
R b∗i≤t
Rf(yi|b∗
i;ζ(r))/τi
0 f(b∗i;δ(r))dudb∗i R
b∗i≤∞
Rf(yi|b∗
i;ζ(r))/τi
0 f(b∗i;δ(r))dudb∗i
=
R
b∗i≤tf(yi|b∗i;ζ(r))f(b∗i;δ(r))db∗i R
b∗i≤∞f(yi|b∗i;ζ(r))f(b∗i;δ(r))db∗i
=
R
b∗i≤tf(yi, b∗i;ζ(r))db∗i
f(yi;ζ(r)) =
Z
Therefore,bi generated by the rejection sampling scheme is indeed a random sample from
f(bi|yi;ζ(r)).
3.3
Monte Carlo Error
Unlike the Metropolis–Hastings approach in which the random samples generated in the
Markov chain are dependent, the rejection sampling scheme produces independent and
identically distributed random samples that may be used to assess Monte Carlo error at
each iteration of the MCEM algorithm and hence suggest a rule for changing the sample
size L to enhance speed.
Suppose (b(1), b(2), . . . , b(L)) is a random sample generated from f(b|y;ζ(r)) using the rejection sampling scheme. Let
Q(1)(ζ|ζ(r)) = ∂
∂ζQ(ζ|ζ
(r)),
Q(2)(ζ|ζ(r)) = ∂ 2
∂ζ∂ζTQ(ζ|ζ
(r)),
and define Q(1)L (ζ|ζ(r)) and Q(2)
L (ζ|ζ(r)) similarly, where
Q(ζ|ζ(r)) = E{logf(y, b;ζ)|y;ζ(r)},
and
Q (ζ|ζ(r)) = 1
L X
Now, suppose we obtain ζ(r+1) and ζ∗(r+1) by maximizing QL(ζ|ζ(r)) and Q(ζ|ζ(r)) respec-tively, i.e.,
Q(1)L (ζ(r+1)|ζ(r)) = 0,
and
Q(1)(ζ∗(r+1)|ζ(r)) = 0.
Combining with first order Taylor series expansion, we have
0 = Q(1)L (ζ(r+1)|ζ(r))
≈ Q(1)L (ζ∗(r+1)|ζ(r)) +Q(2)L (ζ∗(r+1)|ζ(r))(ζ(r+1)−ζ∗(r+1)).
Thus,
(ζ(r+1)−ζ∗(r+1))≈ {−Q(2)L (ζ∗(r+1)|ζ(r))}−1Q(1)L (ζ∗(r+1)|ζ(r)),
and
√
L(ζ(r+1)−ζ∗(r+1))≈ {−Q(2)L (ζ∗(r+1)|ζ(r))}−1{√LQ(1)L (ζ∗(r+1)|ζ(r))}.
Since (b(1), b(2), . . . , b(L)) are i.i.d. from f(b|y;ζ(r)), by the weak law of large numbers (Lehmann, 1998, Sec. 2.1), we have
−Q(2)L (ζ∗(r+1)|ζ(r)) = −1
L
L X
l=1
∂2
∂ζ∂ζT logf(y, b
(l);ζ∗(r+1)) → E
½
− ∂2
∂ζ∂ζT logf(y, b;ζ
∗(r+1))|y;ζ(r)
¾
and
√
LQ(1)L (ζ∗(r+1)|ζ(r)) =√L
( 1 L L X l=1 ∂
∂ζ logf(y, b
(l);ζ∗(r+1))
)
.
By the multivariate central limit theorem (Lehmann, 1998, Sec. 5.4), √LQ(1)L (ζ∗(r+1)|ζ(r)) follows a multivariate normal distribution with mean
E ∂
∂ζ logf(y, b
(1);ζ∗(r+1)) = Q(1)(ζ∗(r+1)|ζ(r)) = 0,
and variance
var
½
∂
∂ζ logf(y, b
(1);ζ∗(r+1))
¾
= E
(·
∂
∂ζ logf(y, b
(1);ζ∗(r+1))
¸ ·
∂
∂ζ logf(y, b
(1);ζ∗(r+1))
¸T)
= E
(·
∂
∂ζ logf(y, b;ζ
∗(r+1))
¸ ·
∂
∂ζ logf(y, b;ζ
∗(r+1))
¸T
|y;ζ(r)
)
def
= B(ζ∗(r+1)|ζ(r)).
Thus, by Slutsky’s theorem (Lehmann, 1998, Sec. 5.1), asymptotically,
ζ(r+1) a∼N(ζ∗(r+1), 1 LΛ
(r+1)),
where Λ(r+1) in the Monte Carlo error for ζ(r+1) is given by
At the (r+ 1)th iteration, we can use Q(2)L (ζ(r+1)|ζ(r)) andB
L(ζ(r+1)|ζ(r)) as estimators for
Q(2)(ζ∗(r+1)|ζ(r)) and B(ζ∗(r+1)|ζ(r)), where
Q(2)L (ζ(r+1)|ζ(r)) = 1
L
L X
l=1
∂2
∂ζ∂ζT logf(y, b
(l);ζ(r+1)), (3.4)
and
BL(ζ(r+1)|ζ(r)) = 1
L L X l=1 ½ ∂
∂ζ logf(y, b
(l);ζ(r+1))
¾
½
∂
∂ζ logf(y, b
(l);ζ(r+1))
¾T
. (3.5)
A sandwich estimator for Λ(r+1)is obtained by substitutingQ(2)L (ζ(r+1)|ζ(r)) andBL(ζ(r+1)|ζ(r))
b
Λ(r+1) =
n
Q(2)L (ζ(r+1)|ζ(r))
o−1
BL(ζ(r+1)|ζ(r))
n
Q(2)L (ζ(r+1)|ζ(r))
o−1
.
With the normal approximation of Monte Carlo error at each iteration of the MCEM
algorithm, an approximate 100(1−α)% confidence ellipsoid forζ∗(r+1) can be constructed. Since
ζ(r+1) a∼N(ζ∗(r+1), 1 LΛb
(r+1)),
we have
½
1
LΛb
(r+1)
¾−1/2
and thus
(ζ(r+1)−ζ∗(r+1))T
½
1
LΛb
(r+1)
¾−1
(ζ(r+1)−ζ∗(r+1))∼χ2s,
where s is the number of parameters in ζ. Thus, a 100(1−α)% confidence ellipsoid for
ζ∗(r+1) is given by
(ζ∗(r+1)−ζ(r+1))T
½
1
LΛb
(r+1)
¾−1
(ζ∗(r+1)−ζ(r+1))≤χ2s,1−α.
Booth and Hobert (1999) advocated updating L as follows. If the previous value ζ(r) is inside of this confidence region, i.e.
(ζ(r)−ζ(r+1))T
½
1
LΛb
(r+1)
¾−1
(ζ(r)−ζ(r+1))≤χ2s,1−α,
they recommended increasing Lby the integer part ofL/k, where k is a positive constant; otherwise, retainL. The choice ofαandkneeds further investigation. They have advocated choosing α = 0.25 andk ∈ {3,4,5}.
Combining the above, the MCEM algorithm, incorporating a rejection sampling scheme,
is as follows.
1. Choose starting values ζ(0) and initial sample sizeL. Set r = 0.