Computational Modeling of Tensile Stress Effects on the Structure and Stability of Prototypical Covalent and Layered Materials
Full text
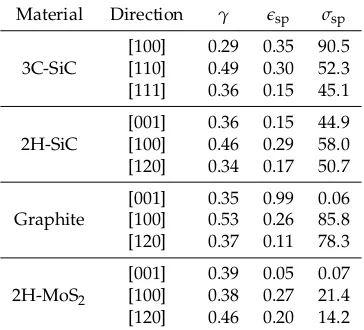
Figure


Related documents
It was decided that with the presence of such significant red flag signs that she should undergo advanced imaging, in this case an MRI, that revealed an underlying malignancy, which
In Afghanistan, this is a qualification through either the Institute of Health Sciences or the Community Midwifery Education programme.. Skilled
If one has a control group and a group treated with methyl prednisolone, and they are killed at the same time (in this instance on the 21st day) one finds that the tumors
When leaders complete Basic Leader Training at (name of council), they are asked to fill out an evaluation on the training. The immediate feedback new leaders give is
19% serve a county. Fourteen per cent of the centers provide service for adjoining states in addition to the states in which they are located; usually these adjoining states have
"A Food-Based Approach Introducing Orange- Fleshed Sweet Potatoes Increased Vitamin A Intake and Serum Retinol Concentrations in Young Children in Rural Mozambique."
Twenty-five percent of our respondents listed unilateral hearing loss as an indication for BAHA im- plantation, and only 17% routinely offered this treatment to children with
See also [14], [13] and the references therein for more details about the evolu- tion semigroups on half line and their connections with asymptotic behaviour of evolution families