INVESTIGATION
Serial Founder Effects During Range Expansion:
A Spatial Analog of Genetic Drift
Montgomery Slatkin*,1and Laurent Excoffier†,‡
*Department of Integrative Biology, University of California, Berkeley, California 94720-3140,†Computational and Molecular Population Genetics, Institute of Ecology and Evolution, University of Berne, 3012 Berne, Switzerland, and
‡Swiss Institute of Bioinformatics, 1015 Lausanne, Switzerland
ABSTRACTRange expansions cause a series of founder events. We show that, in a one-dimensional habitat, these founder events are the spatial analog of genetic drift in a randomly mating population. The spatial series of allele frequencies created by successive founder events is equivalent to the time series of allele frequencies in a population of effective size ke, the effective number of founders. We derive an expression forkein a discrete-population model that allows for local population growth and migration among established populations. If there is selection, the net effect is determined approximately by the product of the selection coefficients and the number of generations between successive founding events. We use the model of a single population to compute analytically several quantities for an allele present in the source population: (i) the probability that it survives the series of colonization events, (ii) the probability that it reaches a specified threshold frequency in the last population, and (iii) the mean and variance of the frequencies in each population. We show that the analytic theory provides a good approximation to simulation results. A consequence of our approximation is that the average heterozygosity of neutral alleles decreases by a factor of 1–1/(2ke) in each new population. Therefore, the population genetic consequences of surfing can be predicted approximately by the effective number of founders and the effective selection coefficients, even in the presence of migration among populations. We also show that our analytic results are applicable to a model of range expansion in a continuously distributed population.
R
ANGE expansion through a series of colonization events can produce geographic patterns in allele frequencies that are quite different from what is expected in equilibrium populations. One consequence of range expansion is the steady reduction of heterozygosity with increasing distance from the ancestral population (Austerlitz et al. 1997; DeGiorgio et al. 2011), a pattern well documented in human populations (Prugnolle et al. 2005; Ramachandranet al. 2005; Handley et al.2007; Liet al.2008; DeGiorgioet al.2009; Deshpande et al. 2009). Another consequence is that some alleles may reach a high frequency because of repeated founder events (Edmonds et al. 2004), a process called genetic surfing (Excoffier et al. 2009). Even deleterious alleles may reach a high frequency because of surfing (Klopfsteinet al.2006; Traviset al.2007; Excoffier and Ray 2008; Hallatschek and Nelson 2010; Hallatschek 2011). In addition to these simu-lation-based studies, the analytic theory of surfing in termsof reaction–diffusion equations has been developed (Vlad et al. 2004; Hallatschek and Nelson 2008; Hallatschek 2011). The serial-founder model has also been investigated by coalescent approaches (Austerlitzet al.1997; DeGiorgio et al.2011) and the theory has been used to date the time of the onset of human expansions from Africa (Liuet al.2006). In this article, we show that the effect of range expansion in a one-dimensional habitat is analogous to the effect of random mating in a single population. The spatial series of allele frequencies in a one-dimensional array of populations can be predicted from the standard theory of a single population in which the effective population size is set to an effective propagule size that depends on migration and population growth in each newly founded population, and the selection coefficients are set to effective selection coefficients that depend on the number of generations between successive colonization events. We use the theory of a single population to predict several quantities, including (i) the probability that an allele present in the initial population will persist through-out the range expansion, (ii) the probability that an allele will reach high frequency after the range expansion is complete, (iii) the average allele frequency in each population, and (iv) Copyright © 2012 by the Genetics Society of America
doi: 10.1534/genetics.112.139022
Manuscript received December 8, 2011; accepted for publication February 1, 2012 1Corresponding author: Department of Integrative Biology, VLSB 3060, University of
the rate of decrease in heterozygosity with increasing distance from the founding population. The analytic approximation also allows us to relate the discrete-population model to a model of range expansion in a continuously distributed population.
Our analytic approximation is not intended to replace simulations. In fact, even with relatively large effective pro-pagule sizes, there is considerable stochastic variability in allele frequency after a range expansion, making it difficult to predict what will happen to any one allele. Instead, the theory is intended as a guide to intuition because it shows how each parameter in a model of range expansion influences the intensity of founder effects.
We present our results in several parts: (i) we define an idealized model of range expansion that ignores some of the complexity we allow for later, (ii) we develop analytic theory of a Wright–Fisher model of a single population that is analogous to the idealized model of range expansion, (iii) we compare analytic results for the Wright–Fisher model to simulation results for the idealized model, (iv) we define a more realistic model of range expansion and show that it can be matched to the idealized model by redefining parameters, (v) we compare simulation results of the realistic model with the predictions of the analytic theory of the Wright–Fisher model, and (vi) we discuss the relationship between discrete-population models of range expansion and range expansion in a continuously distrib-uted population.
Idealized Model of Range Expansion
In our idealized model there are n+ 1 sites at which pop-ulations can be established. They are arranged on a line and numbered 0–n. Att= 0, site 0 is occupied by a diploid pop-ulation of effectively infinite size in which an allele A is present in frequency x0 in zygotes. Selection changes the frequency deterministically to x09 among adults. Then, k adults are drawn randomly to found a new population at site 1. The propagule at site 1 grows in one generation into a population of zygotes of effectively infinite size. Selection then modifies the frequencies in populations 0 and 1, and
finallyk adults are chosen randomly from population 1 to found population 2. This process continues for n–1 more generations, with selection affecting the frequency in each established population each generation. Afterngenerations, all nsites are occupied. Our concern is with the frequency trajectory, x¼ fx0 ;x1;. . .; xng, at time n given that Ahas
not been lost from the population. Note that if A is not neutral, thefinalx0will differ from the initial value because of selection acting for ngenerations.
Wright–Fisher Model of a Single Population
The idealized model of range expansion is similar to a model of random mating in a single population containing k in-dividuals. The time sequence of allele frequencies in the randomly mating population is preserved in the spatial
se-quence of frequencies in the model of range expansion. The only difference is that, if there is selection, then selection continues to modify the allele frequency after a population sends a propagule to found the next population.
Given the similarity of the two models, we can use the well-developed theory of drift and selection in single pop-ulations to predict what is seen after all poppop-ulations are colonized. We assume a Wright–Fisher model of a popula-tion of size k. The relativefitnesses of individuals with 0, 1, and 2 copies of A are 1, 1–s1, and 1–s2, respectively. We are concerned with the case in which A is deleterious or neutral (s2$s1$0). We follow the notation of Chap. 2.12 of Ewens (2004). At any time, the population is in a stateEi,
i¼0,. . ., 2k, withicopies ofApresent. The transition prob-ability fromEitoEjis
pij¼
2k j
x9jð12x9Þ2k2j; (1)
wherex¼i=ð2kÞand
x9¼ x½12s2x2s1ð12xÞ 12s2x222s1xð12xÞ:
(2)
LetpðijtÞdenote thet-generation transition probability. The probability thatAsurvives forngenerations, given that it is present inicopies initially, is
Sði;nÞ ¼12pðnÞi0 : (3)
For large n,S(i, n) approaches the probability of ultimate
fixation.
Given the initial number of copies ofA,i0, the Wright– Fisher model will generate a trajectory, i ¼ (i0, i1, ..., in), where it is the number of copies of A at time t. The
pro-bability of any trajectory given thatin.0 (i.e., thatA
sur-vives) is
Prðijin . 0Þ ¼
Qn21
t¼0pititþ1
Sði0;nÞ : (4)
We can use the Wright–Fisher model to calculate other quantities of interest. One is the probability thatAwill reach a specified number of copies,j, aftertgenerations:
Prðin $ jÞ ¼
X2k
i¼j
pðtÞi0i: (5)
And we can predict the decrease in heterozygosity as a function of t,
HðtÞ ¼
121 2k
t
Hð0Þ; (6)
The probability oficopies ofAat timet, given nonloss at timen, is
Prði;tjin .0Þ ¼p ðtÞ i0i
12pðni02tÞ
Sði0;nÞ ; (7)
from which the mean and variance of the number of copies ofAcan be computed,
Eði;tjin . 0Þ ¼X
2k
i¼1
i Prði;tjin . 0Þ; (8)
with a similar equation for the second moment ofi.
Comparison of the Idealized and Wright–Fisher Models
The Wright–Fisher model is analogous to our idealized model of range expansion. IfAis neutral,it is the number
of copies ofAin the propagule that founds populationt. The assumption that each population immediately grows to an effectively infinite size ensures that the frequency ofAwill remain the same in each population and hencext¼it=ð2kÞ.
The idealized model differs slightly from the Wright– Fisher model ifAis not neutral because selection will modify the frequency in populationtforn–tmore generations. This additional effect of selection makes no difference in the cal-culation of eitherSði0; nÞor Prðin $ jÞ because they do not
depend on frequencies in the intermediate populations. To predict the effect of selection on the average frequency in the intermediate populations, we first calculated EðxtÞ ¼Eðitjin.0Þ=ð2kÞand then deterministically changed
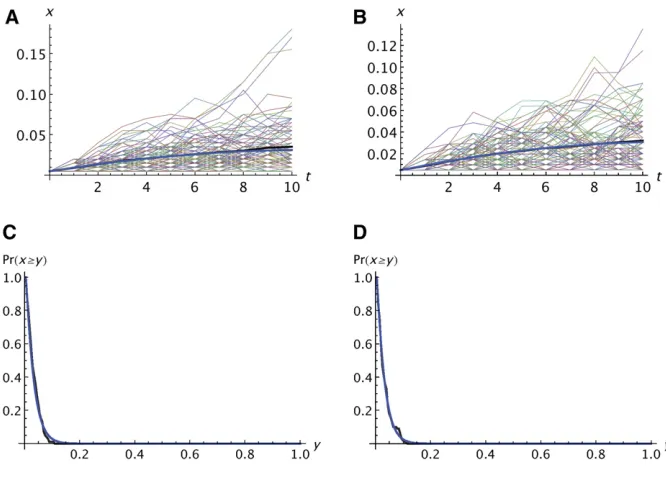
the frequency by applying Equation 2 forn–tgenerations. We simulated the idealized model to test the accuracy of the analytic approximation on the basis of the Wright–Fisher model. Typical results are shown in Figure 1. The fit of the average allele frequency in the simulations to the expectation calculated from the analytic theory is quite good for both neu-tral and deleterious alleles. There is considerable variation among replicates, however; most trajectories deviate sub-stantially from the average. Some trajectories are clinal with a roughly monotonic increase in frequency while others reach an intermediate maximum and then decrease. For Figure 1A, the predicted and observed survival probabilities are 0.159 and 0.158, and in Figure 1B, they are 0.158 and 0.147. The prob-ability that an allele reaches at least a given frequency is also predicted accurately by the analytic theory (Figure 1, C and D).
Realistic Model: Finite Population Size and Migration
To create a more realistic model, we assume each propagule grows in one generation to sizeN(.k) and remains at that size for T generations before generating a propagule that colonizes the next site. We also allow for migration: each established population, including population 0, receives immigrants at a ratemper generation from each neighbor-ing population. The migration among established
popula-tions continues until all sites are occupied and the process is stopped. We are concerned with weak migration only and ignore the effect of migration on population growth and population size.
These additional features make the resulting model intractable because it is no longer analogous to a Wright– Fisher model. However, the realistic model can be approxi-mated by the Wright–Fisher model if the parameters of that model are defined in a way that equalizes the mean and variance of the change in allele frequencies between succes-sive colonization events. In Appendix A, we show that the variance in the change in allele frequency in a realistic model is the same as that in the Wright–Fisher model ifk is replaced by
ke¼
1
aT= kþ ð12aTÞ=Nð1 2aÞ; (9)
where a¼122m21=ð2NÞ, which is 121= ð2NFÞ, where F1= ð1þ4NmÞ if m is small. The effective number of founders,ke, is similar to the effective population size (Ne) defined by Hallatschek and Nelson (2008) for a model of range expansion in a continuously distributed population. Like ke, Hallatschek and Nelson’sNe quantifies the rate of loss of heterozygosity at the leading edge of a range expan-sion. They estimatedNefrom simulations.
The composite parameter keincludes the effects of two opposing forces. Both the founder effect and the period of random mating after the population is founded increase the importance of genetic drift and hence reduce ke. Immigra-tion from the neighboring populaImmigra-tion—there is only one for the population most recently founded—reduces the variance in allele frequency and hence increases ke. Whether ke is larger or smaller than k depends on the balance reached. A little algebra shows that ifm1,N1, andT2N, then ke . kif 2Nm . k 2 1=2, independently ofT.
Additional generations between successive colonization events also increase the effective strength of selection. IfAis in low frequency ands16¼0, then only thefitness of hetero-zygous carriers of Ais important. We show in Appendix B that, in this case, the effective selection coefficient against heterozygotes is
s1;e¼Ts1: (10)
If s1¼0, then the effective selection coefficient againstAA individuals is
s2;e¼Ts2: (11)
Simulation Test of Realistic Model
We simulated the realistic model of range expansion de-scribed above. Each replicate begins with the frequency ofA set to the specified initial frequency, x0. Then one cycle of colonization results in a frequency x1 in population 1. A cycle consists of the sampling of gametes to form a propa-gule; selection in the propapropa-gule; creation of population 1; and then Tgenerations of migration, selection, and genetic drift in populations 0 and 1. The details of one cycle are described below. If x1 .0, the next cycle begins with the formation of the propagule that will establish population 2. Cycles continue until eitherAis lost or allnpopulations are established. Ifxn$1/(2N),Asurvived the range expansion
and the set of frequenciesfx0; . . .; xng, the allele frequency
trajectory, was retained for further analysis. This process was continued until a specified number of replicates in whichAsurvived was obtained. The probability of survival was estimated to be the ratio of the number of replicates in whichAsurvived to the total number of replicates run.
The events during one cycle are as follows. Ifipopulations have been established, then the number of copies ofAin the propagule that establishes populationi+ 1,ji+1, is generated
from a binomial distribution with probabilityxiand sample size
2k. Thus xi+1 in the propagule isjiþ1=ð2kÞ. Then migration
deterministically modifies all the allele frequencies according to
xi9¼ ð122mÞxiþmðxi21þxiþ1Þ (12)
fori¼1,. . .,i. In the two end populations (0 andi+ 1), 1–2m is replaced by 1 – m, and x21 and xiþ2 are set to 0. Then, selection deterministically changes the frequencies in all popu-lations toxj$, forj¼0,. . .,i+ 1, using Equation 2. Finally, the
frequency of Ain the next generation in each population (in-cluding population 0) is obtained by generating a binomially distributed random variate with meanxi$and sample size 2N.
To compare the simulation results from the realistic model with the Wright–Fisher model, we used the analytic theory described above withkreplaced by the integer near-est ke (Equation 9) and s1 and s2by Ts1 and Ts2. The re-striction to integer values of k is necessary because the Markov chain has to have an integer number of states.
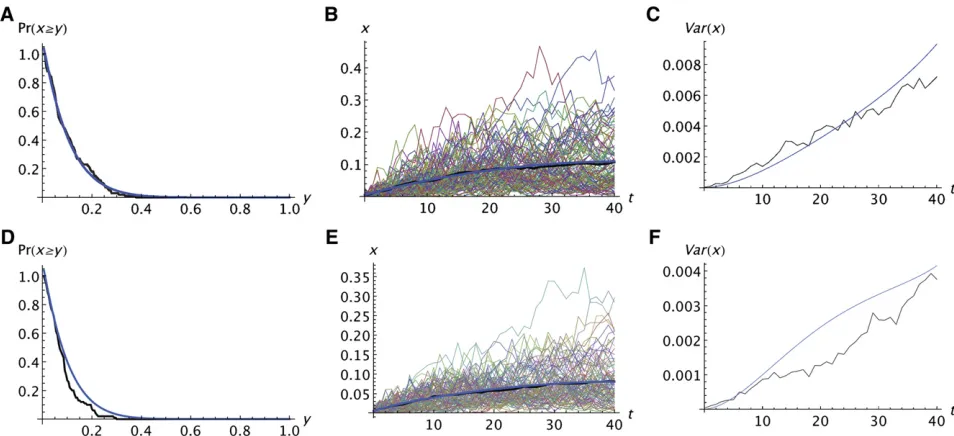
Figure 2 shows two examples of thefit of the predictions of the Wright–Fisher model to the simulation results of the realistic model without migration. Figure 2, A–C, shows the results for a neutral allele and Figure 2, D–F, shows the results for a deleterious recessive allele (s1 ¼ 0, s2 ¼ 0.03). Figure 2, A and D, compares the probability that A reaches a specified frequency. Figure 2, B and E, compares the average frequencies, using the same format as Figure 1. Figure 2, C and F, compares the variances among replicates. These results are typical for other data sets. Without migra-tion, the fit of the analytic predictions to the simulations is quite good for neutral and recessive deleterious alleles, at least for ks2,2. The predicted variances among replicates do not fit as well as the predicted averages, which is not surprising given that second moments are more variable than first moments. For selected alleles, the predicted Prðx $ yÞtends to be slightly larger than the simulated val-ues and the predictedx tends to be slightly larger than the simulated values. Those tendencies are more pronounced for alleles with an additive deleterious effect on relative
fitness (s2¼2s1), particularly if ks2.1, which is large enough that such deleterious alleles would have little chance of increasing to high frequency. The extent to which all three predicted quantitiesfit the simulations is roughly similar.
With migration, the fit of the predictions to the simu-lations is not quite as good. Four examples are shown in Figure 3. Only the results for the average frequency are presented. With migration but no selection (Figure 3A), the analytic prediction tends to be slightly less than the Figure 1 Comparison of analytic predictions with the simulation results for the idealized model described in the text. (A and B) Thin lines showxifori¼0 ton¼10 for each replicate in
whichAwas not lost before population 10. The thick black line shows the average of the 100 replicates and the thick blue line shows the ex-pectation based on the analytic theory. (C and D) Probability that an allele reaches a frequency
yin thefinal population when the range expan-sion is complete. In A–D,k¼100 and one copy of the mutant was present in the propagule founding population 1. In A and C,s1¼s2¼
average of the simulations. That tendency is also seen when there is migration and selection (Figure 3, B–D). Even when the number of colonization events is large enough thatAis
fixed in some of the replicates (Figure 3D), the predicted average frequency does not deviate by much from the ana-lytic prediction.
After the range expansion is complete, continuing migra-tion will tend to smooth patterns created by the range expansion and continuing selection will cause the frequen-cies of deleterious alleles to gradually decay. Once the last population is colonized, our approximations for the expan-sion phase no longer apply. Subsequent evolution will be governed by the effective population sizes and selection intensities in each population. If the populations are large and selection is relatively strong, the decay will roughly follow the deterministic theory of selection and migration until allele frequencies become quite small. One example is presented in Figure 4.
The analytic approximation also provides an estimate of the probability that an allele will not be lost during the range expansion. Table 1 shows that the predicted and ac-tual probabilities for the six cases shown in Figures 2 and 3 are in reasonable agreement, although the predictions tend to be larger than the simulated values.
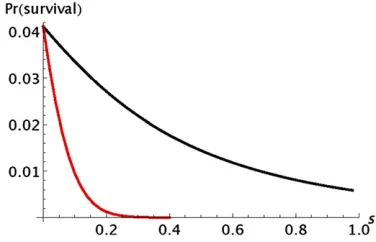
We can explore further the probability thatAwill not be lost during the range expansion. Deleterious alleles of addi-tive effect are lost quickly but deleterious recessive alleles have a substantial probability of not being lost even if their ultimate probability offixation is low. Figure 5 shows some typical results for deleterious alleles. The probability that an allele survives is much lower for an allele of additive effect than for one that has a recessive effect.
The similarity of the model of range expansion and a model of a single population leads to a simple prediction about the loss in heterozygosity during a range expansion. The heterozygosity of neutral loci will be reduced by a factor
of 121=ð2keÞin each successive population.
Continuously Distributed Populations
Our results are based on a model in which populations are discrete. Much of the interest in range expansion comes from human and other populations that are continuously distributed in space. The relationship between continuous and discrete population models is not simple. As Felsenstein (1975) first noted, it is difficult to formulate a consistent model of afinite population that is continuously distributed in space and that maintains a uniform population density. The reason is that the assumption of uniform density is not compatible with the assumption that individuals reproduce independently of one another (Sawyer 1976). The usual res-olution of this problem is to approximate a continuous model by a sequence of discrete models (Nagylaki 1978a,b).
To express our results in terms of a model of range expansion in a continuously distributed population, assume the populations in a discrete-population model are a distance lapart. Our results predict that heterozygosity decreases as a linear function of distance,HðiÞ ¼H0ð12i=ð2keÞÞ, in line with previous analytical results (DeGiorgioet al.2011). To express this result as a function of distance, d, rather than population number, we write
HðdÞ ¼H0
12 d 2ke
; (13)
Figure 2 Comparison of analytic predictions of the Wright–Fisher model with the simulation result for the realistic model with no migration. The format is the same as in Figure 1. The analytic predictions were obtained by replacingkby the integer nearestkeands1ands2byTs1andTs2. In A–F,k¼100,
whereke¼lkeindicates the net effect of genetic drift when the leading edge of the population moves a distancel.
We can relate the parameters of a discrete-population model to those of a model of a continuously distributed population as follows. A continuous-population model at equilibrium is characterized by the population density (r),
the root-mean-square dispersal distance (s), and the total length of the habitat (L). The correspondence between dis-crete and continuous models in a one-dimensional habitat is well established for populations at equilibrium. If Lis large enough that end effects do not dominate, the heterozygosity and decrease in the probability of identity-by-descent of neutral alleles in a continuous-population model are the same as in a discrete-population model when r¼N=l and
s¼lpffiffiffiffim, where l¼ L/nis the distance between adjacent populations (Malécot 1975). Therefore, to recover the parameters of the discrete-population model, for which we have an analytic approximation, N¼lr, m¼s2=l2, and n¼L=l, wherelis not yet specified.
To determinel, we assume that new individuals beyond the leading edge of the population are randomly sampled from k individuals at or near the leading edge. Range ex-pansion occurs as new individuals appear in such a way that their average density isr. This assumptionfits the observa-tion of Hallatschek et al.(2007) who found that, in an ex-perimental study of range expansion in Escherichia coli, colonists appeared to come predominantly from the small number of cells at the expanding edge of the population. In a continuously distributed population expanding at a uni-form rate, there is no delay corresponding to the T gener-ations allowed for in the discrete-population model. HenceT can be set to 1. In the continuous model, a habitat of length L is colonized in total timet, which corresponds ton gen-erations in the discrete-population model. Therefore,n¼t, which we have already determined to be L/l, and conse-quentlyl¼L/t.
With these assumptions, the ke is given by Equation 9 with T¼1 and
a¼
12s
2
l2 2
2 1
2lr; (14)
Figure 3 Comparison of analytic predictions with the simulation results for a model with finite population size and migration. The format is the same as in Figure 1, B and E. In A–D,k¼
100,N¼1000,m¼0.04, and one copy of the mutant was present in the propagule founding population 1. In A,s2¼s1¼0 (neutral); in B,
s2¼0.02 ands1¼0 (recessive deleterious); in
C,s2¼0.02 ands1¼0.01 (additive
deleteri-ous); in D,s2¼0.01 ands1¼0.005 (additive
deleterious).
Figure 4 Illustration of the effects of continued evolution after all popu-lation are colonized.k¼100,N¼1000,T¼5,s2¼0.01,s1¼0.005, and
wherel¼L/t. Therefore
ke¼ L
tða=kþ ð12aÞ=lrð12aÞÞ: (15)
The value ofkecorresponds toNeof Hallatschek and Nelson (2008). Their simulation model is more realistic and allows for the interaction of range expansion and dispersal in a way that ours does not. We are assuming weak migration and deterministic expansion of the population front.
We can estimatekefrom the regression of heterozygosity with linear distance. Ramachandranet al.(2005)fitted the regression line
HðdÞ ¼0:768226:52·1026d (16)
(wheredis the distance in kilometers from Addis Ababa) to heterozygosities computed for 783 microsatellite loci in a worldwide sample of 1027 individuals. From this regres-sion we concludeke¼1:5·105 km. To get a rough idea of what this result means, assume that modern human popu-lations expanded a total distance,L, of 25,000 km in 2000 generations (i.e., 50,000 yr assuming 25 yr per generation). This impliesl¼125 km. To make further progress we need to assume a historical equilibrium density,r, which we ar-bitrarily set to 100/km. It is reasonable to assume that the average per generation dispersal distance, s, was small
enough thats2=l2 is small. Together these assumptions im-ply thatain Equation 15 is nearly 1. Consequently,
1
1=keþ1=12;500¼
1:5·105
125 ¼1:2·10
4 (17)
orke1327. Using our simple model of range expansion in humans, we conclude that the data of Ramachandran et al. (2005) imply the expansion of modern humans into Asia and North America did not require extreme founder events at the leading edge. This application is intended to illustrate how our results can be interpreted in terms of a continuously distributed population rather than to infer details of human history. Hu-man populations did not expand their range at a uniform rate and, more importantly, the expansion had a two-dimensional component that we have not attempted to model here.
Discussion and Conclusions
We show that range expansion in a one-dimensional habitat is similar in some ways to random mating in a single popu-lation. The succession of colonization events during range expansion creates a spatial sequence of allele frequencies that is analogous to the time sequence of allele frequencies in a single population. This is true in an idealized model of range expansion and is approximately true in a more realistic model that allows for some delay before the next colonization event and for weak geneflow among established populations. The similarity of the two models allows the theory of random mating to be adapted to make analytic predictions about the consequences of range expansions. There is a strong stochastic component to the process that makes prediction of individual allele frequency trajectories difficult, but the average trajectory and the extent of variation among them are well predicted by the analytic theory.
Although our simulation results are for a model of instantaneous population growth, our analytic theory makes clear that the effective number of colonists, ke, depends partly on the net effect of genetic drift between successive colonization events and hence can be defined for other mod-els of population growth including the logistic model.
Previous work on the effects of surfing has emphasized that surfing can drive some initially rare alleles to high frequency (Traviset al.2007; Hallatschek and Nelson 2010; Hallatschek 2011). The probability that an initially rare allele isfixed in a randomly mating population can be cal-culated from a diffusion approximation (Kimura 1962). Roughly speaking, deleterious alleles have a significant probability of being fixed by genetic drift ifNs#1, where Nis the population size andsis the selection coefficient. In the context of range expansions, our approximate theory tells us that the probability that an initially rare allele is driven to fixation during a range expansion depends on the product kese, where ke is the effective propagule size (Equation 9) and se is the effective selection coefficient (Equations 10 and 11). This provides an approximate way Figure 5 Illustration of the difference between alleles with an additive
(red line) and a recessive (black line) effect onfitness. Pr(survival) is the probability that an allele initially present in one copy in population 0 is still present in populationn. For both curves,k¼n¼50 ands2¼s. For
additive selection,s1¼s/2 and for recessive selection,s1¼0. The results
were obtained by iterating the transition matrix of the Markov chain. Table 1 Predicted and actual probabilities that an allele initially present in one copy in the propagule founding population 1 will be present in populationn
Predicted Actual
Figure 2, A–C 0.048 0.043
Figure 2, D–F 0.047 0.038
Figure 3A 0.034 0.048
Figure 3B 0.047 0.031
Figure 3C 0.039 0.007
Figure 3D 0.013 0.0012
to determine whether a deleterious allele has a significant probability of surfing to a high frequency. It implies that expanding populations could accumulate deleterious muta-tions at a faster rate than equilibrium populamuta-tions, which could potentially explain the observed excess of deleterious alleles in Europeans (Lohmuelleret al.2008) or the collapse of some invading species (Coolinget al.2011).
Clines in allele frequency are often attributed to geo-graphic variation in selection intensities. In humans, clines in the frequencies of alleles that cause monogenic diseases are observed and sometimes attributed to unknown environ-mental conditions (Novembre and Di Rienzo 2009). For ex-ample, theD508 allele ofCFTRassociated with cysticfibrosis (Bertranpetit and Calafell 1996) and the C282Y mutation of hemochromatosis (Lucotte and Dieterlen 2003) have a higher frequency in northern than in southern Europe. Our results show that such clines could be created by range expansion in the absence of any geographic variation in selection inten-sity. Several authors (Handley et al. 2007; DeGiorgio et al. 2009; Hunleyet al.2009) have emphasized the importance of nonequilibrium processes in structuring human and other populations and the need to consider neutral explanations for apparently adaptive patterns.
Our theory also predicts the slope of a gradient on heterozygosity that results from range expansion in a one-dimensional habitat and can be recast in terms of a contin-uous habitat. This correspondence allows us to obtain a rough estimate of the effective propagule size on the basis of the data of Ramachandranet al.(2005).
Acknowledgments
M.S. was partially supported by a grant from the U.S. National Institutes of Health, R01-GM40282. L.E. was par-tially supported by a Swiss National Science Foundation grant, 3100A0-126074.
Literature Cited
Austerlitz, F., B. Jung-Muller, B. Godelle, and P. H. Gouyon, 1997 Evolution of coalescence times, genetic diversity and structure during colonization. Theor. Popul. Biol. 51: 148–164. Bertranpetit, J., and F. Calafell, 1996 Genetic and geographical variability in cysticfibrosis: evolutionary considerations, pp. 97– 118 inVariation in the Human Genome, edited by D. Chadwick and E. Cardew. John Wiley & Sons, New York.
Cooling, M., S. Hartley, D. A. Sim, and P. J. Lester, 2011 The widespread collapse of an invasive species: Argentine ants ( Line-pithema humile) in New Zealand. Biol. Lett. DOI: 10.1098/ rsbl.2011.1014.
Crow, J. F., and M. Kimura, 1970 An Introduction to Population Genetics Theory, Harper & Row, New York.
DeGiorgio, M., M. Jakobsson, and N. A. Rosenberg, 2009 Explaining worldwide patterns of human genetic variation using a coalescent-based serial founder model of migration outward from Africa. Proc. Natl. Acad. Sci. USA 106: 16057–16062.
DeGiorgio, M., J. H. Degnan, and N. A. Rosenberg, 2011 Coalescence-time distributions in a serial founder model of human evolutionary history. Genetics 189: 579–593.
Deshpande, O., S. Batzoglou, M. W. Feldman, and L. L. Cavalli-Sforza, 2009 A serial founder effect model for human settlement out of Africa. Proc. Natl. Acad. Sci. USA 276: 291–300.
Edmonds, C. A., A. S. Lillie, and L. L. Cavalli-Sforza, 2004 Mutations arising in the wave front of an expanding population. Proc. Natl. Acad. Sci. USA 101: 975–979.
Ewens, W. J., 2004 Mathematical Population Genetics: I. Theoret-ical Introduction. Springer-Verlag, New York.
Excoffier, L., and N. Ray, 2008 Surfing during population expan-sions promotes genetic revolutions and structuration. Trends Ecol. Evol. 23: 347–351.
Excoffier, L., M. Foll, and R. J. Petit, 2009 Genetic consequences of range expansions. Annu. Rev. Ecol. Evol. Syst. 40: 481–501. Felsenstein, J., 1975 A pain in the torus: some difficulties with
models of isolation by distance. Am. Nat. 109: 359–368. Hallatschek, O., 2011 The noisy edge of traveling waves. Proc.
Natl. Acad. Sci. USA 108: 1783–1787.
Hallatschek, O., and D. R. Nelson, 2008 Gene surfing in expand-ing populations. Theor. Popul. Biol. 73: 158–170.
Hallatschek, O., and D. R. Nelson, 2010 Life at the front of an expanding population. Evolution 64: 193–206.
Hallatschek, O., P. Hersen, S. Ramanathan, and D. R. Nelson, 2007 Genetic drift at expanding frontiers promotes gene seg-regation. Proc. Natl. Acad. Sci. USA 104: 19926–19930. Handley, L. J. L., A. Manica, J. Goudet, and F. Balloux, 2007
Go-ing the distance: human population genetics in a clinal world. Trends Genet. 23: 432–439.
Hunley, K. L., M. E. Healy, and J. C. Long, 2009 The global pattern of gene identity variation reveals a history of long-range migra-tions, bottlenecks, and local mate exchange: implications for biological race. Am. J. Phys. Anthropol. 139: 35–46.
Kimura, M., 1962 On the probability offixation of mutant genes in a population. Genetics 47: 713–719.
Klopfstein, S., M. Currat, and L. Excoffier, 2006 The fate of muta-tions surfing on the wave of a range expansion. Mol. Biol. Evol. 23: 482–490.
Li, J. Z., D. M. Absher, H. Tang, A. M. Southwick, A. M. Castoet al., 2008 Worldwide human relationships inferred from genome-wide patterns of variation. Science 319: 1100–1104.
Liu, H., F. Prugnolle, A. Manica, and F. Balloux, 2006 A geograph-ically explicit genetic model of worldwide human-settlement history. Am. J. Hum. Genet. 79: 230–237.
Lohmueller, K. E., A. R. Indap, S. Schmidt, A. R. Boyko, R. D. Hernandez et al., 2008 Proportionally more deleterious ge-netic variation in European than in African populations. Nature 451: 994–997.
Lucotte, G., and F. Dieterlen, 2003 A European allele map of the C282Y mutation of hemochromatosis: Celticvs.Viking origin of the mutation? Blood Cells Mol. Dis. 31: 262–267.
Malécot, G., 1975 Heterozygosity and relationship in regularly subdivided populations. Theor. Popul. Biol. 8: 212–241. Nagylaki, T., 1978a Random genetic drift in a cline. Proc. Natl.
Acad. Sci. USA 75: 423–426.
Nagylaki, T., 1978b The geographical structure of populations. Stud. Math. 16: 588–624.
Novembre, J., and A. Di Rienzo, 2009 Spatial patterns of variation due to natural selection in humans. Nat. Rev. Genet. 10: 745– 755.
Prugnolle, F., A. Manica, and F. Balloux, 2005 Geography predicts neutral genetic diversity of human populations. Curr. Biol. 15: R159–R160.
Sawyer, S., 1976 Branching diffusion processes in population ge-netics. Adv. Appl. Probab. 8: 659–689.
Travis, J. M. J., T. Munkemuller, O. J. Burton, A. Best, C. Dytham
et al., 2007 Deleterious mutations can surf to high densities on the wave front of an expanding population. Mol. Biol. Evol. 24: 2334–2343.
Vlad, M. O., L. L. Cavalli-Sforza, and J. Ross, 2004 Enhanced (hydrodynamic) transport induced by population growth in re-action-diffusion systems with application to population genetics. Proc. Natl. Acad. Sci. USA 101: 10249–10253.
Communicating editor: W. Stephan
Appendix A
Derivation of Effective Number of Founders
The model assumes that population 1 is founded bykindividuals from population 0 in which the frequency ofAisx0. After population 1 is founded, it grows immediately to sizeN. Each generation, it receives immigrants from population 0 at a rate mper generation forTgenerations. Let the frequency ofAin the newly founded population bex. Following the notation in Crow and Kimura (1970, Chap. 7.3), assuming the 2Ncopies are drawn with replacement,
EðxÞ ¼x0
and
E
h
ðx2x0Þ2 i
¼x0ð12x0Þ
2k ;
wherekis the number of founding individuals andE(.) denotes the expectation.
Next wefind what happens afterTgenerations of random mating with continued immigration from population 0. First, the population size grows to Nby sampling with replacement from thekfounders, which changesxto
x9¼xþe;
whereE(e) = 0 and VarðeÞ ¼xð12xÞ=2N. Migration changesx9to
x$¼ ð12mÞx9þmx0:
Therefore
Ex$¼ ð12mÞ EðxÞ þmx0¼x0:
To derive a recursion equation for the variance inxin generationt,V(t), we take the square
x$2¼ ð12mÞ2 x2þ ð12mÞ2 e2þm2x02þ2ð12mÞ2 xeþ2mð12mÞ x0xþ2mð12mÞ x0e
and the expectation of both sides. Writing the variance ofx$asV(t+ 1), we obtain
Vðtþ1Þ þx02¼ ð12mÞ2VðtÞ þx02 þ ð12mÞ2 x0ð12x0Þ2VðtÞ
2N þm
2x2
0þ2mð12mÞ x02þm2x02;
which implies
Vðtþ1Þ ¼aVðtÞ þ ð12mÞ2 x0ð12x0Þ
2N ;
wherea122m21=ð2NÞand the approximate equality assumesm,,1 andN..1, which is the case of interest in the present application.
This is a linear recursion equation that has the solution
VðtÞ ¼c1atþc2:
c1þc2¼V0
c2¼ac2þ
x0ð12x0Þ
2N ;
where we are ignoring terms of orderm/Nandm2. Therefore
c2¼
x0ð12x0Þ
2Nð12aÞ
c1¼V02x2Nð10ð12x0Þ
2aÞ:
The solution has to satisfyV0=x0(12x0)/(2k), which implies
c1¼x0ð12x0Þ
1 2k2
1 2Nð12aÞ
c2¼
x0ð12x0Þ
2Nð12aÞ:
AfterTgenerations
VðTÞ ¼x0ð12x0Þ
1 2k2
1 2Nð12aÞ
aTþx2Nð10ð12x0Þ
2aÞ
¼x0ð12x0Þ
2k a
Tþx0ð12x0Þ
2Nð12aÞ
12aT:
To define an effective number of founders, we solve
x0ð12x0Þ
2ke ¼
x0ð12x0Þ
2k a
Tþx0ð12x0Þ
2Nð12aÞ
12aT
forketo obtain
ke¼
1
aT= kþ ð12aTÞ=Nð12aÞ:
ke may be larger or smaller than k. In general ke increases with increasing m and but may increase or decrease with increasing T. Continued geneflow increases the effective number of founders because it reduces the variance inxat the time the next population is founded.
In this derivation, we have not included the effect of migration from the newly founded population back into the source of the colonists. This back migration would changex0slightly. We justify ignoring this change because it is of the same order of magnitude as the migration rate,m, and hence will modify the effect of immigration on the variance in the newly founded population by a term that is only of order m2.
Appendix B
Derivation of the Effective Selection Coefficients
To model the effect of selection during theTgenerations, we assume thatAis the deleterious allele and that the relativefitnesses of individuals with 2, 1, or 0 copies ofAare 1–s2, 1–s1, and 1. The deterministic frequency ofAafter one generation is
Dx¼s2x2ð12xÞ2s1xð12xÞð122xÞ
12s2x222s1xð12xÞ ;
wherexis the frequency ofA. Our interest is in the case in which the selection coefficients are small andAis in low frequency. Under these assumptions, whenAhas intermediate dominance (s1.0), this equation can be approximated by
which has the solution
xðTÞ ¼xð0Þð12s1ÞTxð0Þð12Ts1Þ
afterTgenerations ifs1is small. With this approximation, we can summarize the net effect of selection by replacings1by an effective selection coefficients1,e=Ts1.
WhenAis recessive (s1= 0), the equation of change can be approximated by
Dx2s2x2:
This difference equation does not have a closed-form solution but, if s2is small, it can be approximated by a differential equation that does,
dx
dt¼2s2x
2;
which has the solution
xðTÞ ¼ xð0Þ 1þs2Txð0Þ: