Modified Generalized Degree Distance of Some Graph Operations

(1)

ISSN Online: 2160-0384 ISSN Print: 2160-0368

DOI: 10.4236/apm.2018.86032 Jun. 20, 2018 548 Advances in Pure Mathematics

Modified Generalized Degree Distance of

Some Graph Operations

Shengmei Lv

School of Mathematics and Statistics, Qinghai Nationalities University, Xining, China

Abstract

The modified generality degree distance, is defined as:

( )

{ } ( )

( )

(

( ) ( )

)

*

, , G G ,

u v V G

H G d u v d u d vλ

λ

⊆

=

∑

_{which is a modification of the}

ge-nerality degree distance. In this paper, we give some computing formulas of the modified generality degree distance of some graph operations, such as, composition, join, etc.

Keywords

Degree Distance, Modified Generalized Degree Distance, Graph Operations

1. Introduction

Throughout this paper all graphs considered are finite and simple graphs. Let G

be such a graph with vertex set V G

( )

and edge set E G

( )

, and denoted by

n and m the values of V G

( )

and E G

( )

, respectively. For vertices

( )

,

u v V G∈ , the distance between u and v in G, denoted by d u vG

( )

, , is the

length of a shortest

( )

u v, -path in G, and let d vG

( )

be the degree of a vertex

( )

v V G∈ . The complement of G, denoted by G, is the graph with vertex set

( )

V G , in which two distinct vertices are adjacent if and only if they are not ad-jacent in G, and denoted by m the value of E G

( )

. We use Cn, Pn and Kn

to denote the cycle, path and complete graph on n vertices, respectively. Other terminology and notation will be introduced where it is needed or can be found in [1].

A Topological index of a graph is a real number related to the graph; it does not depend on labeling or pictorial representation of a graph. In chemistry, to-pological index is used for modeling physicochemical, pharmacologic, biological and other properties of chemical compounds [2]. One of the oldest and How to cite this paper: Lv, S.M. (2018)

Modified Generalized Degree Distance of Some Graph Operations. Advances in Pure Mathematics, 8, 548-558.

https://doi.org/10.4236/apm.2018.86032

Received: May 3, 2018 Accepted: June 17, 2018 Published: June 20, 2018

http://creativecommons.org/licenses/by/4.0/

(2)

DOI: 10.4236/apm.2018.86032 549 Advances in Pure Mathematics

well-studied distance-based graph invariants is the Wiener number W G

( )

, also termed as Wiener index in chemical or mathematical chemistry literature, which is defined [3] as the sum of distances over all unordered vertex pairs in G, namely,

( )

{ } ( )u v V G, G

( )

, .

W G d u v

⊆ =

∑

Dobrynin and Kochetova [4] and Gutman [5] introduced a new graph inva-riant with the name degree distance or Schultz molecular topological index, which is defined as follows:

( )

{ } ( )u v V G,

(

G

( )

G

( )

)

G

( )

, .

DD G d u d v d u v

⊆

=

∑

+

In [6], Gutman and Klavzar defined product-degree distance as follow:

( )

{ } ( )u v V G,

(

G

( )

G

( )

)

G

( )

, .

DD G∗ d u d v d u v

⊆

=

∑

⋅

Note that the degree distance and product-degree distance are degree-weight versions of the Wiener index. We encourage the interested readers to consult [7] [8][9] for Wiener index. In [4][10][11][12][13][14], there are more conclu-sions for degree distance, which shows that the research of degree distance is a hot topic. In [15], Sagan et al. computed some exact formulae for the Wiener polynomial of various graph operations containing Cartesian product, composi-tion, join, disjunction and symmetric difference of graphs, whose concepts will be presented in later part. In [16], Hamzeh et al. consider the generalized degree distances of some graph operations. The generalized degree distance of a graph is defined as follow [17]:

( )

{ } ( )u v V G,

( )

,

(

G

( )

G

( )

)

.

H G d u v d uλ d v

λ

⊆

=

∑

+ ₍₁₎

For a real number λ_{, the modified generalized degree distance, denoted by}

( )

*

H Gλ , is also defined in [17]:

( )

{ } ( )

( )

(

( ) ( )

)

*

, , G G .

u v V G

H G d u v d u d vλ

λ

⊆

=

∑

₍₂₎

If λ =0_, H Gλ

_{( )}

=4m and H Gλ*

( )

=4m2. When λ =1, H Gλ

( )

=DD G

( )

and _{H G}*

( )

_{DD G}*

( )

λ = , which implies that the generalized degree distance is equal to the degree distance (or Schultz index), and the modified generalized degree distance is equal to the product-degree distance. Therefore the study of this new topological index is important and we try to obtain some new results related to this topological index.

In this paper, we show that the explicit formulas for _{H G}*

( )

λ of some graph operations containing the composition, join, disjunction and symmetric differ-ence of graphs, and we apply the results to compute the modified generality de-gree distance of some special graphs.

Next, we introduce four types of graph operations:

(3)

2

V and edge sets E1, E2 is the graph union G G1 2 together with all the

edges joining V1 and V2.

The composition G G G= 1

[ ]

2 of graphs G1 and G2 with disjoint vertex

sets V1 and V2 and edge sets E1 and E2 is the graph with vertex set V V1× 2

and u=

(

u v1, 1

)

is adjacent with v=

(

u v2, 2

)

whenever (u1 is adjacent with 2

u ) or (u u1= 2 and v1 is adjacent with v2), see [18].

The disjunction G H∨ _{of graphs}_G_and_H_{is the graph with vertex set}

( )

V G V H× _and

(

u v₁, ₁

)

is adjacent with

(

u v2, 2

)

whenever u u1 2∈E G

( )

or v v1 2∈E H

( )

.

The symmetric difference G H⊕ _{of two graphs}_G_and_H_{is the graph with}

vertex set V G V H

( )

×

( )

and

(

) (

{

1, 2

)(

1, | 2

)

1 1

( )

or 2 2

( )

but not both

}

E G H⊕ = u u v v u v E G∈ u v ∈E H .

In the final of this section, we present several well-known indices: the first Zagreb index M G1

( )

and the second Zagreb index M G2

( )

[19], the first

Zagreb conindex M G1

( )

and the second Zagreb coindex M G2

( )

[20], which

will be used in our results.

( )

(

( )

)

2

1 G , 1 G G .

u V G uv E G

M G d u M G d u d v

∈ ∈/

=

∑

=

∑

+

( )

(

( ) ( )

)

( )

(

( ) ( )

)

2 G G , 2 G G .

uv E G uv E G

M G d u d v M G d u d v

∈ ∈/

=

∑

=

∑

In fact, M G1

( )

can be also expressed as a sum over edges of G,

( )

(

( )

)

1 G G .

uv E G

M G d u d v

∈

=

∑

+

2. Main Results

The purpose of this section is to compute the modified generalized degree dis-tance for four graph operations. We begin with the following crucial lemma re-lated to distance properties of some graph operations.

Lemma 2.1. [18][21]Let G and H be two graphs, then we have: 1) V G H

(

∨

)

= V G H

(

[ ]

)

=V G H

(

⊕

)

=V G V H

( )

⋅

( )

,

(

)

( )

2

( )

2

( )

2 ,

E G H∨ = E G V H⋅ + E H V G⋅ − E G E H⋅

(

)

( )

,

E G H+ = E G + E H +V G V H⋅

(

)

( )

2

( )

2

( )

4 ,

E G H⊕ = E G V H⋅ + E H V G⋅ − E G E H⋅

[ ]

(

)

( )

2

( )

.

E G H = E G V H⋅ + E H V G⋅

2) The join, composition, disjunction and symmetric difference of graphs are associative and all of them are commutative except from composition.

3)

( )

(

( )

)

0

, 1 or or &

2 otherwise, G H

u v

d + u v uv E G uv E H u V G V V H

 =



=_ ∈ ∈ ∈ ∈

(4)

4) [ ]

(

( ) ( )

)

( )

,

0 & , , ,

1 &

2 & , G

G H

d a c a c a c b d

d a b c d

a c bd E H a c bd E H

 ≠

 ₌ ₌



=  ₌ _∈



 ₌ _∈/



5)

(

( ) ( )

)

( )

0 &

, , , 1 or

2 otherwise,

G H

a c b d

d ∨ a b c d ac E G bd E H

= =

 

= ∈ ∈

 

6)

(

( ) ( )

)

( )

0 &

, , , 1 or but not both

2 otherwise,

G H

a c b d

d ⊕ a b c d ac E G bd E H

= =

 

= ∈ ∈

 

7)

( )

,

G G H

H

d a V H a V G d a

d a V G a V H

+

 + ∈

 = 

+ ∈



8) dG H_{[ ]}

(

( )

a b,

)

=V H d a

( ) ( )

G +d bH

( )

,

9) dG H⊕

(

( )

a b,

)

=V H d a

( ) ( )

G +V G d b

( )

H

( )

−2d a d bG

( ) ( )

H ,

10) d_{G H}∨

(

( )

a b,

)

= V H d a

( ) ( )

_G +V G d b d a d b

( )

_H

( )

− _G

( ) ( )

_H .

Proof. The parts 1) - 5) are consequence of definitions and some well-known results of the book of Imrich and Klavzar [18]. For the proof of 6) - 10) we refer to [21]. ■

For a given graph Gi, we denote ni and mi by the number of vertices and

edges, respectively. Then we can obtain the modified generalized degree distance of the join graph G G1+ 2 as following:

Theorem 2.1. Let G1 and G2 be two graphs. Then

(

)

(

( )

)

(

)

( )

(

)

*

1 2 2 1 1 1 1 2 2 1 2 2

2 2

2 1 1 2 2 1 1 1 1 2 2 1

2 2

2 2 1 2 1 2 1 1 2 2 2 1 1 2

2 2

4 2 2 .

H G G n M G n M G M G M G

n m n m n M G n M G M G

M G m m n n m n n m n m n m

λ λ

λ

+ = + + +

+ + + + +

+ + + + + + +

Proof. In the graph G G1+ 2, we can partition the set of pairs of vertices of

1 2

G G+ _{into three subsets}A A₁, ₂ and A3. In A1, we collect all pairs of

ver-tices u and v such that u is in G1 and v is in G2. Hence, they are adjacent in

1 2

G G+ _{. The sets} A₂ and A3 are the set of pairs of vertices u and v which are

in G1 and G2, respectively. Therefore, we can partition the sum in the

formu-la of *

(

)

1 2

H G Gλ + into three sums Si such that Si is over Ai for i=1,2,3.

By 3) and 7) of Lemma 2.1, we have

( ) ( )

( )

(

( )

)

(

( )

)

(

)

1 2 1 2

1 2

*

1 2 1

1 2 2 2 1 1 2 2

,

4 2 2 .

G G G G u V G v V G

S d u v d u n d v n m m n n m n n m

λ

+ ∈ ∈

= + +

= + + +

∑ ∑

{ } ( )

( )

(

( )

)

(

( )

)

( )

(

( )

)

(

( )

)

( )

(

( )

)

(

( )

)

( )

(

)

( )

1 2 1 1

1

1 1 1 1

1 1

*

2 2 2

,

2 2 2 2

2 2

2 1 2 1 1 2 1 2 1 2 1 1 2 1

,

2

2 .

G G G G u v V G

G G G G

uv E G uv E G

S d u v d u n d v n

d u n d v n d u n d v n M G n M G n m M G n M G n m

λ

+ ⊆

∈ ∈/

= + +

= + + + + +

∑

(5)

{ } ( )

( )

(

( )

)

(

( )

)

( )

(

( )

)

(

( )

)

( )

(

( )

)

(

( )

)

( )

(

)

( )

1 2 2 2

2

2 2 2 2

2 2

*

3 1 1

,

1 1 1 1

2 2

2 2 1 1 2 1 2 2 2 1 1 2 1 2

,

2

2 .

G G G G u v V G

G G G G

uv E G uv E G

S d u v d u n d v n

d u n d v n d u n d v n M G n M G n m M G n M G n m

λ

+ ⊆

∈ ∈/

= + +

= + + + + +

∑

Therefore,

(

)

( )

(

)

(

)

( )

(

)

* * * *

1 2 1 2 3

2 2

2 1 1 1 1 2 2 1 2 2 2 1 1 2

2 1 1 1 1 2 2 1 2 2 1 2

2 2

1 2 1 1 2 2 2 1 1 2

2 2

4

2 2 .

H G G S S S

n M G n M G M G M G n m n m

n M G n M G M G M G m m

n n m n n m n m n m

λ

λ λ

+ = + +

= + + + + +

+ + + + +

■

In the above theorem, if λ =1, then we can obtain *

(

)

1 2

DD G G+ _{. Replace}

separately G1 and G2 by K1 and G in Theorem 2.1, we can obtain the

fol-lowing result.

Corollary 2.2. Let G be a connected graph with n vertices and m edges. Then

(

)

(

( )

)

(

( )

)

* 2

1 2 1 2 1 2 2 .

H K G λ M G M G m M G M G n nm m

λ + = + + + + + + +

We can observe that M C1

( )

n =4n for n≥3, M P1

( )

n =4n−6 for n>1,

and M C1

( )

n =2n n

(

−3

)

,

( ) (

)

2

1 n 2 2

M P = n− _{. Hence, we can compute the}

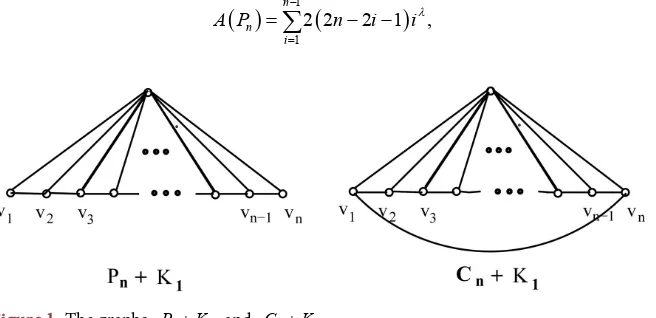
formulae for modified generalized degree distance of fan graph K P1+ n and

wheel graph K C1+ n (see Figure 1) in the following.

Example 2.1. *

(

)

1

(

2

) (

2

)

1 n 2 9 39 44 3 7 15 .

H K P λ n n n n

λ + = − − + + + −

(

)

(

)

(

)

* 1

1 n 2 9 3 3 3 .

H K C λ n n n n

λ + = − − + +

Next, we compute the exact formula for the modified generalized degree dis-tance of the composition of two graphs. Before starting the discussion, we first denote by A G

( )

the sum _{i j}i jn, 1=d u u d uGλ

(

i, j

)

G

( )

i

≠

∑

. It is easy to deduce that

(

)

( )

(

) ( )

, 1 , , 1 ,

n n

i j _G _i _j _G _i i j _G _i _j _G _j i j d u u d u i j d u u d u

λ λ

= =

≠ = ≠

∑

.

By calculations we obtain the expressions for A P

( )

n and A C

( )

n as

follow-ing:

( )

1

(

)

1

2 2 2 1 ,

n n

i

A P − n i iλ

=

[image:5.595.211.539.558.717.2]

=

∑

− −

(6)

( )

1 2 1 2

1 1 2

1

4 , is odd,

2 4 , is even.

n i n _n i ni n A C

n ni n

λ

λ λ λ

− = − − + =   =   ₊ 

∑

we can also obtain the expressions for *

( )

n

H Pλ and H Cλ*

( )

n :

( ) (

)

1

(

)(

)

*

2

2 1 n 8 1 .

n

i

H Pλ n λ i n i λ

− = = − +

∑

− −

( )

1 2 1 * 2 2 1

8 , is odd,

4 8 , is even.

2 n i n n i ni n H C n

n ni n

λ λ λ λ − = − =   =  _{ }  _{ } ₊    

∑

These formulae are similar to the known results in [22]:

( )

1 1 1

1 1 ,

n n

n

i i

W P n iλ iλ

λ − − + = = =

∑ ∑

−

( )

1 2 1 1 2 2 1

, is odd,

, is even. 2 n i n n i

n i n

W C

n _n _i _n

λ λ λ λ − = + − =   = _{ } _{ } ₊   

∑

[ ]

(

)

(

( )

)

( )

(

)

( )

* 2

1 2 2 2 1 1 1 2 2 2 1 1 2

2 2 1 1 1 1 2 1 2 2

2 2 4 *

2 2 1 2 1 2 1

2 2

2

4 4 .

H G G n m M G n M G n m M G

n m M G m M G n M G

n m A G m W G n H G

λ λ λ λ = + + + + + + + +

Proof. Set V G

( )

1 =

{

u u1, , ,2 un1

}

and V G

( )

2 =

{

v v1, , ,2 vn2

}

. By 4), 8) of Lemma 2.1 and definition of _{H G}*

( )

λ , we have

[ ]

(

)

{ } ( [ ]) [ ]

( )

(

[ ]

( )

[ ]

( )

)

( ) ( ) [ ]

(

)

(

)

(

( )

)

( )

(

)

( ) [ ]

(

) (

)

(

( )

(

)

( ) ( )

)

1 2 1 2 1 2

1 2 1 2 1 2 1 2 1 2 1 1 1 2 2

2 2 2 2

*

1 2 ,

2

, ,

2

2 2

, 1 2 2

1

,

1 _, _, _,

2

, , ,

i k j l

k l

G G G G G G

u v V G G

i k j l G i G k

G G u v u v

G j G l

n n

k l G G p k p l G p G p

p

v v E G

G k G l G k G l

H G G d u v d u d v

d u v u v n d u d v

n d u d v

d u v u v n d u n d u

d v d v d v d v

λ λ λ λ ⊆ = = ∈ = = + ⋅ + = + ⋅ + +

∑

∑ ∑

[ ]

(

)

(

)

(

( )

( ) ( )

( )

( ) ( )

)

( ) [ ]

(

)

(

)

(

( )

(

( )

)

( ) ( )

)

2 1 1 1 1 2

1 2 1 2 2 2

1 2

1 1 2

2

1 2 2 2 2

2

, 1 2

, 1

2 2

, 1 2

1 2 , , , , , , k l n n

i j G G i k j l G i G j k l

i j

G i G l G j G k G k G l

n n

k l G G i k j l G p

p

v v E G

G p G k G l G k G l

d u v u v n d u d u

n d u d v n d u d v d v d v

d u v u v n d u

n d u d v d v d v d v

λ λ = = ≠ = = ∈/ + + + + + + + +

∑ ∑

( )

(

)

(

( )

)

( )

2

2 2 1 1 1 2 2 2 1 1 2 2 2 1 1

2 2 4 *

1 1 2 1 2 2 2 2 1 2 1 2 1

2 2 2

4 4

n m M G n M G n m M G n m M G m M G n M G n m A G m W G n H G

λ

λ λ

= + + +

+ + + + +

(7)

In Theorem 2.3, *

(

[ ]

)

*

(

[ ]

)

1 2 1 2

H G Gλ =DD G G if λ =1, and in the above

proof, when u ui= j & v v E Gk l∈

( )

2 , dG G1 2[ ]

(

u vi, k

)

,

(

u vj, l

)

=1; when u ui≠ j,

[ ]

(

)

(

)

1

(

)

1 2 i, k , j, l G i, j

G G

d u v u v =d u u _{; when} u u_i= _j & v v E G_{k l}∈/

_{( )}

₂ , [ ]

(

)

(

)

1 2 i, k , j, l 2

G G

d u v u v = _{by Lemma 2.1 4).}

By composing paths or cycles with various small graphs, we can obtain classes of polymer-like graphs. As an application, we give the formulae of *

(

[ ]

)

2

n

H P Kλ and *

(

[ ]

)

2

n

H C Kλ , where P Kn

[ ]

2 and C Kn

[ ]

2 are open fence graph and

closed fence graph (see Figure 2), respectively.

Example 2.2. *

(

[ ]

)

4

(

*

( )

)

( )

2 25 32 2 4 ,

n n n n

H P Kλ = n− + H Pλ +A P + W Pλ

[ ]

(

)

(

( )

)

( )

* 4 *

2 25 8 2 4 .

n n n n

H C Kλ = n− + H Cλ +A C + W Cλ

The following theorem characterizes the modified generalized degree distance of the disjunction of two graphs.

(

)

(

)

( )

(

)

( )

(

( )

)

( )

(

)

( )

(

( )

)

( )

( ) ( )

(

)

*

1 2

2 2

2 2 2 2 2 2 1 1 1 1 1 1 2 2

2 2

2 2 1 1 1 1 1 2 1 2 2 1 1 1 1 2

1 2 2 1 2 2 1 1 1 1 1 1 2 2

1 2 1 1 1 2 1 1 1 1 2 2 1 2 1 1

2 2 4 2 4

2 2

H G G

n n n m m M G n n n m m M G

n m M G n m M G n n m M G m M G

M G n M G M G M G n M G M G

n n M G M G n M G M G n M G M G

λ λ

λ

∨

= + − + + −

+ + + +

+ − + −

+ − −

( ) ( )

)

(

)

( )

(

)

( )

(

)(

)

( )

(

)(

)

( )

( ) ( )

2 2 2 2 2

2 1 2 2 2 1 2 1 2 1 1 2 2 2 1 1

2 2 2

2 1 1 1 1 2 2 2 2 2 2 1

2 2

1 1 1 1 2 2 1 2 1 1 1 2

1 1 1 2 2 2 1 2 2 1 2 1 2 2

4 4 2 2

2 2 4

4

.

M G M G n m m n m m n m n m M G

n m n m M G n m n m M G

n m n m M G n n M G M G

n M G M G n M G M G M G M G

+ + + + −

+ − + − −

+ − − −

+ + −

[image:7.595.264.493.501.711.2]

Proof. By the definition of G G1∨ 2, we first present the following four sums:

(8)

DOI: 10.4236/apm.2018.86032 555 Advances in Pure Mathematics { } ( ) ( )

(

( )

)

( )

(

)

{ } ( ) ( )

( ) ( )

{ } ( ) ( )

( )

{ } ( ) ( )

(

( )

)

1 2 1 2

1 2

1 2 1 2

1 1

1 2

2 2

1 2

1 2 1 2

1 2

*

1 , 2 1

2 1 2 2 , 2 1 , 1 2 ,

G G G G

x y V G uv E G

G G G G

G G

x y V G uv E G

G G

x y V G uv E G

G G G G

x y V G uv E G

S n d x n d u d x d u

n d y n d v d y d v

n d x d y

n d u d v

n n d x d v d y d u

⊆ ∈ ⊆ ∈ ⊆ ∈ ⊆ ∈ = + − ⋅ + − = + + +

∑

{ } ( ) ( )

( ) ( )

(

( )

)

{ } ( ) ( )

( )

(

( )

)

{ } ( ) ( )

( ) ( ) ( ) ( )

(

)

( )

(

)

( )

1 1 2 2

1 2

2 2 1 1

1 2

1 1 2 2

1 2 2 , 1 , , 2

2 2 2 2

2 1 2 2 1 1 1 1 2 1 1 2 2

( )

4 2 2 2

G G G G

x y V G uv E G

G G G G

x y V G uv E G

G G G G

x y V G uv E G

n d x d y d u d v

n d u d v d x d y

d x d y d u d v

n m m n m n m M G n m M G

⊆ ∈ ⊆ ∈ ⊆ ∈ − + − ⋅ + + = + − + −

∑

( ) { } ( )

(

( )

( ) ( )

)

( )

( ) ( )

(

)

( ) { } ( )

( ) ( )

( ) { } ( )

( ) ( )

( ) { } ( )

(

( ) ( )

)

1 2 1 2

1 2

1 2 1 2

1 1

1 2

2 2

1 2

1 2 1 2

1 2

*

2 , 2 1

2 1 2 2 , 2 1 , 1 2 ,

G G G G

xy E G u v V G

G G G G

G G

xy E G u v V G

G G

xy E G u v V G

G G G G

xy E G u v V G

S n d x n d u d x d u

n d y n d v d y d v

n d x d y

n d u d v

n n d x d v d y d u

∈ ⊆ ∈ ⊆ ∈ ⊆ ∈ ⊆ = + − ⋅ + − = + ⋅ + +

∑

( ) { } ( )

( ) ( )

(

( )

)

( ) { } ( )

( ) ( )

(

( )

)

( ) { } ( )

( ) ( ) ( ) ( )

(

)

( )

(

)

( )

1 1 2 2

1 2

2 2 1 1

1 2

1 1 2 2

1 2 2 , 1 , , 2

2 2 2 2

1 2 1 1 2 2 2 1 1 2 2 2 1

4 2 2 2

G G G G

xy E G u v V G

G G G G

xy E G u v V G

G G G G

xy E G u v V G

n d x d y d u d v

n d u d v d x d y

d x d y d u d v

n m m n m n m M G n m M G

∈ ⊆ ∈ ⊆ ∈ ⊆ − + − ⋅ + + = + − + −

∑

( ) ( )

(

( )

( ) ( )

)

( )

( ) ( )

(

)

( ) ( )

(

( ) ( )

)

1 2 1 2

1 2

1 2 1 2

1 1

1 2

2 2

1 2

1 2 1 2

1 2

*

3 2 1

2 1 2 2 2 1 1 2

G G G G

xy E G uv E G

G G G G

G G

xy E G uv E G

G G

xy E G uv E G

G G G G

xy E G uv E G

S n d x n d u d x d u

n d y n d v d y d v

n d x d y

n d u d v

n n d x d v d y d u

∈ ∈ ∈ ∈ ∈ ∈ ∈ ∈ = + − ⋅ + − = + + +

∑

( ) ( )

(

( )

)

( ) ( )

(

( )

)

( ) ( )

( ) ( ) ( ) ( )

( )

( ) ( )

( )

( ) ( )

1 1 2 2

1 2

2 2 1 1

1 2

1 1 2 2

1 2

2

1

2

2 2 2 1 1 2 1 1 1 2 2 1 2 2 1

2

1 1 2 2 1 1 1 2 2 2 1 2 2

G G G G xy E G uv E G

n d x d y d u d v n d u d v d x d y d x d y d u d v n m M G n n M G M G n M G M G

n m M G n M G M G M G M G

∈ ∈ ∈ ∈ ∈ ∈ − + − + + = + − + − +

∑

( ) ( )

(

( )

( ) ( )

)

( )

( ) ( )

(

)

( ) ( )

(

( )

( ) ( )

)

1 2 ₁ ₂ ₁ ₂

1 2 1 2

1 2

*

4 2 1

2 1

2

xy E G uv E G _G _G _G _G

x y u v

G G G G

xy E G u V G

S n d x n d u d x d u

n d y n d v d y d v

n d x n d u d x d u

(9)

( )

( ) ( )

(

)

( ) ( )

(

( )

( ) ( )

)

( )

( ) ( )

(

)

1 2 1 2

1 2

1 2 1 2

2 1

2

G G G G

G G G G x V G uv E G

G G G G

n d y n d v d y d v

n d x n d u d x d u n d y n d v d y d v

λ ∈ ∈/ ⋅ + − + + − ⋅ + −

∑

(

)

( )

(

)

( )

(

)

( )

)

( ) ( )

(

)

(

( )

(

)

( )

(

( )

)

( )

)

( ) ( )

3 2 3 2

2 2 2 2 2 2 1 1 1 1 1 1 2 2

2 2

1 2 2 1 1 1 1 2 1 1 1 2 2 2 1 1

1 2 1 1 1 2 1 1 2 1 1 2 1 1 1 2

1 2 2 1 2 2 1 1 1 1 1 1 2 2

2 1 2 2

2 2 4 2 4

2 2

2 .

n n m n m M G n n m n m M G

n n m M G m M G n m M G n m M G

M G M G

λ λ λ = + − + + − + + + + + − − + − + − +

Thus, we can obtain the result of Theorem 2.4 by the formula

(

)

* * * * *

1 2 1 2 4 3

H G Gλ ∨ =S +S +S S− . ■ Finally, we consider the modified generalized degree distance of the symme-tric difference of two graphs.

(

)

(

)

( )

(

)

( )

(

( )

(

( )

)

( )

(

)

( )

(

( )

)

( )

( ) ( )

* 1 2 2 2

2 2 2 2 2 2 1 1 1 1 1 1 2 2

2 2

2 2 1 1 1 1 1 2 1 2 2 1 1 1 1 2

1 2 2 1 2 2 1 1 1 1 1 1 2 2

1 2 1 1 2 2 1 1 1 1 2 2 1 2 1 1

2 2 8 2 8

2

2 2 2 2 2

2 2

H G G

n n n m m M G n n n m m M G

n m M G n m M G n n m M G m M G

λ λ λ ⊕ = + − + + − + + + + + − + − + − −

( ) ( )

)

(

)

( )

(

)

( )

(

)(

)

( )

(

)(

)

( )

( ) ( )

2 2 2 2 2 2

2 1 2 2 2 1 2 1 2 1 1 2 2 2 1 1

2 2 2

2 1 1 1 1 2 2 2 2 2 2 1

2 2

1 1 1 1 2 2 1 2 1 1 1 2

1 1 1 2 2 2 1 2 2 1 2 1 2 2

2 4 4 2 4

2 4 2 8

2 8 2

4 4 8 .

M G M G n m m n m m n m n m M G

n m n m M G n m n m M G

n m n m M G n n M G M G

n M G M G n M G M G M G M G

+ + + + −

+ − + − −

+ − − −

+ + −

Proof. Similar to the proof of Theorem 2.4, we consider four sums:

{ } ( ) ( )

(

( )

)

( )

(

)

(

)

( )

(

)

( )

1 2 1 2

1 2

1 2 1 2

*

1 , 2 1

2 1

2

2 2 2 2

2 1 2 2 1 1 1 1 2 1 1 2 2

4 2 4 4 .

G G G G

x y V G uv E G

G G G G

S n d x n d u d x d u

n d y n d v d y d v

n m m n m n m M G n m M G

⊆ ∈ = + − ⋅ + − = + − + −

∑

( ) { } ( )

(

( )

)

( )

(

)

(

)

( )

(

)

( )

1 2 1 2

1 2

1 2 1 2

*

2 , 2 1

2 1

2

2 2 2 2

1 2 1 1 2 2 2 1 1 2 2 2 1

4 2 4 4 .

G G G G

xy E G u v V G

G G G G

S n d x n d u d x d u

n d y n d v d y d v

n m m n m n m M G n m M G

∈ ⊆ = + − ⋅ + − = + − + −

∑

( ) ( )

(

( )

)

( )

(

)

( )

( ) ( )

( )

1 2 1 2

1 2

1 2 1 2

*

3 2 1

2 1

2

2 2 2 1 1 2 1 1 1 2 2 1 2 2 1

2

1 1 2 2 1 1 1 2 2 2 1 2 2

2

2 4 .

G G G G xy E G uv E G

G G G G

S n d x n d u d x d u n d y n d v d y d v

n m M G n n M G M G n M G M G n m M G n M G M G M G M G

(10)

( ) ( )

(

( )

( ) ( )

)

( )

( ) ( )

(

)

(

)

( )

(

)

( )

(

)

( )

)

1 2 1 2 1 2

1 2 1 2

*

4 2 1

2 1

3 2 3 2

2 2 2 2 2 2 1 1 1 1 1 1 2 2

2 2

1 2 2 1 1 1 1 2 1 1 1 2 2 2 1 1

2

2 2 8 2 8

2

xy E G uv E G G G G G

x y u v

G G G G

S n d x n d u d x d u

n d y n d v d y d v

n n m n m M G n n m n m M G

n n m M G m M G n m M G n m M G

λ

∈/ ∈/

≠ ≠

= + −

⋅ + −

= + − + + −

+ + + +

∑

( ) ( )

(

)

(

( )

(

)

( )

(

( )

)

( )

)

( )

1 2 1 1 1 2 1 1 2 1 1 2 1 1 1 2

1 2 2 1 2 2 1 1 1 1 1 1 2 2

2

2 1 2 2

2 2 2

2 2 2 2

2 .

n n M G M G n M G M G n M G M G M G n M G M G M G n M G M G

M G M G

λ

λ+

+ − −

+ − + −

+

Therefore, we can obtain the result of Theorem 2.5 by

(

)

* * * * *

1 2 1 2 4 2 3

H G Gλ ⊕ =S +S +S − S . ■ Remark. In Section 2, we present the explicit formulae of the modified gene-ralized degree distance for four types of graph operations containing G G1+ 2,

[ ]

1 2

G G , G G1∨ 2 and G1⊕G2, and we give some examples. It implies that our

results are convenient to compute the modified generalized degree distance of these graph operations. Moreover, if λ =1_{, then}_{H G}*

( )

_{DD G}*

( )

λ = . This

im-plies that our results are related to the product-degree distance. In [16] Hamzeh

et al. construct graph polynomial as following:

(

)

{ } ( )

(

( ) ( )

)

( ), *

,

, d u v.

G G u v V G

H G xλ d u d v x λ

⊆ =

∑

It is easy to see that the results of our Theorems 2.1, 2.3, 2.4 and 2.5 are exactly the first derivatives at point x=1_{of the graph polynomial} _{H G x}*

(

_,

)

λ . Thus we obtain the relation between the modified generalized degree distance polynomial and Wiener-type invariant polynomial for graphs.

Funding

This work is supported by the National Natural Science Foundation of China (11761056) and by Natural Science Foundation of Qinghai Province (2018-ZJ-717), and by the Fund of Qinghai Nationalities University (2016XJG08).

References

[1] Bondy, J. and Murty, U. (1976) Graph Theory with Applications. Elsevier, New York. https://doi.org/10.1007/978-1-349-03521-2

[2] Gutman, I. and Polansky, O. (1986) Mathematical Concepts in Organic Chemistry. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-642-70982-1

[3] Wiener, H. (1947) Structural Determination of Paraffin Boiling Point. Journal of the American Chemical Society, 69, 17-20. https://doi.org/10.1021/ja01193a005

[4] Dobrynin, A. and Kochetova, A. (1994) Degree Distance of a Graph: A Degree Analogue of the Wiener Index. Journal of Chemical Information and Computer Sciences, 34, 1082-1086. https://doi.org/10.1021/ci00021a008

[5] Gutman, I. (1994) Selected Properties of the Schultz Molecular Topogical Index.

Journal of Chemical Information and Computer Sciences, 34, 1087-1089.

(11)

[6] Gutman, I. and Klavzarć, S. (1997) Wiener Number of Vertex-Weighted Graphs and a Chemical Applications. Discrete Applied Mathematics, 80, 73-81.

https://doi.org/10.1016/S0166-218X(97)00070-X

[7] Gutman, I. (1997) A Property of the Wiener Number and Its Modifications. Indian Journal of Chemistry: Section A, 36, 128-132.

[8] Gutman, I., Rada, J. and Araujo, O. (2000) The Wiener Index of Starlike Trees and a Related Partial Order. MATCH Communications in Mathematical and in Comput-er Chemistry, 42, 145-154.

[9] Hua, H. (2009) Wiener and Schultz Molecular Topological Indices of Graphs with Specified Cut Edges. MATCH Communications in Mathematical and in Computer Chemistry, 16, 643-651.

[10] Dankelmann, P., Gutman, I., Mukwembi, S. and Swart, H.C. (2009) On the Degree Distance of a Graph. Discrete Applied Mathematics, 157, 2773-2777.

https://doi.org/10.1016/j.dam.2009.04.006

[11] Feng, L., Liu, W., Ili, A. and Yu, G. (2013) Degree Distance of Unicyclic Graphs with Given Matching Number. Graphs and Combinatorics, 5, 449-462.

https://doi.org/10.1007/s00373-012-1143-5

[12] Ilić, A., Stevanović, D., Feng, L., Yu, G. and Dankelmann, P. (2011) Degree Distance of Unicyclic and bicyclic Graphs. Discrete Applied Mathematics, 159, 779-788.

[13] Tomescu, I. (2008) Properties of Connected Graphs Having Minimum Degree Dis-tance. Discrete Math, 309, 2745-2748. https://doi.org/10.1016/j.disc.2008.06.031

[14] Tomescu, I. (2010) Ordering Connected Graphs Having Small Degree Distances.

Discrete Applied Mathematics, 158, 1714-1717.

[15] Sagan, B., Yeh, Y. and Zhang, P. (1996) The Wiener Polynomial of a Graph. Inter-national Journal of Quantum Chemistry, 60, 959-969.

https://doi.org/10.1002/(SICI)1097-461X(1996)60:5<959::AID-QUA2>3.0.CO;2-W

[16] Hamzeh, A., Iranmanesh, A. and Hossein-Zadeh, S. (2013) Some Results on Gene-ralized Degree Distance. Open Journal of Discrete Mathematics, 3, 143-150.

https://doi.org/10.4236/ojdm.2013.33026

[17] Hamzeh, A., Iranmanesh, A., Hossein-Zadeh, S. and Diudea, M. (2012) Generalized Degree Distance of Trees, Unicyclic and Bicyclic Graphs. Studia Universitatis Babeș-Bolyai. Chemia, 4, 73-85.

[18] Imrich, W. and Klavzarć, S. (2000) Product Graphs: Structure and Recognition. John Wiley & Sons, New York.

[19] Gutman, I. and Trinajstic, N. (1972) Graph Theory and Molecular Orbitals. Total

φ-Electron Energy of Alternant Hydrocarbons. Chemical Physics Letters, 17, 535-538. https://doi.org/10.1016/0009-2614(72)85099-1

[20] Došlić, T. (2008) Vertex-Weighted Wiener Polynomials for Composite Graphs. Ars Mathematica Contemporanea, 1, 66-80.

[21] Khalifeh, M., Yousefi-Azari, H. and Ashrafi, A. (2008) The Hyper-Wiener Index of Graph Operations. Computers & Mathematics with Applications, 56, 1402-1407.

https://doi.org/10.1016/j.camwa.2008.03.003

[22] Hossein-Zadeh, S., Hamzeh, A. and Ashrafi, A. (2009) Wiener-Type Invariants of Some Graph Operations. Filomat, 29, 103-113.