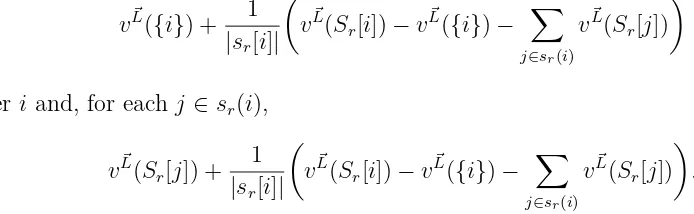The sequential equal surplus division for sharing a river

Munich Personal RePEc Archive

The sequential equal surplus division for

sharing a river

Béal, Sylvain and Rémila, Eric and Solal, Philippe

14 March 2012

Online at

https://mpra.ub.uni-muenchen.de/37346/

The Sequential Equal Surplus Division for Sharing a River

Sylvain B´eal†_{, Amandine Ghintran}‡_{, Eric R´emila}§_{, Philippe Solal}∗∗

March 14, 2012

Abstract

We introduce the sequential equal surplus division for sharing the total welfare result-ing form the cooperation of agents along a river with a delta. This allocation rule can be seen as a generalization of the contribution vectors introduced by Ju, Borm and Ruys [2007] in the context of TU-games. We provide two axiomatic characterizations of the sequential equal surplus division.

Keywords: Amalgamation – Consistency – Fairness – Sequential Equal Surplus Division – Sharing a river.

JELClassification number: C71, D63, D74, Q25, Q56.

1

Introduction

L→

In this article, we consider the distribution of a scarce resource among a set of agents that are partially ordered. This kind of situations is particularly well illustrated by the problem of sharing water from a river with a delta among a group of agents located along this river. Between each pair of neighbors along the river there is an additional flow of water that flows from upstream to downstream. Water inflow at the territory of downstream agents cannot be consumed by upstream agents and agents located at other branches of the river. The benefit of each agent depends on the amount of water he consumes at his location. An optimal water allocation maximizes the total benefits. Cooperation among the riparian agents is often necessary to achieve the optimal allocation of water since the upstream agents may have to let pass some water to the downstream agents if the latter have a higher marginal benefit from consuming water. Monetary transfers among the agents can sustain the optimal allocation of water. A welfare distribution yields a utility for each agent, which is equal to his benefit from the water consumption plus his monetary transfer. Historically, distributing the optimal welfare that arises from the river water consumption has been at the center of international tensions and conflicts. The international law suggests several equity notions as guidelines for resolving international water disputes. Unfortunately, as explained in Kilgour and Dinar (1995)

∗_{Financial support the National Agency for Research (ANR) — research programs “Models of Influence and}

Network Theory” ANR.09.BLANC-0321.03 and “Math´ematiques de la d´ecision pour l’ing´enierie physique et sociale” (MODMAD) — is gratefully acknowledged.

†_{Corresponding author. Universit´e de Franche-Comt´e, CRESE, 30 Avenue de l’Observatoire, 25009}

Be-san¸con, France. E-mail: sylvain.beal@univ-fcomte.fr. Tel: (+33)(0)3.81.66.68.26. Fax: (+33)(0)3.81.66.65.76

‡_{Universit´e Lille 3, EQUIPPE, France. E-mail: amandine.ghintran@gmail.com.}

§_{Universit´e de Lyon, LIP, UMR 5668 CNRS-ENS Lyon-Universit´e Lyon 1, France. E-mail:}

eric.remila@ens-lyon.fr. Tel: (+33)(0)4.26.23.38.14. Fax: (+33)(0)4.72.72.80.80

∗∗_{Universit´e de Saint-Etienne, CNRS UMR 5824 GATE Lyon Saint-Etienne, France. E-mail:}

and Wolf (1999), these principles are often difficult to apply and even contradictory, especially for river, which constrain transfers because of the direction of the flow.

One approach to the problem of finding a fair welfare distribution is to model the situation as a cooperative digraph TU-game as in Ambec and Sprumont (2002) and Khmelnitskaya (2010). The river with a delta and the location of each agent along the river are highlighted by a digraph on the set on riparian agents. The worth of each connected coalition is given by the social welfare that it can secure for itself without the cooperation of the agents located upstream and at different branches of the river. The worth of each other coalition is defined by the sum of the worths of their maximally connected parts.

Different allocation rules for distributing the social welfare resulting from the optimal water allocation in digraph TU-games are discussed in the literature. These rules are characterized by translating into axioms the above-mentioned principles of international law. The views expressed in the three doctrines advocated in international disputes are the efficiency of water use, the Absolute Territorial Sovereignty (ATS for short) and Territorial Integration of all Basin States (TIBS for short). Efficiency of the water use means that the optimal social welfare is fully shared among the agents. The ATI doctrine states that a country has absolute sovereignty over the area of any river basin on its territory. The TIBS doctrine attributes an equal use of water to all agents whatever their contribution to the flow. Within the cooperative game theoretical framework, efficiency of the water use is obviously the usual property of efficiency of the allocation rule. The combination of efficiency and the ATS doctrine has been very often translated into the property that the welfare distribution should be core-stable. The various game-theoretical interpretations of TIBS accords different shares of the surplus resulting from the cooperation of a coalition of agents.

In this article we introduce an allocation rule, the sequential equal surplus division as we call it, which relies on a weaker interpretation of the ATS doctrine and a more flexible interpretation of the TIBS doctrine. In particular, we would like to insist on four features of the sharing river problem.

First, although the core-stability is a nice requirement for an allocation rule, it is too strong if one sticks to the original statement of the ATS doctrine. In fact, the ATS doctrine only requires a stability condition for every singleton coalitions. The sequential equal surplus division satisfies the weaker interpretation of the ATS doctrine that each individual agent should get a payoff at least equal to the welfare he can secure without the cooperation of any other agent. The sequential equal surplus division is not core-stable but satisfies the intuitive stability property that a coalition containing an agent and all the agents located downstream obtains at least the welfare it can achieve without the cooperation of the other agents. This property is very similar to the subsidy-free property used in Aadland and Kolpin (1998).

studied in van den Brink et al. (2012), violate this very basic and intuitive requirement. On the contrary, it is satisfied by the sequential equal surplus division introduced in this article.

Third, we aim at generalizing the well-accepted principle of the standard solution to n -agent sharing river situations. The construction of the sequential equal surplus division is done sequentially by following the natural direction of the river’s flow. At the spring/root of the river, the water can possibly flow through several branches. Together with the groups of agents located on each of these branches, the agent located at the spring of the river achieves some surplus compared to the situation in which each branch would behave selfishly. This surplus is precisely the difference between the total welfare and the sum of the welfare achieved separately by the rooted agent and each of the downstream branches. In order to distribute this surplus, the rooted agent as well as the cooperating coalitions corresponding to the downstream branches of the river can be considered as single entities. As in the two-agent case, the participation of each entity is necessary for the production of the welfare surplus. Therefore, it seems natural to give to each entity an equal share of the surplus in addition to the welfare it can guarantee in the absence of cooperation. This is equivalent to reward each entity by the well-known equal surplus division for TU-games. For each remaining branch of the river, the obtained total payoff is what remains to be shared among its members. This payoff is in the spirit of the individual standardized remainder vector introduced by Ju et al. (2007) for the class of TU-games. The sequential equal surplus division then consists in applying repeatedly the above step to all agents located at the roots of the remaining branches considered as single entities. The distribution of the surplus of cooperation between two or more coalitions of agents is also at the heart of the construction of many of the solutions proposed in the literature. Either this surplus is fully allocated to only one agent as in the downstream incremental distribution, the upstream incremental distribution and their generalizations or it is shared on a more egalitarian basis as in the equal loss property solution studied in van den Brink et al. (2007). In any of these solutions, only the most upstream agent of the downstream coalition and the most downstream agent of the upstream coalition get a share of the surplus. Contrary to the sequential equal surplus division, these solutions somehow ignore the crucial role of the other participating agents in the coalitions located on the downstream branches.

Fourth, since the sharing river problem is represented by a digraph TU-game, we think that it is desirable to adapt several well-known principles used in cooperative (graph) TU-games to account for one-directionality of the river’s flow. Such desirable principles include consistency, fairness and amalgamation considerations as studied, among others, by Thomson (2011), Myerson (1977) and Lehrer (1988) respectively. The first and the third principles are left out of the existing literature1_{. In this article, they are adapted to digraph TU-games and are}

employed to provide two axiomatic characterizations of the sequential equal surplus division. The rest of the article is organized as follows. Section 2 is devoted to the game-theoretical definitions. The river sharing problem and its associated digraph TU-game are defined in section 3. Section 4 introduces the sequential equal surplus division and states a first result which describes some of its properties. Several properties for an allocation on the class of all digraph TU games are presented in section 5. Section 6 contains the two axiomatic characterizations.

1

2

Preliminaries : TU-games on directed graphs

For any finite set A, the notation|A| stands for the cardinality of A. The inclusion relation is denoted by ⊆ and its strict part by ⊂.

Acooperative game with transferable utility (TU-game) is a pair (N, v) consisting of a finite player (or agent) set N of sizen ∈N_{and a coalition function v : 2}N _−→R_{satisfying v(∅) = 0.}

An element S of 2N _{is a coalition, andv(S) is the maximal worth that the members of S can} obtain by cooperating. The class of all TU-games is denoted byC. For each nonempty coalition

S ∈2N_{, thesubgame of (N, v) induced by S is the TU-game (S, v}

|S) such that for any T ∈2S,

v|S(T) =v(T). A TU-game (N, v) is superadditive if v(S∪T) ≥ v(S) +v(T) for any pair of disjoint coalitions S and T. In TU-game (N, v) ∈ C each player i ∈ N may receive a payoff

zi ∈R. Apayoff vectorz = (z1, . . . , zn)∈Rn lists a payoffzi for eachi∈N. For any nonempty coalition S ∈ 2N _{the notation z}

S stands for Pi∈Szi. An allocation rule Φ on C is a map that assigns to each TU-game (N, v)∈ C a payoff vector Φ(N, v)∈Rn_.

The cooperation structure on the player set N is specified by a graph. A graph on N is a subsetLof all unordered pairs{{i, j} ⊆N :i6=j}. Each element{i, j}ofLis called a link with ends iand j. We will use the shorthand notationij to designate a link{i, j} ∈L. The links of the graphs represent the communication possibilities between pairs of players and thus affect the formation of coalitions. A path of length k in (N, L) is a finite sequence of distinct players (i0, i1, . . . , ik) if iqiq+1 ∈L for eachq ∈ {0, . . . , k−1}. A cycle in (N, L) is a finite sequence of

players (i0, i1, . . . , ik, i0) such that k≥2, (i0, i1, . . . , ik) is a path and iki0 ∈L. A graph (N, L)

is acyclic if it does not contain any cycle. For each subset of players C ⊆ N, the subset of links L(C) ⊆L represents the set of communication links between players in C, and the pair (C, L(C)) is thesubgraph of (N, L) induced byC. The induced subgraph (C, L(C)) of a graph (N, L) is connected if there exists at least one path between any pair of distinct players in C. By extension we say that coalitionC is connected in (N, L). The induced subgraph (C, L(C)) is maximally connected if it is connected and for eachi∈N\Cthe subgraph (C∪ {i}, L(C∪ {i})) of (N, L) is not connected. If (C, L(C)) is a maximally connected subgraph of (N, L), C is a

component of (N, L). Denote by N/L the set of components of (N, L) and by C/L(C) the set of components of the subgraph (C, L(C)) of (N, L) induced by C ⊆N. Note that if (N, L) is acyclic, then there is exactly one path between any pair of distinct players who belong to the same component. An acyclic graph is called a forest. If the forest has exactly one component, it is called a tree. Therefore, each component of a forest induces a tree. It follows from these remarks that the class of acyclic graphs on N is closed under link deletion, i.e. if (N, L) is a forest or a tree and ij ∈L, then the graph (N, L\ij) is a forest onN.

A digraph L~ on N is a graph L on N in which each link is assigned a direction, one end being designed its tail and the other its head. An edge with tailiand headj is called a directed link and is denoted by i → j. We also say that i is a predecessor of j and j is a successor of

i in L~. A digraph reflects the idea that two players incident to a communication link do not have equal access or control to that link.

Given a forest (N, L), a rooted tree L~r_{(C) on the induced subgraph (C, L(C)) is a digraph} on C that arises from a component C ∈ N/L by selecting player r ∈ C, called the root, and directing all links of L(C) away from the root r. Note that each agent r ∈ C is the root of exactly one rooted tree L~r_{(C). Note also that for any rooted tree} ~_Lr_{(C) on (N, L) and any} agent i∈C\{r}, there is exactly one directed link j → i; agent j is the unique predecessor of

sr(i) the possibly empty set of successors of playeriin~Lr. We will also use the notation sr[i] to denote the union of sr(i) and{i}. All players having the same predecessor are called brothers. We denote byBr(i) the set of all brothers ofiinL~r(C). A playerj is asubordinateofiin~Lr(C) if there is a directed path from itoj,i.e. if there is a sequence of distinct agents (i0, i1, . . . , il) such thati0 =i,il =j and for eachq∈ {0,1, . . . , l−1},iq+1 ∈sr(iq). The set Sr[i] denotes the union of the set of all subordinates ofi inL~r _{and {i}. So, we haves}

r(i)⊆Sr[i]\{i}. If a player

j is a subordinate of i, then we say that i is a superior of j. The set Pr[i] denotes the union of the set of all superiors of i in L~r _{and {i}. So, we have p}

r(i)∈Pr[i]\{i} for each i6=r. The

depth of an agent i∈C is the length of the directed path from r toi. Thedepth of the tree is the depth of its deepest agents. For an illustration of these definitions, see Figure 1 on Section 3.1. For the sake of notations, we will useL~ to denote a digraph in which each component is a rooted tree and we will precise the designated component C and root r when necessary.

A digraph TU-game is a TU-game (N, vL~_{) ∈ C in which the coalition function v}L~ _takes explicitly into account the restrictions on coalition formation induced byL~. More precisely,v~L_is the graph-restricted game introduced by Myerson (1977) where the worth of each non connected coalition is equal to the sum of the worths of its components. Formally, vL~ _{assigns to each} connected coalitionS a worth vL~_{(S), and for each other coalitionS,v}~L_{(S) =}P

T∈S/L(S)v

~ L_(T). Denote by C0 the class of all digraph TU-games where the underlying digraph is a collection of

rooted trees.

3

The river sharing problem

3.1

Sharing a river with a delta

Consider a finite set N of agents of size n ∈ N _{located along an international river. At the}

location of each agenti∈N, rainfall and inflow from tributaries increase the total river flow by

ei ∈R+. Water inflow at the territory of downstream agents cannot be consumed by upstream

agents. Following Khmelnitskaya (2010), we assume that the river can have a delta. Under these assumptions, the river is shaped like a rooted tree. More precisely, consider first an undirected tree as in Figure 1 (a). A rooted-tree arises from it by selecting an agent, called the root, and directing all edges away from this root. Then add the inflow of water on each agent location in order to obtain a river with delta as in Figure 1 (b) where the root 1 is the spring of the river.

4 5

3 1

2

4 5

3 1

2

e4

e5

e3

e2

e1

(a) (b)

Figure 1: (a) An undirected tree L – (b) A river with a deltaL~.

including himself is S1[1] = {1,2,3,4,5}, whereas the set of successors of agent 3 is s1(3) =

{4,5} and S1[3] = s1[3]. Agent 1 has no predecessor and the predecessor of agent 3 is agent

1: p1(3) = 1. The set of superiors of agent 4 including himself is P1[4] = {1,3,4} and set of

superiors of agent 5 including himself P1[5] ={1,3,5}. Agents 4 and 5 are brothers since they

have the same predecessor: p1(4) = p1(5) = 3. We thus have B1(4) = {5} and B1(5) ={4}.

This is also true for agents 3 and 2. We have B1(2) = {3} and B1(3) = {2}. The deepest

agents in the rooted tree are 4 and 5. Their depth is equal to 2.

Each agent i ∈ N is endowed with a benefit function bi : R+ −→ R that assigns to each

amount xi ∈R+ of water consumed the benefitbi(xi)∈R.

Assumption 1 (A1). The water inflow e1 is strictly positive. Each benefit function bi is strictly increasing, strictly concave, continuously differentiable on R_{++,bi(0) = 0, and the first}

derivative b(1)_i (xi) tends to +∞ asxi vanishes.

A consumption planx= (xi)i∈N ∈Rn+ satisfies the following constraints:

∀k ∈N, X

j∈Pr[k]

xj ≤

X

j∈Pr[k]

ej, and

X

j∈Pr[k]∪Br(k)

xj ≤

X

j∈Pr[k]∪Br(k)

ej. (1)

The first constraints in (1) indicate that each agent k ∈ N consumes at most the sum of the water inflow at his location and the water inflows not consumed by his upstream agents

l ∈ N. The second constraints in (1) indicate that the set of brothers of any agent k ∈ N

including himself do not consume more water than the total inflow of water available to them. A consumption plan x induces the social welfare P

i∈Nbi(xi); x is optimal if it maximizes the social welfare. Under (A1) there is a unique optimal consumption plan.

In order to reach the optimal consumption plan, some agents may refrain from consuming water. In turn, monetary compensations can be set up for these agents, which allow Pareto improvements. More precisely, money is available in unbounded quantities to perform side-payments. A compensation for agent i ∈ N is an amount of money ti ∈ R. If ti > 0, then agent i is a net beneficiary of monetary transfers; if ti < 0, then agent i is a net contributor to monetary transfers. A compensation scheme is a profile t = (ti)i∈N ∈ Rn of monetary transfers satisfying the budget constraint P

i∈Nti ≤ 0. A budget constraint is balanced if transfers add to zero. Agents value both water and money and are endowed with a quasi-linear utility function ui : R+ × R −→ R that assigns to each pair (xi, ti) ∈ R+ × R the utility

ui(xi, ti) = bi(xi) +ti. A welfare distribution is a pair (x, t) where x is a consumption plan and

t is a compensation scheme. The welfare distribution (x∗_{, t) is Pareto optimal if and only if x}∗

is the optimal consumption plan and the budget constraint is balanced. Each agent i receives the payoff zi = ui(x∗i, ti), and the sum of these payoffs is equal to the optimal social welfare

P

i∈Nbi(x∗i). The problem is to find a fair distribution of this social welfare.

3.2

The river TU-game

flow, each arc i →j is controlled by the tail i. Indeed, by refusing to pass water to j, agent i

does not cooperate with j. The definition of the coalition function vL~ _{takes into account this} fact. Since the total worth to distribute is equal to the optimal social welfare, the worth of the grand coalitionN is given byvL~_{(N) =} P

i∈Nbi(x∗i). Further a group of agents on the river can cooperate if and only if it is connected in the undirected tree L. The worth of each connected coalition S is given by the social welfare that it can secure for itself without the cooperation of the agents who are not a member of this coalition. Therefore, for any connected coalition S in

~

L, the worth v~L_{(S) is given by:}

vL~(S) = X k∈S

bk(xSk),

where xS _{= (x}S

i)i∈S solves

maxX k∈S

bk(xk) s.t. ∀k ∈S,

X

j∈Pr[k]∩S

xj ≤

X

j∈Pr[k]∩S

ej,

X

j∈Pr[k]∪Br(k)∩S

xj ≤

X

j∈Pr[k]∪Br(k)∩S

ej. (2)

Assumption (A1) ensures that there is a unique solution to this program. If the coalition is not connected, then its worth is the sum of the worths of its connected components. IfS ∈2N _{is not} connected, then it admits a unique partition into components. Agents belonging toN\Sdo not cooperate with S and act non-cooperatively. Since each benefit function is strictly increasing in the water consumed, each agent located between two components of S will consume all the water inflow entering at his location. Therefore, a component ofS will never receive the water left over by another component located upstream. It follows that the worth of a non connected coalitionS is the sum of the worths of its components and so the river TU-game (N, vL~_{) belongs} to C0. Note also that a river TU-game is superadditive.

By allocating a payoff zi to each i ∈N, we determine a compensation scheme t as follows: for each i ∈ N, ti = zi −bi(x∗i). If zN = v~L(N), then the optimal social welfare is integrally allocated among the agents andtis budget balanced. The difficulty is thus to find an agreement on the allocation of the social welfare resulting from an optimal consumption plan, which in turn determines monetary compensations.

4

The sequential equal surplus division

water use efficiency and the extended interpretation of the ATS doctrine implies core stability. The third principle listed in Kilgour and Dinar (1995) is the doctrine of “Territorial Integration of all Basin States” (TIBS). Symmetrically, this principle favors downstream agents to which it accords “equal” use, without regard to their contribution to the flow. Ambec and Sprumont (2002) apply an extreme case of the TIBS doctrine, called the “Absolute Territorial Integrity” (ATI). It aims at protecting downstream agent by stating that each agent has the right to all upstream water. Translated into game theoretical terms, this doctrine indicates that each coalition of agents should get a total payoff as least equal to the worth that it can secure for itself when the upstream agents let pass all the water flow. In the context of a river without a delta – the river is shaped like a line – Ambec and Sprumont (2002) show that there is a unique efficient allocation rule that satisfies both the ATS and ATI doctrines. van den Brink et al.

(2007) provide an axiomatic characterization of this solution. They also discuss this solution and note that it favors too much the downstream agents. Indeed, upstream agents can stop the cooperation with the downstream agents by consuming their total water inflow and so can claim much more than they get under the solution designed by Ambec and Sprumont (2002).

In this article we look at solutions that can be motivated by the ATS and TIBS doctrines, but with a more flexible interpretation of the TIBS doctrine. The general TIBS doctrine states that given an agent, this agent and his downstream neighbors are entitled to receive a share of the surplus they generate when they decide to cooperate. A very popular allocation rule that satisfies these two principles in a broader sense for the the two-agent situation is the standard solution. It assigns first to an agent his stand-alone worth and then distributes an equal share of the left surplus created by the cooperation. Rephrased in terms of the river sharing problem, the standard solution assigns first to each agent the benefit of consuming the water inflow entering his own territory and then allocates half of the surplus that can be created by the two agents when they coordinate their water consumption. That is, agent i∈ {1,2} gets:

vL~({i}) + v ~

L_({12})−v~L_({2})−vL~_({1})

2

Since the river TU-game is superadditive, vL~_({12})−vL~_({2})−vL~_{({1}) ≥ 0, which implies} that each agent gets at least his stand-alone payoff: the ATS principle is well satisfied. On the other hand, since the surplus resulting from cooperation is equally distributed among them, the TIBS principle is also satisfied. That’s why we think that a desirable property for a solution on the class of river TU-games is that it implements the standard solution in the two-agent situation. In section 6, we will translate this requirement into a property.

We would like to generalize this principle from the two-agent situation to the situation where n agents are located along a river with a delta. There is a major difference between a river shaped like a line (Ambec and Sprumont, 2002) and a river with a delta (Khmelnitskaya, 2010). When the river is shaped like a line, agents are totally ordered by the direction of the river’s flow. In a river with a delta, the direction of the river’s flow generates a partial order over the set of agents. Any pair of brothers in a rooted tree have the same position in the sense neither is the subordinate of the other. Therefore, the sequential nature of the individual decisions is more complex. We incorporate this characteristic to our solution.

So, assume that a set of agents N of size n > 2 are located along a river with a delta. Denote by r its spring or root. Pick any agent i ∈ N and focus on the welfare produced by this agent and all his subordinates. The worth vL~_(S

threaten to consume all the water inflow available to him instead of letting some water flows out toward his subordinates; but on the other hand, his subordinates may need to get extra water from i in order to achieve an optimal consumption plan among themselves. In other words, agent i and each coalition of agents Sr[j] for each j ∈ sr(i) have to cooperate in order to produce the total worth vL~_(S

r[i]). In the absence of cooperation, the total welfare achieved by these agents reduces to:

v~L({i}) + X j∈sr(i)

vL~(Sr[j]).

If one considers each coalition Sr[j] as a single entity in the problem of distributing the total welfare v~L_(S

r[i]), then it is natural to apply the equal surplus division to such a |sr[i]|-agent situation. We have:

vL~({i}) + 1 |sr[i]|

vL~(Sr[i])−v ~

L_({i})− X

j∈sr(i)

vL~(Sr[j])

to player i and, for each j ∈sr(i),

v~L(Sr[j]) + 1 |sr[i]|

v~L(Sr[i])−v ~

L_({i})− X

j∈sr(i)

v~L(Sr[j])

.

The allocation rule that we construct consists in a sequential application of the equal surplus division principle from upstream to downstream, which means that for agent i and his subor-dinates, it might remain more than v~L_(S

r[i]) to share. Before defining formally this allocation rule, we provide an example.

4 3 1

2

e4 e3

e2

e1

Figure 2: A river with a deltaL~.

Example 2 Consider the river represented by the rooted tree L~ in Figure 2. Initially the four agents cooperate with each other and the welfare vL~_{({1,2,3,4}) is to be distributed. The}

agents receive their payoff sequentially according to their distance to the spring of the river. We compute the payoff of agent 1 first on the basis of what would happen if he refuses to cooperate. In such a case, the grand coalition would partition into three coalitions: {1}, {2}

and {3,4}, where {3,4} acts as single entity. How much should agent 1 get from the worth

vL~_{({1,2,3,4}) as he refuses to cooperate? No doubt these three entities should first get the}

total worth they can secure without the cooperation of the other agents, i.e. v~L_{({1}), v}L~_({2})

and v~L_{({3,4}), respectively. As for the surplusv}L~_{({1,2,3,4})−v}~L_({1})−vL~_({2})−v~L_({3,4}),

one can argue that since agent 1 is now negotiating with coalition{2}and with coalition {3,4}

for 3-agent TU-games can be applied so that each party should get a third of the joint surplus. Consequently, agent 1 obtains his individual worth plus a third of the the joint surplus:

v~L({1}) + 1 3

v~L({1,2,3,4})−vL~({1})−vL~({2})−vL~({3,4})

.

The welfare shares remaining for coalitions {2} and {3,4}, which we call the egalitarian re-mainders for {2} and {3,4}, are given respectively by:

vL~({2}) + 1 3

vL~({1,2,3,4})−vL~({1})−v~L({2})−v~L({3,4})

(3)

and

vL~({3,4}) + 1 3

vL~({1,2,3,4})−vL~({1})−v~L({2})−v~L({3,4})

.

Then, the above procedure has to be repeated on each branch of the river with respect to the direction of the river’s flow. Thus both remaining coalitions {2} and {3,4} behave indepen-dently on their own branch of the river in order to negotiate the allocation of their respective remainder. On the one hand, agent 2 is the unique agent on his branch of the river so that the final payoff of 2 is given by (3). On the other hand, agent 3 can now be considered as the spring of the branch of the river on which he is located. As above, the egalitarian remainder for agent {4} will be:

vL~({4})+1 2

vL~({3,4})+1 3

vL~({1,2,3,4})−vL~({1})−v~L({2})−v~L({3,4})

−vL~({3})−vL~({4})

,

while agent 3 will get:

vL~({3})+1 2

vL~({3,4})+1 3

vL~({1,2,3,4})−vL~({1})−v~L({2})−v~L({3,4})

−vL~({3})−vL~({4})

.

Extending this argument to each n-agent river TU-game, we obtain a solution on the class of all river TU-games with a delta, called thesequential equal surplus division. For convenience, we define this solution on the domain of all digraph TU gamesC0. This means that if the digraph

has several components, then we treat each component as an independent river. The sequential equal surplus division on C0, denoted by Φe, is defined as follows. Pick any (N, vL~) ∈ C0, any

component C ∈N/L, any i∈C, and define theegalitarian remainder α for coalition Sr[i] as:

α(Sr[i]) =

            

v~L_{(C) if i=r,}

v~L(Sr[i]) +

α(Sr[pr(i)])−

X

j∈sr(pr(i))

vL~(Sr[j])−v ~ L_({p

r(i)})

|sr[pr(i)]|

otherwise.

(4)

Note that by definition i ∈ sr(pr(i)) for each i 6= r. The sequential equal surplus division assigns to each i∈C, C∈N/L, the payoff given by:

Φe_i(N, vL~) =vL~({i}) + 1 |sr[i]|

α(Sr[i])−

X

j∈sr(i)

vL~(Sr[j])−v ~ L_({i})

The allocation rule Φe_{generalizes the individual standardized remainder vectors proposed by} Ju, Borm and Ruys (2007) for the class of TU-games. Each individual standardized remainder vector is constructed from a bijection over the player set. Because a bijection induces a total order on the player set, it is isomorphic to a line. In this special case, the resulting individual standardized remainder vector coincides with (4). The allocation rule defined by Ju, Borm and Ruys (2007) and called the consensus value, is the average, over the set of bijections on the player set, of the individual standardized remainder vectors. There are two major differences with our allocation rule. First, the river’s flow defines a unique partial order on the player set. Secondly, more than two coalitions negotiate to share a surplus when the river continues on different branches.

Let us verify that the sequential equal surplus division is an efficient allocation rule and provides a compromise between the ATS and TIBS doctrines.

We show below that for each coalition formed by an agent and his subordinates, the egal-itarian remainder is fully redistributed among its members, i.e. for each i ∈ N, it holds that Φe

Sr[i](N, v ~

L_{) = α(S}

r[i]). For each component C ∈ N/L with root r, we have Sr[r] = C,

α(C) = v~L_{(C) by (4) and so Φ}e C(N, v

~

L_{) = v}L~_{(C), which proves (component) efficiency.}

The ATS doctrine prescribes that each agentihas the right to all water on this territory, i.e.

Φe i(N, v

~

L_)≥v~L_{({i}). This doctrine can be extended to all coalitions. In our case this doctrine} is guaranteed only for coalitions formed by an agent and his subordinates, i.e. for eachi∈N, it holds that Φe

Sr[i](N, v ~

L_)≥v~L_(S

r[i]).Therefore, a coalition consisting of any agent and all his subordinates obtains a share of the total welfare that is at least as large as the welfare they can achieve without the cooperation of their superiors in the river. Note that this property is similar to the subsidy-free property used in Aadland and Kolpin (1998) for the related problem of sharing the cleaning costs of a polluted river.

The TIBS doctrine states that each agent has the right to all water flowing along the component of the river where he lives, no matter where it enters in this component. This means that each agent has the right to a certain share of the total welfare resulting from the cooperation of all members of this component. This share is measured by the non-negative difference Φi(N, v

~

L_)−v~L_{({i})≥0 given by (5).}

These properties are summarized in the following proposition and stated for all digraph TU-games.

Proposition 1 For each digraph TU-game (N, v~L_{)∈ C}

0, each component C ∈ N/L and each

agent i∈C, it holds that: (i) Φe

Sr[i](N, v ~

L_{) =α(S} r[i]).

If, furthermore, (N, vL~_{)∈ C}

0 is superadditive, then it holds that:

(ii) α(Sr[i])≥v~L(Sr[i]);

(iii) Φi(N, vL~)≥vL~({i}).

Proof. Pick any river TU-game (N, vL~_{)∈ C}

0, any component C ∈N/L with root r∈N,and

any i∈N. The proof of part (i) is by induction on the number of subordinates of i.

Initial step_{: Assume that agent i has no subordinates, i.e. Sr[i] ={i}. Thus, sr(i) =∅ and}

(5) imply:

Φe

Sr[i](N, v ~

L_{) = Φ}e i(N, v

~

L_{) =α({i}).}

Induction hypothesis_{: Assume that the assertion holds whenSr[i] contains at mostq <|C|}

Induction step_{: Assume that Sr[i] containsq+ 1 elements. Then:}

Φe_Sr[i](N, vL~) = Φe_i(N, v~L) + X j∈sr(i)

Φe_Sr[j](N, vL~).

Since j ∈ sr(i), each Sr[j] contains at most q elements. By the induction hypothesis, the right-hand side of the above equality is equivalent to:

Φe_i(N, vL~) + X j∈sr(i)

α(Sr[j]).

Using the definition (4) of the egalitarian remainder and the fact that for each j ∈ sr(i),

pr(j) =i, the previous expression can be rewritten as follows:

vL~({i}) + 1 |sr[i]|

α(Sr[i])−

X

j∈sr(i)

vL~(Sr[j])−v ~ L_({i})

+ X

j∈sr(i)

v~L(Sr[j]) + 1 |sr(i)|+ 1

α(Sr[i])−

X

k∈sr(i)

vL~(Sr[k])−v ~ L_({i})

= vL~({i}) + 1 |sr[i]|

α(Sr[i])−

X

j∈sr(i)

vL~(Sr[j])−v ~ L_({i})

+ X

j∈sr(i)

v~L(Sr[j]) + |sr(i)|

|sr[i]|

α(Sr[i])−

X

k∈sr(i)

vL~(Sr[k])−v ~ L_({i})

= α(Sr[i]).

Therefore, we get:

Φe_Sr[i](N, vL~) = Φe_i(N, vL~) + X j∈sr(i)

α(Sr[j])

= α(Sr[i]),

as desired.

The proof of part (ii) is by induction on the depthq of the agents in (C, ~L(C)).

Initial step_{: Assume thatq = 0 so thatiis the rootrof the directed tree onC,i.e. Sr(r) =C.}

By (4), we get α(C) =v~L_{(C), as desired.}

Induction hypothesis_{: Assume that the assertion is true for eachi∈C such that his depth}

is inferior or equal to q < dC where dC is the depth of the rooted tree (C, ~L(C)).

Induction step_{: Pick any i ∈ C such that his depth is q + 1. It follows that the number}

of links on the path from the root r to pr(i) is equal to q. By the induction hypothesis and superadditivity of vL~_{, we get:}

α(Sr(i)) = v ~ L_(S

r[i]) + 1 |sr[pr(i)]|

α(Sr[pr(i)])−

X

j∈sr(p(i))

v~L(Sr[j])−v ~ L_({p

r(i)})

≥ vL~_(S r[i]) +

1 |sr[pr(i)]|

vL~_(S

r[pr(i)])−

X

j∈sr(pr(i))

vL~_(S

r[j])−v ~ L_({p

r(i)})

as desired.

The proof of part (iii) follows from (ii), the definition (5) of Φe _{and the superadditivity of}

vL~_{. It suffices to note that the collection of coalitions S}

r[j], j ∈ sr(i), and the singleton {i}

constitute a partition of Sr[i].

It is interesting to compare our solution to the solutions provided by Ambec and Sprumont (2002), van den Brink et al. (2007) for a river shaped like a line and their extension to a river with a delta provided by Khmelnitskaya (2010). Assume first that the river is shaped like a rooted tree, then the solution suggested by Khmelnitskaya (2010) is the so-called hierarchical outcome introduced by Demange (2004) and defined by:

∀i∈N, hi(N, v ~

L_{) = v}L~_(S r[i])−

X

j∈sr(i)

vL~(Sr[j]). (6)

Each agent’s payoff is equal to his marginal contribution to all his subordinates when he joins them. In case the river is shaped like a line, each agent other than agent n located at the sink of the river has exactly one successor i+ 1, so that Sr[i] = {i, i+ 1, . . . , n} and Sr[i+ 1] = {i+ 1, i+ 2, . . .} for {i+ 1}=sr(i). The hierarchical outcome reduces to:

hn(N, v ~

L_{) =v}~L_{({n}) and for i∈N\{n}, h} i(N, v

~

L_{) =v}L~_{({i, . . . , n})−v}L~_{({i+ 1, . . . , n}).}

As shown by Demange (2004), van den Brinket al. (2007) and Khmelnitskaya (2010), this solu-tion possesses several advantages. First it is efficient and satisfies also point (ii) in Proposisolu-tion 1 not only for coalitions formed by an agent and all his subordinates but for all coalitions, which means that this solution is core-stable. It also gives an incentive for an agent to cooperate with his subordinates in the sense that all the surplus resulting from this cooperation is allocated to his agent. Indeed, this surplus is given by:

vL~(Sr[i])−

X

j∈sr(i)

vL~(Sr[j])−v ~ L_({i})

and i exactly gets

vL~({i}) +v~L(Sr[i])−

X

j∈sr(i)

v~L(Sr[j])−v ~ L_({i}).

This solution is the opposite of the solution suggested by Ambec and Sprumont (2002) for a river shaped like a line, which distributes all the surplus resulting from the cooperation of an agent with his superiors to this agent:

the root gets v~L({r}) and each other agent i gets vL~({1,2, . . . , i})−v~L({1,2, . . . , i−1}).

Another way to compare (6) with our solution is to use point (i) of Proposition 1. Indeed, for each i∈N, we have:

Φe_i(N, v~L) = Φe_Sr[i](N, v~L)− X j∈sr(i)

Φe_Sr[j](N, v~L)

= α(Sr[i])−

X

j∈sr(i)

α(Sr[j]).

Thus, each agent’s payoff is equal to his contribution to the egalitarian remainder when he joins all his subordinates.

As we will see below, our solution satisfies several natural principles such as two deletion link principles, a consistency principle, and an amalgamation principle. The rest of the article is devoted to the axiomatic study of the sequential equal surplus division. We provide two alternative characterizations of it on the class C0.

5

Properties for resolving water disputes

In this section, we define some properties of allocation rules Φ on the class C0. The first

prop-erty states that the allocation rule should coincide with the standard solution if the sharing river TU-game involves only two agents.

Standardness (S) For each (N, v~L_{) ∈ C}

0 and each C ∈ N/L such that C = {1,2}, it holds

that:

∀i∈ {1,2}, Φi(N, v ~

L_{) = v}~L_{({i}) +} v ~

L_({1,2})−v~L_({1})−vL~_({2})

2 .

The principle of the efficiency of the water use is translated into the following property.

Component Efficiency (CE) For each (N, v~L_{)∈ C}

0 and each C ∈N/L, it holds that:

ΦC(N, v ~

L_{) =v}L~_(C).

We consider two deletion link properties of solutions onC0 that measure changes in payoffs

and for each of his successors other than the head of the deleted link is the same. Since these two properties are related to fairness as introduced by Myerson (1977) for graph TU-games, we refer to them as downstream fairness and star fairness respectively.

Consider any TU-game (N, v~L_{) ∈ C}

0, any component C ∈ N/L with root r and any

di-rected link i→j. We denote by (Sr[j], v|~LSr[j])∈ C0 the TU-game induced by Sr[j] and v ~ L_{, i.e.} the player set is Sr[j] ⊆ C, the digraph is described by the induced subtree (Sr[j], ~L(Sr[j])) whose root is j and v~L

|Sr[j] is the subgame ofv ~

L _{induced by S}

r[j]. The interpretation follows: if the connection i →j is broken, then the cooperation between the members of Sr[j] and their superiors in the digraph is no longer possible. Thus, the members of Sr[j] consider the worths they can secure for themselves without the cooperation of agents located upstream to j. We will also consider the subgame ({i}, vL~

|{i}) which describes the situation where agent i removes

all his links.

Downstream Fairness (DF) For each (N, vL~_{)∈ C}

0, eachC ∈N/L with at least two agents

and each i∈C such thatsr(i)6=∅, it holds that:

∀j ∈sr(i), Φi(N, v ~ L_)−Φ

i({i}, v ~ L

|{i}) = ΦSr[j](N, v ~ L_)−Φ

Sr[j](Sr[j], v ~ L

|Sr[j]).

In particular, this property implies that deleting all links incident to player i yields the same total change in payoff for each coalition consisting of a successor of i and all his subordinates,

i.e.

∀j, k ∈sr(i), ΦSr[j](N, v ~ L_)−Φ

Sr[j](Sr[j], v ~ L

|Sr[j]) = ΦSr[k](N, v ~ L_)−Φ

Sr[k](Sr[k], v ~ L

|Sr[k]).

Downstream fairness has the flavor of (weighted) Component Fairness (CF) introduced by Her-ings et al. (2008) and B´eal et al. (2012) respectively and applied to river TU-games by van den Brink et al. (2012). Component fairness states that deleting a link between two players in a forest yields the same average change in payoff in the two new components that result from deleting the link. The subtree (Sr[j], ~L(Sr[j])) is the new component containing agent j when the directed link i → j is deleted. Nevertheless, DF differs from CF in three respects: DF is concerned with the total change in payoff in Sr[j] and not with the average change in payoff in

Sr[j]; DF evaluates changes in payoffs when an agent deletes all his links simultaneously and not sequentially; DF takes into account the direction of the river’s flow since the total change in payoff in the set containing i’s superiors is not described.

In order to define the second property of fairness we need the notion of outward-pointing star. Consider a component C ∈N/L. We say that (C, ~L(C)) is an outward-pointing star with root r∈C if L~(C) ={(r, i) :i∈C\ {r}}.

Star Fairness (SF) For each (N, v~L_{) ∈ C}

0, each C ∈ N/L such that |C| ≥ 3 and (C, ~L(C))

is an outward-pointing star with root r∈C, and each directed link r→i, i∈C\{r}, it holds that:

∀j, k∈C\{i}, Φj(N, v ~ L_)−Φ

j(C\{i}, v ~ L

|C\{i}) = Φk(N, v ~ L_)−Φ

k(C,\{i}, v ~ L

|C\{i}).

pointing stars with at least three members. Otherwise, we can apply S if the outward-pointing star contains two members and CE if it is a singleton.

The next property incorporates a consistency principle. Informally, a consistency principle states the following. Fix a solution for a class of TU-games. Assume that some agents leave the game with their payoffs and examine the reduced problem that the remaining agents face. The solution is consistent if for this reduced game, there is no need to re-evaluate the payoffs of the remaining agents. As noted by Thomson (2011), the consistency principle has been examined in the context of a great variety of concrete problems of resource allocation. Since our TU-game is endowed with rooted trees, it is natural to limit our attention to the coalitions formed by an agent and his subordinates.

Pick any digraph TU-game (N, vL~_{)∈ C}

0, anyC ∈N/Lwith rootr ∈C and i∈N. Assume

that the payoffs have been distributed according to the payoff vector z ∈ Rn _{and that the}

players C\Sr[i] leaves the game with their component of the vector z. Let us re-evaluate the situation of Sr[i] at this point. To do this we define the reduced game they face. The worths of coalitions in the reduced games depend on (i) the worths that these coalitions could earn on their own in the original game, (ii) what these coalitions could earn with the leaving players and (iii) the payoff with which the leaving player left the game. Our reduced digraph TU-game (Sr[i], vLz,i~ )∈ C0 induced bySr[i] and z is defined as follows: vz,i~L(Sr[i]) = v~L(C)−zC\Sr[i]

and for each other coalition S ⊂ Sr[i], vLz,i~ (S) = v ~

L_{(S). Thus, v}~L

z,i(Sr[i]) is the total worth left for the remaining agents who interact according to (Sr[i], vz,i~L) on the induced rooted tree (Sr[i], ~L(Sr[i])). Note that for a superadditive digraph game, its reduction is not necessarily su-peradditive. This depends on the worthvL~_(C)−z

C\Sr[i]. If we consider Φ

e _{to define the reduced}

digraph TU-games, then each (Sr[i], vΦL~e_,i) remains superadditive by point (ii) of Proposition 1.

Consequently, if the underlying digraph TU-game is superadditive, as for the river TU-games, we can restrict the analysis to allocations z that preserve this superadditivity property. In this way, the following consistency property can be applied to the class of all superadditive digraph TU-games.

Downstream Consistency (DC) For each (N, vL~_{) ∈ C}

0, each C ∈ N/L and each i ∈ C, it

holds that:

∀j ∈Sr[i], Φj(N, v ~ L_{) = Φ}

j(Sr[i], v ~ L

Φ,i).

DC is a robustness requirement guaranteeing that a coalition of subordinates respect the rec-ommendations made by Φ when the other agents have already received their payoffs according to the solution Φ.

The last property incorporates an amalgamation principle. This principle says something about the changes in payoffs when two or more agents are amalgamated to act as if they were a single agent. It states that if a set of agents are amalgamated into one agent, then the payoff of this agent in the new game coincides with the sum of the payoffs of the amalgamated agents in the original game. This principle has been used by Lehrer (1988), Albizuri (2001) and Albizuri, Aurrekoetxea (2006) in order to characterize various Banzhaf-Coleman indexes. Applying this idea to digraph TU-games we only allow sets of subordinates to be amalgamated.

Pick any digraph TU-game (N, vL~_{)∈ C}

0, anyC ∈N/L with rootr∈C and i∈C. Assume

that i’s subordinates are amalgamated in a way that respects the direction of the river’s flow. Precisely, for each j ∈sr(i), the members of Sr[j] are amalgamated into one player denoted by

player set Ni _{is given by:}

Ni =

N\

[

Sr[j], j ∈sr(i)

[

Sr[j], j ∈sr(i) .

The rooted tree ~Li on Ni contains the directed links i → Sr[j] for each j ∈ sr(i) plus all the original directed links between pairs of agents that belong either to a component other than

C or to C\ S

Sr[j], j ∈ sr(i) . Since the members of Sr[j] behave as a single player, the coalitions contained in Sr[j] as well as their links are not taken into account in the description of the new coalition function. Therefore, we define (Ni_{, v}L~i)∈ C

0 as follows: for each S ∈2N

i

,

vL~i_{(S) =}



    

    

vL~_{(S) if S∩S}

r[j] =∅, and j ∈sr(i),

vL~

S\

Sr[j] :j ∈sr(i) SSr[j] :j ∈sr(i), Sr[j]∈S

otherwise.

In particular, for each playerSr[j], we havevL~i({Sr[j]}) =vL~(Sr[j]).Of course, ifsr(i) is empty, then (Ni_{, v}L~i) coincides with (N, v~L).

Downstream Amalgamation (DA) For each (N, v~L_{) ∈ C}

0, each C ∈ N/L with root r ∈ C

and each i∈C such thatsr(i)6=∅, it holds that:

∀j ∈sr(i), ΦSr[j](N, v ~ L_{) = Φ}

Sr[j](N i_{, v}L~i_).

A similar principle has been used in Ansink and Weikard (2012) in the context of a river shaped like a line. But, these authors depart from the TU-game approach by assuming that each agent along the river has a claim to the river’s flow and that the sum of downstream claims exceeds the sum of downstream endowments at each location. They transform the full problem into an ordered list of two-agent interdependent river sharing problems, each of which is formally equivalent to a bankruptcy problem and is solved through a bankruptcy rule.

van den Brink (2009) also considers the possibility that neighbors collude in a digraph TU-game. His approach is closer to the idea developed by Haller (1994). Here, collusion describes a situation where an agent, say i, becomes a proxy for another agent j, in the sense that j

does not contribute anything to any coalition that does not contain i, and when i enters it is as if i and j enter together. So, the new digraph TU-game contains the same player set than the original game whereas the number of players is smaller when some of them have been amalgamated in our sense. The property defined by Haller (1994) and generalized by van den Brink (2009) to graph TU-game states that the sum of the payoffs distributed to two neighbors in the graph should not change when they collude in their sense. This collusion neutrality property is used to characterize the hierarchical outcome defined in (6).

6

Two characterizations of

_Φ

Proposition 2 The allocation rule Φe _{satisfies S, CE, DF, SF, DC and DA onC}

0.

Proof. From (4) and (5), it is easily verified that Φe _{satisfies S on C}

0. The fact that Φe

satisfies CE on C0 follows directly from part (i) in Proposition 1 and (4). To verify that Φe

satisfies DF, pick any digraph TU-game (N, v~L_{), any component C ∈ N/L with root r ∈ C} and any agent i∈C such that sr(i)6=∅. For each j ∈sr(i), we have:

Φe

Sr[j](N, v ~ L_)−Φe

Sr[j](Sr[j], v ~ L

|Sr[j]) = Φ e

Sr[j](N, v ~

L_)−vL~_(S r[j]) =α(Sr[j])−v

~ L_(S

r[j]) = 1

|sr[i]|

α(Sr[i])−

X

k∈sr(i)

v~L(Sr[k])−v ~ L_({i})

= Φe i(N, v

~

L_)−vL~_({i}) = Φe

{i}(N, v

~ L_)−Φe

{i}({i}, v

~ L

|{i}),

where first equality follows from the fact that Φe_{satisfies CE onC}

0. The second equality follows

from part (i) in Proposition 1. The third and four equalities come from pr(j) = i and (4)-(5) respectively. Therefore, Φe _{satisfies DF on C}

0.

Next, consider a situation where the digraph TU-game (N, v~L_{)∈ C}

0 possesses a component

C ∈N/L containing at least three agents and shaped like an outward-pointing star with root

r ∈ C. Pick any directed link r → i. In order to verify that Φe _{satisfies SF, we first compute} Φe

j(N, v ~

L_{) for each j ∈ C. By construction and definition of the egalitarian remainder, we}

have: Sr[r] = C, α(C) = vL~(C) and for each j ∈ C\{r}, pr(j) = r and also Sr[j] = {j}. Consequently, from (4) and (5) we get:

∀j ∈C, Φe_j(N, vL~) =vL~({j}) + 1 |C|

v~L(C)−X k∈C

v~L({k})

. (7)

By a similar computation on the subgame (C\{i}, vL~

|C\{i}), we get that for each j ∈C\{i}:

Φe_j(C\{i}, v_|~L_C\{i}) =vL_|~_C\{i}({j}) + 1 |C| −1

v_|L~_C\{i}(C\{i})− X k∈C\{i}

v_|L~_C\{i}({k})

. (8)

From (7)-(8) and the fact that vL~_{({j}) =v}L~

|C\{i}({j}) for each j ∈C\{i}, we get:

∀j, k ∈C\{i}, Φe_j(N, vL~)−Φe_j(C\{i}, v_|L~_C\{i}) = Φe_k(N, v~L)−Φe_k(C\{i}, v_|~L_C\{i}),

which proves that Φe _{satisfies SF on C}

0.

In order to verify that Φe _{satisfies DC on C}

0, we first compare the payoffs Φei(N, v ~ L_{) and}

Φe

i(Sr[i], vΦ~Le_,i) for any (N, v ~ L_{) ∈ C}

0, any C ∈ N/L and i ∈ C. By definition of (Sr[i], vLΦ~e_,i),

we have vL~

Φe_,i(Sr[i]) = v~L(C)− ΦC\Sr[i](N, v ~

L_{). Because Φ}e _{satisfies CE and by part (i) of}

Proposition 1, we get:

v_ΦL~e_,i(S_r[i]) = Φ_Sr[i](N, v ~

L_{) =α(S} r[i]).

Φe_i(Sr[i], v ~ L

Φe_,i) = v ~ L

Φe_,i({i}) +

1 |sr[i]|



v

~ L

Φe_,i(S_r[i])−

X

j∈sr(i)

vL_Φ~e_,i(S_r[j])−v ~ L

Φe_,i({i})





= vL~({i}) + 1 |sr[i]|



α(Sr[i])−

X

j∈sr(i)

v~L(Sr[j])−v ~ L_({i})





= Φe_i(N, vL~),

as desired for player i. From this, we deduce that the egalitarian remainder for each j ∈sr(i) is the same in (Sr[i], vΦL~e_,i) and (N, v

~

L_{). So, using the definition of (S}

r[i], vLΦ~e_,i), we also have

Φe

j(Sr[i], vΦL~e_,i) = Φe_i(N, v ~

L_{) for each j ∈s}

r(i). Continuing in this fashion for each subordinate of i, we reach the desired conclusion.

Finally, consider any digraph TU-game (N, vL~_{)∈ C}

0, any component C ∈N\L, any i∈C

such that sr(i)6=∅. Pick anyj ∈sr(i). On the one hand, by part (i) of Proposition 1, we have Φe

Sr[j](N, v ~

L_{) = α(S}

r[j]). On the other hand, from (5) and definition of the digraph TU-game (Ni_{, v}L~i), we deduce that Φe

k(Ni, v ~

Li) = Φe k(N, v

~

L_{) for each player k who does not belong to} the set of i’s subordinates. To understand this equality, note that the egalitarian remainder for such ak in (N, vL~_{) and Φ}e

k(N, v ~

L_{) do not rely on proper coalitions of S}

r[j],j ∈sr(i) so that the computations from v~L _{give the same results as the computations from v}L~i. Therefore, for each

j ∈sr(i), the egalitarian remainder forSr[j] in (N, vL~) coincides with the egalitarian remainder forSr[j] in (Ni, vL~i).Because each playerSr[j],j ∈sr(i), has no successor in (Ni, ~Li), we easily conclude that Φe

Sr[j](N

i_{, v}L~i) =α(S

r[j]) = Φe_Sr[j](N, vL~). This proves that Φe satisfies DA in C0.

Combining CE and DF we obtain a characterization of the sequential equal surplus division on C0.

Proposition 3 The sequential equal surplus division Φe _{is the unique allocation rule that}

satisfies CE and DF on C0.

Proof. By Proposition 2, Φe _{satisfies CE and DF. Next, consider an allocation rule Φ that} satisfies CE and DF on C0. To show: Φe = Φ on C0. Pick any digraph TU-game (N, vL~) and

any C ∈N/L. First note that, for each i∈C, we have:

Φ_i(N, vL~) = Φ_Sr[i](N, v~L)− X j∈sr(i)

Φ_Sr[j](N, vL~).

It remains to prove that, for each i ∈ C, Φ_Sr[i](N, vL~_{) is uniquely determined by CE and DF.} We proceed by induction on the depth q of the agents in (C, ~L(C)).

Initial step_{: If q= 0, then i=r. By CE, we get:}

Φ_Sr[r](N, v~L) = Φ_C(N, v~L) =v(C).

Induction hypothesis_{: Assume that the assertion is true for eachi∈C such that his depth}

is inferior or equal to q < dC where dC is the depth of the rooted tree (C, ~L(C)).

Induction step_{: Pick any i∈C such that his depth is equal to q+ 1. By DF, we have:}

Φ_pr(i)(N, v~L)−vL~({pr(i)}) = ΦSr[i](N, v ~

L_)−v~L_(S r[i]). Denote this quantity by δ. By DF and CE, we obtain:

∀j ∈sr(pr(i)), ΦSr[j](N, v ~

L_{) =v}L~_(S

r[j]) +δ. We also have:

Φ_pr(i)(N, v~L) =v~L({pr(i)}) +δ. Summing all these equalities, we get:

Φ_Sr[pr(i)](N, vL~) = X j∈sr[pr(i)]

vL~(Sr[j]) +|sr[pr(i)]|δ.

By the induction hypothesis, Φ_Sr[pr(i)](N, vL~_{) is uniquely determined. As a consequence, the} parameter δ is uniquely determined. This gives the result for player i since Φ_Sr[i](N, vL~_{) =}

vL~_(S

r[i]) +δ.

The next proposition provides an alternative characterization of the sequential equal surplus division.

Proposition 4 The sequential equal surplus division Φe _{is the unique allocation rule that}

satisfies CE, S, SF, DC and DA on C0.

In order to prove the above statement, we need an intermediary result establishing that if an allocation rule satisfies CE, S and SF on the class of outward-pointing star TU-games, i.e.

situations in which the rooted trees are shaped like outward-pointing stars, then it coincides with Φe_.

Lemma 1 If an allocation rule Φ satisfies CE, S and SF on C0, then for each (N, vL~) ∈ C0

and each C ∈ N/L such that ~L(C) is shaped like an outward-pointing star, it holds that

Φ_j(N, vL~_{) = Φ}e j(N, v

~

L_{)for each j ∈C.}

Proof. By Proposition 2, Φe _{satisfies CE, S and SF on C}

0. Consider any allocation rule Φ

that satisfies CE, S and SF on C0 and pick any (N, vL~)∈ C0 such that there isC∈N/L where

~

L(C) is shaped like an outward-pointing star with rootr ∈C. We proceed by induction on the number of elements of C.

Initial step_{: If C ={j} for some j ∈N, then by CE, Φ}

j(N, v ~

L_{) = Φ}e j(N, v

~

L_{). If C ={i, j},}

then by S, Φi(N, v ~

L_{) = Φ}e i(N, v

~

L_{) and Φ} j(N, v

~

L_{) = Φ}e j(N, v

~ L_).

Induction hypothesis_{: Assume that the statement is true forCwith at mostq∈}N_elements.

Induction step_{: Assume that C contains q+ 1 elements and delete the directed link r → i}

for some i∈C\{r}. By DF and the induction hypothesis we have:

∀j, k ∈C\{i}, Φj(N, v ~ L_)−Φ

k(N, v ~

L_{) = Φ}

j(C\{i}, v ~ L

|C\{i})−Φk(C,\{i}, v ~ L

|C\{i})

= Φe_j(C\{i}, v_|L~_C\{i})−Φe_k(C,\{i}, vL_|~_C\{i})

Thus there is a constant c∈R _{such that:}

∀j ∈C\{i}, Φj(N, v ~ L_)−Φe

j(N, v ~ L_{) = c.}

Because these equalities remain valid whatever the chosen deleted link, we have:

∀j ∈C, Φj(N, v ~ L_)−Φe

j(N, v ~ L_{) = c.}

By CE, ΦC(N, v ~

L_{) = Φ}e C(N, v

~

L_{) = v(C) and so c = 0. This shows that, for each j ∈ C,}

Φj(N, vL~) = Φej(N, v ~

L_).

Proof. (of Proposition 4). By Proposition 2, Φe _{satisfies CE, S, SF, DC and DA on C}

0.

Next, pick any allocation rule Φ that satisfies CE, S, SF, DC and DA on C0 and consider any

(N, vL~_{) ∈ C}

0 and any C ∈ N/L. To show: for each i ∈ C, Φi(N, vL~) is uniquely determined. We proceed by induction on the depth of the subtree (C, ~L(C)) rooted at r ∈C.

Initial step_{: Assume that the depth of the rooted tree (C, ~L(C)) is equal to zero or one. In}

such case, the rooted tree is shaped like an outward pointing star. By Lemma 1, the payoffs (Φi(N, v~L))i∈C are uniquely determined.

Induction hypothesis_{: Assume that the payoffs (Φi(N, v}L~_{))i∈C are uniquely determined for}

each (C, ~L(C)) whose depth is dC <|C| −1.

Induction step_{: Assume that the depth of (C, ~L(C)) is dC + 1 > 1. From (N, v}L~_{) and r,}

construct the digraph TU-game (Nr_{, v}L~r) where player r’s subordinates are amalgamated. By

construction,r is now the root of an outward-pointing star in the corresponding component of (Nr_{, ~L}

r), i.e. we have r → Sr[j] for each j ∈sr(r). Since by assumption there is at least one agent with no successor whose depth is strictly greater than one, (Nr_{, v}L~r_{) does not coincide}

with (N , vL~_{). By Lemma 1, for eachj ∈s}

r(r), the payoff Φ_Sr[j](Nr, v~Lr) is uniquely determined. By DA, we get:

∀j ∈sr(r), Φ_Sr[j](Nr, v ~

Lr_{) = Φ}

Sr[j](N , v ~ L_),

which means that the total payoff of each coalition Sr[j], j ∈sr(r), is uniquely determined in the original game (N, v~L_{). Using CE, we obtain that agent r’s payoff is uniquely determined in} (N , v~L_):

Φr(N , v ~

L_{) =v}L~_(C)− X

j∈sr(r)

ΦSr[j](N , v ~ L_).

It remains to show that the payoff of each other agent in the component is uniquely determined. Consider any j ∈sr(r) and construct the reduced digraph TU-game (Sr[j], vΦ~L,j). By definition of the reduced digraph TU-game, we have:

∀S ⊂Sr[j], v ~ L

Φ,j(S) =v ~

L_{(S) and v}L~

Φ,j(Sr[j]) =v ~

L_(C)−Φ

C\Sr[j](N , v ~ L_).

Note that ΦC\Sr[j](N , v ~

L_{) is uniquely determined by the previous step so that (S} r[j], v

~ L

Φ,j) is well defined. By construction, the depth of each directed subtree (Sr[j], ~L(Sr[j])), j ∈ sr(r), is at most dC. By the induction hypothesis, for each j ∈ sr(r) and i ∈ Sr[j], Φi(Sr[j], vLΦ~,j) is uniquely determined. By DC we get:

∀j ∈sr(r),∀i∈sr(j), Φi(Sr[j], v ~ L

Φ,j) = Φi(N, v ~ L_),

which means that the payoff of each subordinate of r is uniquely determined in (N, v~L_{). This}