Edge pair sum labeling of some cycle related graphs

(1)

journal homepage: http://jac.ut.ac.ir

Edge pair sum labeling of some cycle related graphs

P. Jeyanthi

∗1

and T.Saratha Devi

†2

1_{Govindammal Aditanar College for Women Tiruchendur-628 215, Tamil Nadu, India.}

2_{Department of Mathematics, G.Venkataswamy Naidu College,}

Kovilpatti-628502,Tamilnadu,India.

ABSTRACT ARTICLE INFO

Let G be a (p,q) graph. An injective map f :E(G) → {±1,±2,· · · ,±q}is said to be an edge pair sum labeling if the induced vertex function f∗ :V(G)→Z− {0} de-fined by f∗(v) = P

eEv

f(e) is one-one where Ev denotes

the set of edges inGthat are incident with a vertexv and

f∗(V(G)) is either of the form n

±k1,±k2,· · · ,±kp

2

o

orn±k1,±k2,· · · ,±kp−1 2

o Sn_±

kp+1 2

o

according as p is even or odd. A graph with an edge pair sum labeling is called an edge pair sum graph. In this paper we prove that the graphs GL(n), double triangular snake D(Tn),

Wn, F ln, hCm, K1,ni and hCm∗K1,ni admit edge pair

sum labeling.

Article history:

Received 28, January 2016 Received in revised form 9, September 2016

Accepted 30 October 2016 Available online 01, November 2016

Keyword: Edge pair sum labeling, edge pair sum graph,double triangular snake,wheel graph,flower graph

AMS subject Classification: 05C78.

1 Introduction

Throughout this paper we consider finite, simple and undirected graphG= (V(G), E(G)) with pvertices and q edges. Gis also called a (p, q) graph. We follow the basic notations

∗_{Corresponding author: P. Jeyanthi. Email: jeyajeyanthi@rediffmail.com} †_{rajanvino03@gmail.com}

(2)

and terminologies of graph theory as in [2]. A graph labeling is an assignment of integers to the vertices or edges or both, subject to certain conditions. There are several types of labeling and for a dynamic survey of various graph labeling problems along with extensive bibliography we refer to Gallian [1]. Ponraj and Parthipan introduced the concept of pair sum labeling in [12]. An injective mapf :V(G)→ {±1,±2, . . . ,±p} is said to be a pair sum labeling of a graphG(p, q) if the induced edge functionfe:E(G)→Z− {0} defined

byfe(uv) =f(u)+f(v) is one-one andfe(E(G)) is either of the form

n

±k1,±k2, . . . ,±kq₂

o

orn±k1,±k2, . . . ,±kq−1 2

o

∪n±kq+1 2

o

according as q is even or odd. A graph with a pair sum labeling, it is called a pair sum graph. Analogous to pair sum labeling we defined a new labeling called edge pair sum labeling [3] and further studied in [4-10]. In this paper we prove that the graphsGL(n), double triangular snakeD(Tn),Wn,F ln,hCm, K1,niand hCm∗K1,ni admit edge pair sum labeling.

We use the following definitions in the subsequent sequel.

Definition 1. A complete bipartite graph is a simple bipartite graph such that two vertices are adjacent if and only if they are in different partite sets. If partite sets V1 and V2 are

having m and n vertices respectively then the related complete bipartite graph is denoted by Km,n and V1 is called m-vertices part and V2 is called n-vertices part of Km,n.

Definition 2. The double triangular snake D(Tn) is the graph obtained from the path

u1, u2, u3, ..., un by joining ui andui+1 with two new vertices vi andwi for1≤i≤(n−1).

Definition 3. The wheel graphWn is the joining of the graphs Cn and K1 that is, Wn =

Cn+K1. Here the vertices corresponding to Cn are called rim vertices and Cn is called

rim of Wn while the vertex corresponds to K1 is called apex vertex.

Definition 4. A helm Hn n ≥ 3 is the graph obtained from the wheel Wn by adding a

pendant edge at each vertex on the wheels’s rim.

Definition 5. The flower graph F lnis the graph obtained from a helm Hn by joining each

pendant vertex to the apex of the helm.

Definition 6. The graphhCm, K1,niis the graph obtained fromCm andK1,nby identifying

any one of the vertices of Cm with the central vertex of K1,n [11].

Definition 7. The graph hCm∗K1,ni is the graph obtained from Cm and K1,n by

identi-fying any one of the vertices of Cm with a pendant vertex of K1,n (that is a non-central

vertex of K1,n)[11].

2 Preliminary Results

(3)

• Every pathPn is an edge pair sum graph for n≥3. • Every cycle Cn (n ≥3) is an edge pair sum graph.

• The star graph K1,n is an edge pair sum graph if and only if n is even. • The complete graph K4 is not an edge pair sum graph.

3 Main Results

Theorem 1. The complete bipartite graph K2,n is an edge pair sum graph.

Proof. Define V(K2,n) = {u, v, ui : 1 ≤ i ≤ 2n} and E(K2,n) = {ei = uui, e

0

i = vui :

1 ≤ i ≤ 2n} are the vertices and edges of the graph K2,n. Define the edge labeling

f : E(K2,n) → {±1,±2,±3, ...,±4n}. For 1 ≤ i ≤ 2n f(ei) = i and f(e

0

i) = −(2n−

i+ 1). Then the induced vertex labeling is as follows: For 1 ≤ i ≤ n f∗(ui) = −(2n−

2i+ 1) and f∗(un+i) = 2i − 1, f∗(u) = n(2n + 1) = −f∗(v). Then f∗(V(K2,n)) = {±1,±3,±5, ...,±(2n −1),±(2n2 ₊_n₎_}_{. Hence} _f _{is an edge pair sum labeling for all}

n. The example for the edge pair sum graph labeling of K2,2 is shown in Figure 1.

t t t t

t t

1 2 3

4

-4 _-3 _-2

-1

Figure 1: Edge pair sum labeling for the graph K2,2

Theorem 2. The double triangular snake D(Tn) is an edge pair sum graph.

Proof. Let G(V, E) = D(Tn). Then V(G) = {ui : 1 ≤ i ≤ n, vi, wi : 1 ≤ i ≤ (n−1)}

and E(G) = {e2i−1 = uivi, e2i =u1+ivi, e

0

2i−1 = uiwi, e

0

2i = u1+iwi, e

00

i = uiu1+i : 1 ≤ i ≤

(n−1)} are the vertices and edges of the graph G. Define the edge labeling f :E(G)→ {±1,±2,±3, ...,±(5n−5)} by considering the following two cases.

Case(i). n is even. Subcase (a). n= 4.

Define f(e00₁) = −2, f(e00₂) = −1, f(e₃00) = 3, for 1 ≤ i ≤(n−1) f(e2i−1) = n−2 + 2i = −f(e0₂_i₋₁) and f(e2i) = n−1 + 2i = −f(e

0

2i). The induced vertex labeling is as follows:

f∗(u1) =−2 =−f∗(u3),f∗(u2) = −3 = −f∗(u4) and for 1≤i≤(n−1)f∗(vi) = 2n−3+

4i=−f∗(wi). Then f∗(V(G)) ={±2,±3,±(2n+ 1),±(2n+ 5),±(2n+ 9), ...,±(6n−7)}.

(4)

For 1≤i≤(n−1) f(e2i−1) =n−2 + 2i=−f(e

0

2i−1) and f(e2i) =n−1 + 2i=−f(e

0

2i),

for 1 ≤ i ≤ n

2 −2 f(e

00

i) = n+ 1 −2i, f(en2−1) = −2, f(e

n

2) = −1, f(e

n

2+1) = 3 and

for n₂ + 2 ≤ i ≤ (n−1) f(e00_i) = n−1−2i. The induced vertex labeling is as follows: for 1 ≤ i ≤ (n −1) f∗(vi) = 2n−3 + 4i = −f∗(wi), f∗(u1) = n −1 = −f∗(un), for

2 ≤ i ≤ n

2 −2 f

∗₍_u

i) = 2(n + 2−2i), f∗(un

2−1) = 3 = −f

∗₍_u_n

2), f

∗₍_u_n

2+1) = 2 =

−f∗(un

2+2) and for (

n

2 + 3) ≤ i ≤ (n−1) f

∗₍_u

i) = 2(n−2i). Then we get f∗(V(G)) = {±2,±3,±12,±16,±20, ...,±(2n−4),±(n−1),±(2n+1),±(2n+5),±(2n+9), ...,±(6n−

7)}. Hence f is an edge pair sum labeling. The example for the edge pair sum graph labeling of D(T6) is shown in Figure 2.

t t t t t t

t t t t t

5 -2 -1 3 -5

6 7 8 ₉ 10 ₁₁12 ₁₃₁₄ 15

-15

-6 -7 -8 -9 -10

-11

-12 -13 -14

Figure 2: Edge pair sum labeling for the graph D(T6)

Case(ii). n is odd. Subcase (a). n= 3.

Define f(e00₁) = −2, f(e00₂) = 1, for 1 ≤ i ≤ (n−1) f(e2i−1) = 2i+ 1 = −f(e

0

2i−1) and

f(e2i) = 2i+ 2 = −f(e

0

2i). The induced vertex labeling is as follows: f∗(u1) = −2,

f∗(u2) = −1 = −f∗(u3) and for 1 ≤ i ≤ (n −1) f∗(vi) = 4i+ 3 = −f∗(wi). Then

f∗(V(G)) = {±1,±7,±11,±15, ...,±(4n − 1)}S

{−2}. Hence f is an edge pair sum labeling for n= 3.

Subcase (b). n >3.

For 1≤i≤(n−1) f(e2i−1) =n−1 + 2i=−f(e

0

2i−1) and f(e2i) = n+ 2i=−f(e

0

2i), for

1≤ i≤ n−3 2 f(e

00

i) =−(n+ 2−2i), f(e

00

n+1 2

) = 1, f(e00n−1 2

) = 2 and for n+3₂ ≤i ≤(n−1)

f(e00_i) = −n+ 2 + 2i. The induced vertex labeling is as follows: for 1 ≤ i ≤ (n −1)

f∗(vi) = 2n−1 + 4i = −f∗(wi), f∗(u1) = −n = −f∗(un), for 2 ≤ i ≤ n−₂3 f∗(ui) =

2(−n−3 + 2i), f∗(un−1

2 ) = −3 = −f

∗₍_u

n+1 2 ), f

∗₍_u

n+3

2 ) = 6 and for (

n+5

2 ) ≤ i ≤ (n−

1) f∗(ui) = −2(n−1−2i). Then we get f∗(V(G)) = {±3,±12,±16,±20, ...,±(2n−

2),±n,±(2n+ 3),±(2n+ 7),±(2n+ 11), ...,±(6n−5)}S

{6}. Hence f is an edge pair sum labeling. The example for the edge pair sum graph labeling of D(T5) is shown in

Figure 3.

Theorem 3. The wheel graph Wn is an edge pair sum graph.

Proof. Let V(Wn) = {v, ui : 1 ≤ i ≤ n} and E(Wn) = {e

0

i = vui : 1 ≤ i ≤ n, e1 =

(5)

t t _t _t _t

t t t t

J J

-5 2 1 5

6 7 ₈ 9 ₁₀ 11 ₁₂ ₁₃

t t t t

T T

-7 -9

-6 -8 -10 -11 -12 -13

Figure 3: Edge pair sum labeling for the graph D(T5)

the edge labeling f : E(Wn) → {±1,±2,±3, ...,±2n} by considering the following two

cases.

Case(i). n is even. For 1≤i≤ n

2 f(ei) =iand f(en2+i) =−(

n

2 + 1−i), for 1≤i≤( n

2−1)f(e

0

i) =n+ 2 + 2i

and f(e0n

2+i) =−2(n+ 1−i), f(e

0

n

2) =−(n+ 2) and f(e

0

n) = ( n

2 + 1). Then the induced

vertex labeling is as follows: for 1 ≤ i ≤ (n₂ −1) f∗(ui) = n + 3 + 4i and f∗(un₂+i) = −(3n+ 3−4i), f∗(un

2) = −(n+ 2) and f

∗₍_u

n) = (n₂ + 1) = −f∗(v). Therefore we get

f∗(V(Wn)) = {±(n₂ + 1),±(n+ 7),±(n + 11),±(n + 15), ...,±(3n −1)}S{−(n + 2)}.

Hence f is an edge pair sum labeling. The examples for the edge pair sum graph labeling of W4 and W8 are shown in Figure 4.

t

t t

tt t

t tt

t

t t

1

2

-2 -1

3

8

-8

1 2

3

4

-4 -3

-1 12 14

16

-10 -16 -14 -12

-5

-6 -2

Figure 4: Edge pair sum labeling for the graph W4 and W8

(6)

Subcase (a). n= 1,2(mod3).

Definef(e1) = 1, f(e2) =−2, for 1≤i≤(n−₂3)f(e2+i) = 2 +i=−f(en+3

2 +i),f(e

n+3 2 ) =

−1, f(e0₁) = n −1 = −f(e0₂), for 1 ≤ i ≤ (n−₂5) f(e0₂₊_i) = n −1 + 2i = −f(e0n+3 2 +i

),

f(e0n+1 2

) = 2n−5 =−f(e0_n) and f(e0n+3 2

) = 2. Then the induced vertex labeling is as

fol-lows: f∗(u1) =n−2 =−f∗(u2), for 1 ≤i≤(n−₂5) f∗(u2+i) =n+ 4 + 4i=−f∗(un+3 2 +i),

f∗(un+1 2 ) =

5n−11 2 =−f

∗₍_u

n) and f∗(un+3

2 ) = −2 =f

∗₍_v_{). Then}

f∗(V(Wn)) = {±2,±(5n−₂11),±(n− 2),±(n + 8),±(n + 12),±(n+ 16), ...,±(3n −6)}.

Hence f is an edge pair sum labeling. Subcase (b). n= 0(mod3).

Definef(e1) = 3, f(e2) = 4, f(e3) = −5, for 1≤i≤(n−₂5) f(e3+i) = 5 +i=−f(en+5 2 +i),

f(en+3

2 ) =−3,f(e

n+5

2 ) =−4, f(e

0

1) =−(n+ 1), f(e

0

2) =−1 =−f(e

0

3), for 1≤i≤( n−3

2 )

f(e0₃₊_i) = n+5₂ +i, f(e0n+5 2

) = 5 and for 1 ≤ i ≤ (n−₂5) f(e0n+5 2 +i

) = −(n+5₂ +i) . Then the induced vertex labeling is as follows: f∗(u1) = −(n− 6) = −f∗(un+3

2 ), f

∗₍_u

2) = −2 = −f∗(u3), for 1 ≤ i ≤ (n−₂7) f∗(u3+i) = n+5₂ + 11 + 3i = −f∗(un+5

2 +i), f

∗₍_u

n+1 2 ) =

3n−1

2 = −f

∗₍_u

n) and f∗(un+5

2 ) = −5 = f

∗₍_v_). _Then _f∗₍_V₍_W

n)) = {±2,±5,±(n −

6),±(3n₂−1),±(n+33₂ ),±(n+39₂ ),±(n+45₂ ), ...,±(2n+ 3)}. Hence f is an edge pair sum la-beling. The examples for the edge pair sum graph labeling of W7 and W9 are shown in

Figure 5. t t t t t t t t t t t t t t t t t t 1 -2 3 4 -1 -3 -4 -9 6 -6 8 9 2 -8 3 ₄ -5 6 7 -3 -4 -6 -7 -8 -9 -10 -1 1 8 9 10 5

Figure 5: Edge pair sum labeling for the graph W7 and W9

Theorem 4. The flower graph F ln is an edge pair sum graph.

Proof. LetV(F ln) ={w, ui, vi : 1≤i≤n}and E(F ln) ={e1 =unu1, e1+i =uiu1+i : 1≤

i ≤ (n−1), e0_i = wui, e

00

i = uivi, e

000

i = wvi : 1≤ i ≤ n} are the vertices and edges of the

graph F ln. Define the edge labeling f :E(F ln) → {±1,±2,±3, ...,±4n} by considering

(7)

Case(i). n is odd.

For 1 ≤ i ≤ (n+1₂ ) f(e2i−1) = −(4i −2), for 1 ≤ i ≤ (n−₂1) f(e2i) = −(2n + 4i) ,

for 1 ≤ i ≤ n f(e_i0) = −(2i−1) = −f(e00_i) and f(e_i000) = −(2n− 1 + 2i). Then the induced vertex labeling is as follows: for 1 ≤ i ≤ (n −1) f∗(ui) = −(2n+ 2 + 4i), for

1 ≤ i ≤ n f∗(vi) = 2n −2 + 4i, f∗(un) = −(2n+ 2) and f∗(w) = 2n2. Then we get

f∗(V(F ln)) ={±(2n+2),±(2n+6),±(2n+10),±(2n+14), ...,±(6n−2)}

S

{2n2_}_{. Hence}

f is an edge pair sum labeling for n is odd. The example for the edge pair sum graph labeling of F l5 is shown in Figure 6.

-2

-14

-6

-18 -10

-1

-3

-5 -7

-9

t t

t

t t

t

t t

t

t t

1

3

5 7

9

11

13

15 17

19

Figure 6: Edge pair sum labeling for the graph F l5

Case(ii). n is even. Subcase (a). n= 4. For 1≤i≤ n

2 f(ei) = i=−f(en2+i),f(e

0

i) = 4n−i+1 =−f(e

00

i),f(e

0

n

2+i) = −(

7n+2 2 −i) = −f(e00n

2+i), f(e

000

i ) = −(n2 −1 + 2i) and f(e

000

n

2+i) = n+ 2i−1. Then the induced vertex

labeling is as follows: for 1 ≤ i ≤ n−2 2 f

∗₍_u

i) = 2i+ 1 = −f∗(un₂+i), f∗(un₂) = −1 = −f∗(un), for 1 ≤ i ≤ n₂ f∗(vi) = −1₂(9n + 2i) = −f∗(vn₂+i) and f∗(w) = n

2

2 . Then

f∗(V(F ln)) ={±1,±3,±5,±7, ...,±(n−1),±(9n₂+2),±(9n₂+4),±(9n₂+6), ...,±5n}

S

{n2

2 }.

Hence f is an edge pair sum labeling. Subcase (b). n= 2(mod4).

For 1≤i≤ n

2 f(ei) = i=−f(en2+i),f(e

0

i) = 4n−i+1 =−f(e

00

i),f(e

0

n

2+i) = −(

7n+2 2 −i) = −f(e00n

2+i),f(e

000

i ) =−(n2−1+2i) andf(e

000

n

2+i) = n+2i−1. Then the induced vertex labeling

is as follows: for 1 ≤ i ≤ n−2 2 f

∗₍_u

(8)

for 1 ≤ i ≤ n 2 f

∗₍_v

i) = −1₂(9n+ 2i) = −f∗(vn₂+i) and f∗(w) = n

2

2. Then f

∗₍_V₍_{F l}

n)) = {±(n−₂2),±3,±5,±7, ...,±(n−1),±(9n₂+2),±(9n₂+4),±(9n₂+6), ...,±5n}S

{n2

2 }. Hencef is

an edge pair sum labeling. Subcase (c). n = 0(mod4).

For 1 ≤ i ≤ n

2 f(ei) = i, f(en2+1) = −2, f(e

n

2+2) = −1, for 1 ≤ i ≤

n−4

2 f(en2+2+i) =

f(en

2+i)−2, for 1≤i≤

n 2 f(e

0

i) = 4n−i+ 1 =−f(e

00

i),f(e

0

n

2+i

) = −(7n+2

2 −i) = −f(e

00

n

2

),

f(e000_i ) =−(n

2 + 2i) and f(e

000

n

2+i

) =n+ 2i. Then the induced vertex labeling is as follows: for 1≤i≤(n₂−1)f∗(ui) = 2i+1 =−f∗(un₂+i),f∗(un₂) = n₂−2 = −f∗(un), for 1≤i≤ n₂

f∗(vi) = −1₂(9n+ 2 + 2i) = −f∗(vn₂+i) and f∗(w) = n

2

2 . Then f

∗₍_V₍_{F l}

n)) = {±(n₂ −

2),±3,±5,±7, ...,±(n−1),±(9n₂+4),±(9n₂+6),±(9n+10₂ ), ...,±(5n+ 1)}S

{n2

2 }. Hencef is

an edge pair sum labeling. The example for the edge pair sum graph labeling of F l6 is

shown in Figure 7.

t

t t

t

t t

t

t t

1

2

3

-1

-2 -3

24 23

22

-21 -20

-19

-23 -24

-22

21 20

19

-4

-6

-8

7 9

11

Figure 7: Edge pair sum labeling for the graph F l6

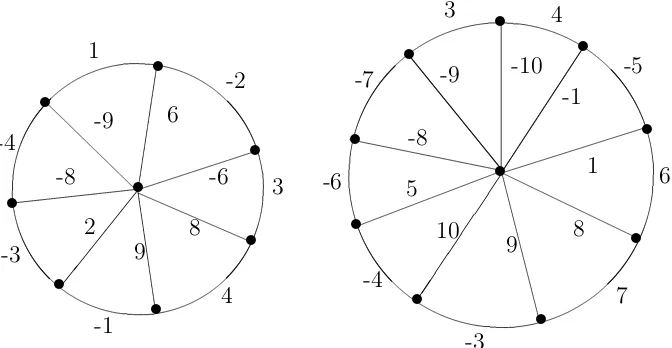
Theorem 5. The graph hCm, K1,ni is an edge pair sum graph for m≥4 and n is odd.

Proof. LetV(hCm, K1,ni)={ui : 1≤i≤m, vi : 1≤i≤n}and

E(hCm, K1,ni)={ei =uiui+1 : 1≤ i≤(m−1), em =umu1, e

0

i =uivi : 1 ≤i≤ n} are the

vertices and edges of the graph hCm, K1,ni. Define the edge labeling f :E(hCm, K1,ni)→ {±1,±2,±3, ...,±(m+n)} by considering the following four cases.

Case(i). m = 4.

Define f(e1) = 2 = −f(e3), f(e2) = −1 = −f(e4), f(e11) = 3 and for 1 ≤ i ≤ n−1

2

f(e0₁₊_i) = 6 +i = −f(e0n+1 2 +i

). The induced vertex labeling is as follows: f∗(u1) = 6,

f∗(u2) = 1 = −f∗(u4), f∗(u3) = −3 = −f∗(v1) and for 1 ≤ i ≤ n−₂1 f∗(v1+i) = 6 +i = −f∗(vn+1

2 +i). Then f

∗₍_V₍_h_C

m, K1,ni)) = {±1,±3,±7,±8,±9, ...,±(n+11₂ )}S{6}. Hence

f is an edge pair sum labeling.

(9)

Define f(e1) =−1 =−f(e3),f(e2) =−3 =−f(e5),f(e4) =−2 =f(e11) and for 1≤i≤ n−1

2 f(e

0

1+i) = 4 +i=−f(e

0

n+1 2 +i

). The induced vertex labeling is as follows: f∗(u1) = 4 =

−f∗(u2),f∗(u3) =−2 = −f∗(v1),f∗(u4) =−1 = −f∗(u5) and for 1≤i≤ n−₂1 f∗(v1+i) =

4 +i = −f∗(vn+1

2 +i). Then f

∗₍_V₍_h_C

m, K1,ni)) = {±1,±2,±4,±5,±6,±7, ...,±(n+7₂ )}.

Hence f is an edge pair sum labeling. The examples for the edge pair sum graph labeling of < C4, K1,3 > and < C5, K1,5 >are shown in Figure 8.

t

t t t

t tt t t t t t t t t t t t 1 2 -1 -2 3 7 -7 3 -1 -3 1 -2 ₂ 5 6 -5 -6

Figure 8: Edge pair sum labeling for the graph < C4, K1,3 > and < C5, K1,5 >

Case(iii). m is even. Subcase (a). m= 2(mod4).

Definef(e1) = m₂ =−f(em+2

2 ), for 1≤i≤

m−2

2 f(e1+i) =−i=−f(em2+2+i),f(e

0

1) = m−1

and for 1 ≤ i≤ n−1 2 f(e

0

1+i) = m−1 + 2i =−f(e

0

n+1 2 +i

). The induced vertex labeling is

as follows: f∗(u1) = 2(m−1), f∗(u2) = m₂−2 =−f∗(um+4

2 ), for 1 ≤ i ≤

m−4 2 f

∗₍_u

2+i) = −2i−1 =−f∗(um+4

2 +i),f

∗₍_u

m+2

2 ) = −m+1 =−f

∗₍_v

1) and for 1≤i≤ n−₂1 f∗(v1+i) =m−

1+2i=−f∗(vn+1

2 +i). Thenf

∗₍_V₍_h_C

m, K1,ni))={±(m−1),±(m₂−2),±3,±5,±7, ...,±(m−

3),±(m+ 1),±(m+ 3),±(m+ 5), ...,±(m+n −2)}S

{2(m−1)}. Hence f is an edge pair sum labeling.

Subcase (b). m= 0(mod4).

Define f(e1) = m₂ = −f(em₂), f(e2) = −2, f(e3) = −1, for 1 ≤ i ≤ m−₂8 f(e3+i) =

f(e1+i)−2,f(em+2

2 ) = −(

m

2 −1) =−f(em), for 1≤i≤ m−4

2 f(em2+2+i) = i,f(e

0

1) = m−1

and for 1≤i≤ n−1 2 f(e

0

1+i) =m−1 + 2i=−f(e

0

n+1 2 +i

). The induced vertex labeling is as

follows: f∗(u1) = 2m−2,f∗(u2) = m₂−4 =−f∗(um+4

2 ), for 1≤i≤

m−4 2 f

∗₍_u

2+i) = −(2i+

1) =−f∗(um+4 2 +i),f

∗₍_u

m+2

2 ) = −m+ 1 =−f

∗₍_v

1) and for 1≤i≤ n−₂1 f∗(v1+i) = m−1 +

2i = −f∗(vn+1

2 +i). Then f

∗₍_V₍_h_C

m, K1,ni))={±(m−1),±(m₂−4),±3,±5,±7, ...,±(m−

3),±(m+ 1),±(m+ 3),±(m+ 5), ...,±(m+n −2)}S

{2(m−1)}. Hence f is an edge pair sum labeling. The examples for the edge pair sum graph labeling of < C6, K1,3 >

and < C8, K1,3 > are shown in Figure 9. Case(iv). m is odd.

Subcase (a). m= 1,3(mod4).

For 1 ≤i≤ m−3

2 f(ei) =−2−i=−f(em+12 +i), f(e

m−1

2 ) = 1 =−f(em),f(e

m+1

(10)

t t

t

2

3

-1 -2

-3

1

5 7

-7

t t

t

t t _t

t

t t

7 9

-9 3

4

-2 -1

-4 -3

1 ₂

Figure 9: Edge pair sum labeling for the graph < C6, K1,3 >and < C8, K1,3 >

−f(e0₁) and for 1≤i≤ n−1 2 f(e

0

1+i) =m+2i=−f(e

0

n+1 2 +i

). The induced vertex labeling is

as follows: f∗(u1) = −2 =−f∗(v1), for 1≤i≤ m₂−5 f∗(u1+i) =−(5 + 2i) =−f∗(um+3 2 +i),

f∗(um−1

2 ) = −(

m−1

2 ) = −f

∗₍_u

m), f∗(um+1

2 ) = −1 = −f

∗₍_u

m+3

2 ) and for 1 ≤ i ≤

n−1 2

f∗(v1+i) = m+2i=−f∗(vn+1

2 +i). Thenf

∗₍_V₍_h_C

m, K1,ni))={±1,±2,±(m₂−1),±7,±9,±11, ...,±m, ±(m+ 2),±(m+ 4),±(m+ 6), ...,±(m+n−1)}.

Hence f is an edge pair sum labeling. Subcase (b). m= 0(mod3).

Define f(e1) = 2 = −f(em+3

2 ), f(e2) = −3 = f(e

0

1), for 1 ≤ i ≤ m−5

2 f(e3+i) = 3 +i = −f(em+5

2 +i), f(e

m+1

2 ) = −1 = −f(em) and for 1 ≤ i ≤

n−1 2 f(e

0

1+i) = m + 2i = −f(e0n+1

2 +i

). The induced vertex labeling is as follows: f∗(u1) = 6 = −f∗(um+5 2 ),

f∗(u2) = −1 = −f∗(u3), for 1 ≤ i ≤ m₂−7 f∗(u3+i) = −(7 + 2i) = −f∗(um+5 2 +i),

f∗(um+1 2 ) =

m−1

2 = −f

∗₍_u

m), f∗(um+3

2 ) = −3 =−f

∗₍_v

1) and for 1 ≤ i≤ n−₂1 f∗(v1+i) =

m+ 2i=−f∗(vn+1

2 +i). Thenf

∗₍_V₍_h_C

m, K1,ni))={±1,±3,±6,±(m₂−1),±9,±11,±13, ..., ±m,±(m + 2),±(m+ 4),±(m + 6), ...,±(m +n −1)}. Hence f is an edge pair sum labeling. The example for the edge pair sum graph labeling of < C9, K1,3 > is shown in

Figure 10.

Theorem 6. The graph hCm, K1,ni is an edge pair sum graph for m≥4 and n is even.

Proof. In [3] we have proved that Cm is and edge pair sum graph form ≥3. Letf be an

edge pair sum labeling of Cm.

Then f∗(V(Cm)) ={±K1,±K2, ...,±Kp

2} if p is even.

f∗(V(Cm)) ={±K1,±K2, ...,±Kp−1 2 }

S

{Kp

2} if p is odd.

Let the vertex and edge sets are as follows: V(hCm, K1,ni) = V(Cm)

S

{vi : 1 ≤ i ≤ n}

and E(hCm, K1,ni) =E(Cm)S{e

0

i : 1≤i≤n}

Define the edge labelingh :E(hCm, K1,ni)→ {±1,±2,±3, ...,±(q+n)}.

h(e) = f(e) if e∈E(Cm)

(11)

t t

t

t _t

t

1

2

-3 4

5 -1

-2

-4

-5

3

11

-11

Figure 10: Edge pair sum labeling for the graph < C9, K1,3 >

h(e0n

2+i) =−(q+ 2i) : 1≤i≤

n 2

The induced vertex labeling is as follows:

h∗(vi) =q+ 2i : 1≤i≤ n₂

h∗(vn

2+i) =−(q+ 2i) : 1≤i≤

n 2

Then h∗(V(hCm, K1,ni)) = {±K1,±K2, ...,±Kp

2} if pis even.

h∗(V(hCm, K1,ni)) ={±K1,±K2, ...,±Kp−1 2 }

S

{Kp

2} if p is odd.

Hence h is an edge pair sum labeling.

Corollary 7. The graph hCm∗K1,ni is an edge pair sum graph for m ≥4 and n is odd.

We use the previous edge labeling for this corollary. The example for the edge pair sum graph labeling of < C4∗K1,3 >is shown in Figure 11.

u u

u

u u

1

2 -1

-2

3

7 _-7

Figure 11: Edge pair sum labeling for the graph < C4∗K1,3 >

References

[1] J.A.Gallian, A dynamic survey of graph labeling, Electronic J.Combin.,(2014).

[2] F.Harary, Graph Theory, Addison Wesley, Massachusetts, 1972.

[3] P. Jeyanthi,T.Saratha Devi, Edge pair sum labeling, Journal of Scientific Research,5

(12)

[4] P. Jeyanthi,T.Saratha Devi, On edge pair sum labeling of graphs, International Jour-nal of Mathematics Trends and Technology,7, (2), (2014), 106 - 113.

[5] P. Jeyanthi,T.Saratha Devi, Edge pair sum labeling of spider graph, Journal of Algo-rithms and Computation, 45 (1), (2014), 25 - 34.

[6] P. Jeyanthi,T.Saratha Devi,Gee-Choon Lau, Edge pair sum labeling of W T(n : k) Tree, Global Journal of Pure and Applied Mathematics,11, (3), (2015), 1523 - 1539.

[7] P. Jeyanthi,T.Saratha Devi, Gee-Choon Lau, Some results of edge pair sum labeling,

Electronic Notes in Discrete Mathematics,48 (2015), 169 - 173.

[8] P. Jeyanthi,T.Saratha Devi, Some edge pair sum graphs, Journal of Discrete Mathe-matical Science and Cryptography, (48),(2015), 169-173.

[9] P. Jeyanthi,T.Saratha Devi, New results on edge pair sum graphs,International Jour-nal of Mathematics And its Applications, in press.

[10] P. Jeyanthi,T.Saratha Devi, Edge pair sum labeling of some cartesian product graphs,

Discrete Mathematics Algorithms and Applications, in press.

[11] A.Nagarajan, F.Vasuki and S.Arockiaraj, Super Mean Number of a Graph, Kragu-jevac Journal of Mathematics,36 (1), (2012), 93-107.