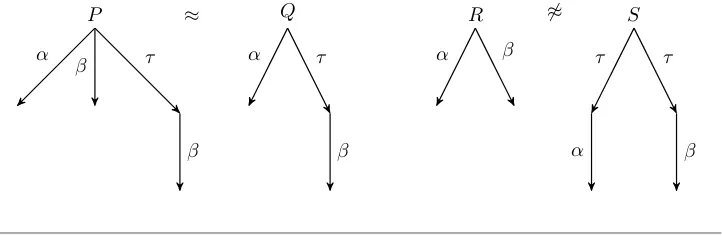
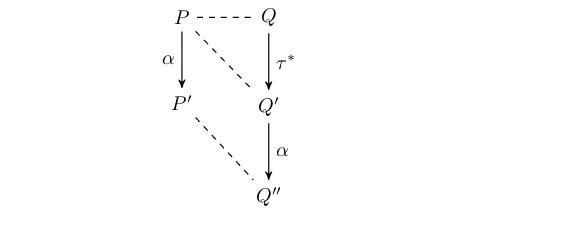
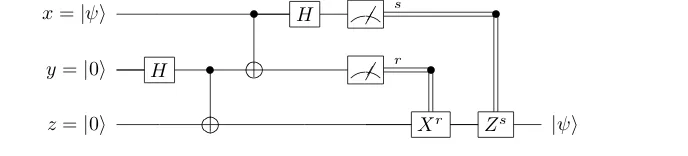
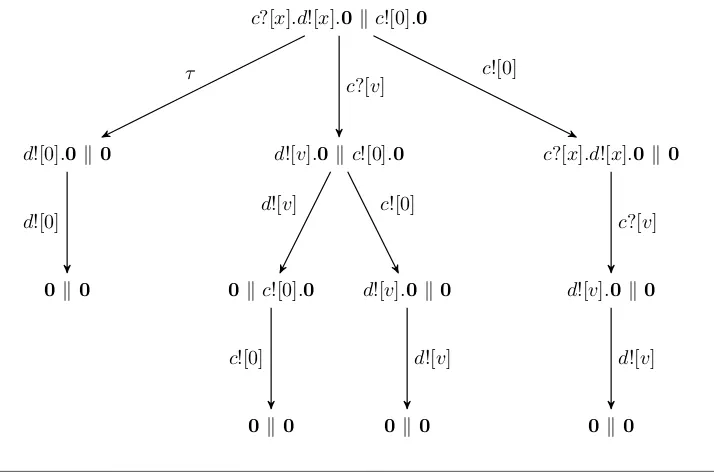
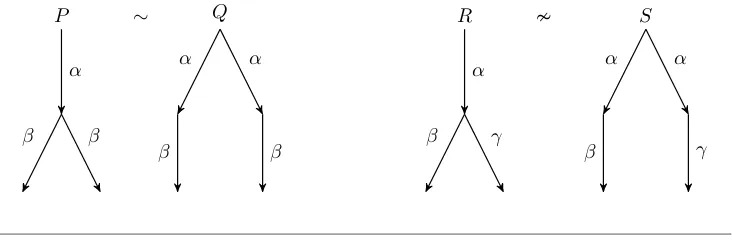
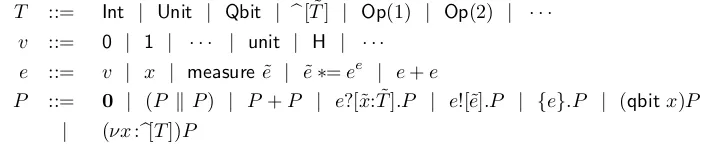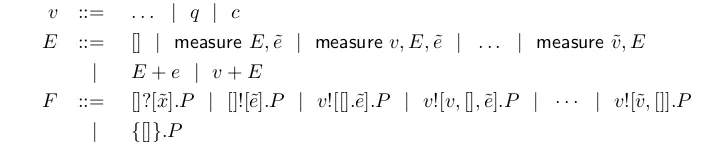Formal verification techniques using quantum process calculus
Full text
Figure
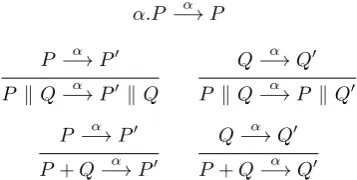
Related documents
A STUDYON IMPACT OF PROMOTIONAL STRATEGIES ON CONSUMER BUYING BEHAVIOR TO SHOPPING
You can access Academic and Personal Support on the ‘Support’ tab in MyBeckett, which may direct you to support services such as Student Experience Team, Wellbeing and the
A series of univariate and multivar- iate linear regression models were used to determine the vari- ables associated with the frequency of CD27 ⫺ and CD28 ⫺ cells within the pool
The resulting eigen value problem is solved using Regular perturbation technique with wave number a as perturbation parameter and the expression for the Thermal Marangoni Number
For example, advances that reduce emissions from electricity production, such as the development of affordable technologies for reducing emissions from coal production or
Sequences under this name are deposited in GenBank and Jaklitsch & oglmayr (2014) have commented on its phylogenetic position in their list of Trichoderma/.. Hypocrea