String theory clues for the low–ℓ CMB ?
Full text
Figure
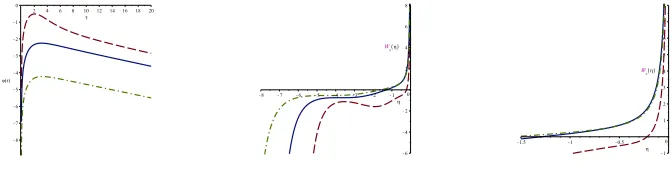

![Figure 6. WMAP9 determination [21] of the CMB angular power spectrum (left), the raw data for its low–ℓportion (center) and the corresponding PLANCK determination [20] (right)](https://thumb-us.123doks.com/thumbv2/123dok_us/8173633.1364952/9.482.72.411.130.222/figure-determination-angular-spectrum-portion-corresponding-planck-determination.webp)
Related documents
The optimized MWPA was concentrated and extracted using ethyl acetate and was further determined for its antimicrobial properties against Gram positive and Gram negative bacterial
Variations in the concentration of elements in plant samples of the tunnel #504 on the sampling profi le Analysis of the results suggests that the point with the highest
Pertaining to the secondary hypothesis, part 1, whether citalopram administration could raise ACTH levels in both alcohol-dependent patients and controls, no significant
Thus, this study is designed to highlight the status of uncontrolled hypertension in patients with type 2 diabetes and determine the associated factors, which may affect the
As a service provider of credit grantors and larger market participant collection agencies, we know the following compliance requirements have been required of agencies and debt
ally illustrate how VLANs restrict forwarding to use safe paths in a transitional network, we first consider a straightforward, yet impractical scheme: For every pair of SDN
The gratings are introduced to make the antenna to perform better radiation characteristics of a comparatively stable, symmetrical pattern and low side lobes over the operating band

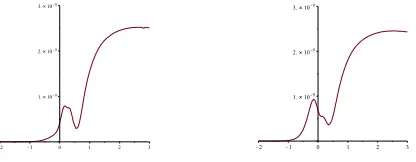
![Figure 10. The best choice that we could find for a power spectrum resulting from a two–exponential system withandPLANCK data [22] (right) gaveγ = 0.08 (left) and a small gaussian bump, as in eq](https://thumb-us.123doks.com/thumbv2/123dok_us/8173633.1364952/12.482.87.398.68.152/figure-choice-spectrum-resulting-exponential-withandplanck-gaveg-gaussian.webp)