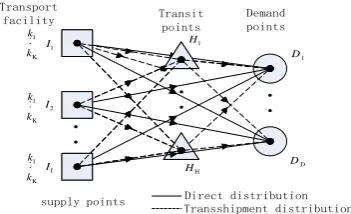
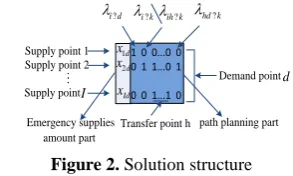
A Modified Discreet Particle Swarm Optimization for a Multi-level Emergency Supplies Distribution Network
Full text
Figure


Related documents
Results: In order to characterize the role of the ependymal barrier in the immunopathogenesis of NCC, we isolated ependymal cells using laser capture microdissection from mice
Cu(II), Zn(II) exhibit tetragonal structure were as Mo(II) and Fe(II) complexes exhibit octahedral structure.. The proposed structure of Cu (II), Zn (II), Mo (II) and Fe (II)
The segment results benefited from capitalizing direct project related costs since the LNG project agreement with the government of Papua New Guinea was signed
Methods: This prospective case–control study in the medical–surgical intensive care unit of a university hospital included consecutive adults patients with septic shock and
Considering the surfeit of pitfalls associated with the lack of transparency in nonprofit organizations, and the apparent number of boards of national
Based on their review of the literature, one can conclude that university students are not fully aware of forms of plagiarism as cheating, stealing and dishonest acts;
Based on previous reports of acute psychosis [6,7], surveys of enzyme activity in psychiatric samples [5,14], genetic linkage/association studies [4,15–17,33], and on the series
The purpose of this study was to examine the experiences of secondary teachers who participated in school-based mentoring programs and their perspectives on the impact this