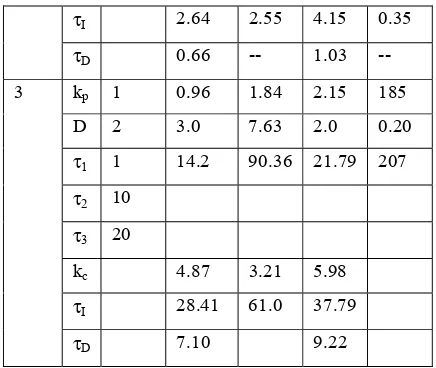
An Improved Relay Auto Tuning of PID Controllers for SOPTD Systems

The paper presents design of biodegradable resonator working at ISM band frequency.. The paper is utilized as substrate and think copper sheets are utilized as resonator which

It included four parts, the first part includes questions related to pharmacy students’ perceptions and knowledge about antimicrobial stewardship, second part

VINCI’s 2014 half-year financial statements show slight growth in revenue on a comparable structure basis, stable cash flow from operations before tax and

Fechler, N.; Fellinger, T.-P.; Antonietti, M., Template-Free One-Pot Synthesis of Porous Binary and Ternary Metal Nitride@N-Doped Carbon Composites from Ionic Liquids, Chemistry

Purification of plant viruses were largely done in late nineties, there are previously described purification protocols for bymoviruses, such as Barley Yellow Mosaic

Mapping metabolic changes associated with early Radiation Induced Lung Injury post conformal radiotherapy using hyperpolarized (13)C-pyruvate Magnetic Resonance

Substantial antifungal activity shown by methanolic extract in which zone of inhibition ranged from 22mm to 32mm while other fractions also shown activity such as

Expression o f transform ing growth factor beta receptors in normal human colon and sporadic adenocarcinom as.. Elevated serum in su lin -lik e growth factor (IGF)-II and