Asymmetric bounded neural control for an uncertain robot by state feedback and output feedback

(1)

Asymmetric Bounded Neural Control for an

Uncertain Robot by State Feedback and Output

Feedback

Linghuan Kong, Wei He,

Senior Member, IEEE,

Yiting Dong,

Student Member, IEEE,

Long Cheng,

Senior

Member, IEEE,

Chenguang Yang,

Senior Member, IEEE,

Zhijun Li,

Senior Member, IEEE

Abstract

—In this paper, an adaptive neural bounded control

scheme is proposed for an

n-link rigid robotic manipulator with

unknown dynamics. With combination of neural approximation

and backstepping technique, an adaptive neural network control

policy is developed to guarantee the tracking performance of

the robot. Different from the existing results, the bounds of the

designed controller are known

a priori

, and they are determined

by controller gains,

making them applicable within actuator

limitations

. Furthermore, the designed controller is also able

to compensate the effect of unknown robotic dynamics. Via

Lyapunov stability theory, it can be proved that all the signals

are uniformly ultimately bounded (UUB). Simulations are carried

out to verify the effectiveness of the proposed scheme.

Index Terms

—Neural networks, Asymmetrically bounded

in-puts, A robotic manipulator, Adaptive control

I. I

NTRODUCTION

Robots have a wide range of applications in various fields

such as prospecting, navigation, aviation and so on [1]–[8].

Control design and stability analysis for a robot are

increas-ingly important and have received considerable attention [9],

[10]. A significant topic in the robot field is trajectory tracking

[11]. Thus, many research results have been obtained in the

past decades [12]–[14]. However, an avoidable challenge for

controller design is that there exists model uncertainty due to

the fact that robots are highly nonlinear and strongly coupled

[15]–[18].

Model-based control has been proved to be effective in

practical applications. An inevitable shortcoming for

model-This work was supported in part by the National Natural Science Foundation of China under Grant 61873298, Grant 61873268, Grant 61633016, Grant 61751310 and Grant 61573147, in part by the Anhui Science and Technology Major Program under Grant 17030901029, in part by the Beijing Science and Technology Project (Grant No. Z181100003118006), in part by the Beijing Municipal Natural Science Foundation (Grant No. L182060), and in part by the Engineering and Physical Sciences Research Council (EPSRC) under Grant EP/S001913.

L. Kong and W. He are with School of Automation and Electrical Engineer-ing, University of Science and Technology BeijEngineer-ing, Beijing 100083, China, and also with the Institute of Artificial Intelligence, University of Science and Technology Beijing, Beijing 100083, China. (Email: weihe@ieee.org)

Y. Dong is with the Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA.

L. Cheng is with the State Key Laboratory of Management and Control for Complex Systems, Institute of Automation, Chinese Academy of Sciences, Beijing 100190, China, and also with the University of the Chinese Academy of Sciences, Beijing 100049, China.

C. Yang is with Bristol Robotics Laboratory, University of the West of England, Bristol, BS16 1QY, UK.

Z. Li is with Department of Automation, University of Science and Technology of China, Hefei, China.

(2)

nonstrict-feedback systems with input saturation. In [70], a novel

adap-tive sliding mode controller is designed for Takagi-Sugeno

fuzzy systems with actuator saturation and system uncertainty.

An asymmetric saturation situation may be encountered if

the actuators partially loss their effectiveness for an uncertain

robot, due to motor fault, change of mechanical structure, etc,

which drives us to solve the asymmetric saturation constraint

problems for an uncertain robot. In [66]–[70], the bounds of

the designed controller are considered to be unknown for the

controller design, which motivates us to further investigate the

adaptive neural network control with asymmetric and known

bounds for an

n

-link rigid robotic manipulator with uncertain

dynamics, making the designed controller applicable within

actuator limitations.

Motivated by above observations, this paper focuses on

the adaptive bounded control for an

n

-link rigid robotic

manipulator with unknown dynamics, where the bounds of

the designed controller are asymmetric and known

a prior

and

furthermore can be predetermined by changing control gains,

making the designed controller applicable within actuator

limitations

. Neural networks are employed to approximate

unknown robotic dynamics. A high-gain observer is introduced

to estimate the immeasurable states.

Compared with the previous works, the main contributions

are summarized as follows:

1) Compared with [66]–[70], a main feature in this paper is

that the bounds of the designed controller are asymmetric

and known

a priori

, and furthermore they are

predeter-mined by changing control gains.

2) In [66], an additional auxiliary variable is designed to

eliminate the effect of input saturation. Compared with

[66], we directly adopt hyperbolic tangent function

tan-h

(

·

)

to obtain the bounded control. Thus, the structure

of the designed controller in this paper may be more

simpler to some extent, which is beneficial to controller

implementation and real-time control.

The structure of the paper is presented. Section II shows

preliminaries and problem formulation. The main results are

given in Section III. In Section IV, some simulation examples

are provided to demonstrate the effectiveness of the proposed

method. Finally, Section V concludes this paper.

Notations 1:

Let

∥ • ∥

be the Euclidean norm of a vector

or a matrix. Let

A

i

(

i

= 1

, . . . , n

)

denote the

i

th row and the

i

th diag element

A

ii

of the vector

A ∈

R

n

and the matrix

A ∈

R

n_×n

, respectively. The symbol “

I

” is used to denote an

identity matrix with appropriate dimensions.

II. P

RELIMINARIES AND

P

ROBLEM

F

ORMULATION

A. Problem Formulation

Consider an

n

-link rigid robotic manipulator model [71] in

joint space as

M

(

q

)¨

q

+

C

(

q,

q

˙

) ˙

q

+

G

(

q

) =

µ

(1)

where

q

∈

R

n

,

q

˙

∈

R

n

,

q

¨

∈

R

n

denote the vector of joint

position, velocity and acceleration,

M

(

q

)

∈

R

n×n

denotes

the positive definite quality inertia matrix,

C

(

q,

q

˙

)

∈

R

n_×n

denotes the coriolis and centrifugal matrix,

G

(

q

)

∈

R

n

denotes

the gravitational forces,

µ

∈

R

n

denotes the control torque

vector and satisfies

µ

−_ci

≤

µ

i

≤

µ

+ci

(2)

where

µ

+_ci

∈

R

+

,

µ

−_ci

∈

R

−

,

i

= 1

, . . . , n

, denote the upper

and lower bound of

µ

i

, respectively.

The control objective in this paper is to design an

asymmet-rically bounded control scheme ensuring: 1) the robot given

in (1) can track the reference trajectory

x

d

with an acceptable

accuracy; 2) tracking errors are uniformly ultimately bounded

(UUB).

Assumption 1:

[72] System matrixes

M

(

q

)

,

C

(

q,

q

˙

)

and

G

(

q

)

are unknown, and furthermore

M

−1

(

q

)

exists.

Property 1:

[72]

M

˙

(

q

)

−

2

C

(

q,

q

˙

)

is a skew symmetric

matrix.

∀

x

∈

R

n

,

x

T

( ˙

M

(

q

)

−

2

C

(

q,

q

˙

))

x

= 0

.

B. Radial Basis Function Neural Networks (RBFNNs)

In the consequent design, unknown nonlinear functions

would be approximated by RBFNNs in the following form.

h

n

(

Z

) = ˆ

θ

T

φ

(

Z

)

(3)

where

h

n

(

Z

)

is any nonlinear function,

Z

∈

Ω

Z

⊂

R

q

is the input vector,

θ

ˆ

= [ˆ

θ

1

, . . . ,

θ

ˆ

l

]

T

∈

R

l

is the weight

vector,

l >

1

is the neural network node number, and

φ

(

Z

) = [

φ

1

(

Z

)

, . . . , φ

l

(

Z

)]

T

with

φ

i

(

Z

)

chosen as the

Gaussian radial basis function.

φ

i

(

Z

)

is given by

φ

i

(

Z

) = exp[

−

(

Z

−

ϱ

i

)

T

(

Z

−

ϱ

i

)

η

2

i

]

(4)

where

ϱ

i

= [

ϱ

i1

, . . . , ϱ

iq

]

T

is the center of the receptive field

and

η

i

is the width of the Gaussian radial basis function,

i

=

1

, . . . , n

.

Lemma 1:

[73] For given accuracy

ϵ >

0

with sufficiently

large node number

l

, neural networks (3) can approximate any

continuous nonlinear function

h

(

Z

)

defined in the compact set

Ω

⊂

R

q

such that

h

(

Z

) =

θ

T

φ

(

Z

) +

ϵ

(

Z

)

,

∀

Z

∈

Ω

⊂

R

q

(5)

where

θ

is the optimal weight defined as

θ

:= arg min

ˆ

θ_⊂_Rl

{

sup

Z_∈Ω

|

h

(

Z

)

−

θ

ˆ

T

φ

(

Z

)

|

}

,

(6)

and

ϵ

(

Z

)

is the approximation error satisfying

∥

ϵ

(

Z

)

∥ ≤

ϵ

¯

with

¯

ϵ

being positive constants.

Lemma 2:

[73] Given that the Gaussian radial basis

func-tion with

Z

ˆ

=

Z

−

γν

¯

being the input vector, where

ν

is a

bounded vector and

¯

γ

is a positive constant, then we have

φ

i

( ˆ

Z

) = exp[

−

( ˆ

Z

−

ϱ

i

)

T

( ˆ

Z

−

ϱ

i

)

η

2

i

]

, i

= 1

, . . . , l

(7)

φ

( ˆ

Z

) =

φ

(

Z

) + ¯

γφ

(8)

∥

φ

(

Z

)

∥

2

≤

l

(9)

where

φ

is a bounded function vector.

C. Useful Properties, Definitions and Lemmas

(3)

and maximum eigenvalues of

A

. For

∀

x

∈

R

n

, there is

λ

min

(

A

)

||

x

||

2

≤

x

T

A

x

≤

λ

max

(

A

)

||

x

||

2

.

η

i

,

i

= 1

, . . . , n

,

Definition 1:

Define the diagonal matrix

Tanh

2

(

.

)

∈

R

n×n

as follows:

Tanh

2

(

η

) = diag[tanh

2

(

η

1

)

, . . . ,

tanh

2

(

η

n

)]

(10)

where

η

= [

η

1

, . . . , η

n

]

T

∈

R

n

.

Lemma 3:

Assume that

f

(

µ

)

is an asymmetric saturation

function represented as

f

(

µ

) =











µ

+

c

if

µ

+c

< µ

µ

if

µ

−_c

≤

µ

≤

µ

+_c

µ

−_c

Otherwise

(11)

where

µ

+c

and

µ

−c

are the upper and lower bound of

µ

,

respectively. When

µ

=

µ

+c

or

µ

=

µ

−c

, there is a sharp corner.

Then a novel smooth function is introduced to approximate

this saturation function in the following form.

f

(

µ

) =

δµ

+_c

tanh(

µ

+c

) + (1

−

δ

)

µ

−_c

tanh(

µ

−c

) +

p

(

µ

)

(12)

where

δ

denotes a switching function defined as [74]

δ

=

{

1

if

µ

≥

0

Otherwise

(13)

and

p

(

µ

)

denotes a bounded function. Then we present a proof

showing that

p

(

µ

)

is bounded.

Proof:

Two cases are considered as follows:

•

Case one:

µ > µ

+

c

. (12) is rewritten as

f

(

µ

) =

µ

+

c

tanh(

µ µ+c

)+

p

(

µ

)

. With combination of (11), it follows

that

|

p

(

µ

)

|

=

|

µ

+

c

(1

−

tanh(

µ µ+c

))

| ≤ |

µ

+

c

|

, which

illustrates that

p

(

µ

)

is bounded for the case

µ > µ

+

c

.

Similar proof can also be presented for the case

µ

−_c

> µ

.

•

Case two:

0

≤

µ

≤

µ

+

c

. (12) is rewritten as

f

(

µ

) =

µ

+_c

tanh(

µ

µ+c

)+

p

(

µ

)

. With combination of (11), it follows

that

p

(

µ

) =

µ

−

µ

+c

tanh(

µ µ+c

)

≤

µ

+c

(1

−

tanh(

µ µ+c

))

,

similarly, implying that

p

(

µ

)

is bounded when

0

≤

µ

≤

µ

+

c

. Similar proof can also be presented for the case

µ

−c

≤

µ <

0

.

III. C

ONTROL

D

ESIGN

For the convenience of controller design, before controller

design, we define

x

1

=

q

and

x

2

= ˙

q

, and then (1) can be

rewritten as

˙

x

1

=

x

2

(14)

˙

x

2

=

M

−1

(

µ

−

G

−

Cx

2

)

(15)

where

x

1

= [

x

11

, . . . , x

1n

]

T

,

x

2

= [

x

21

, . . . , x

2n

]

T

. In the

subsequent design,

M

,

C

and

G

denote

M

(

x

1

)

,

C

(

x

1

, x

2

)

and

G

(

x

1

)

, respectively.

A. Model-based Control Design

Tracking errors are defined as

z

1

=

x

1

−

x

d

(16)

z

2

=

x

2

−

α

(17)

where

α

is defined as

α

=

−

A

+ ˙

x

d

(18)

where

A

= [

k1ln cosh(z11)

tanh(z11

, . . . ,

knln cosh(z1n)

tanh(z1n)

]

T

∈

R

n

, and

K

= diag[

k

1

, . . . , k

n

]

∈

R

n×n

is a positive definite matrix.

Then error dynamics is calculated as

˙

z

1

=

z

2

−

A

(19)

˙

z

2

=

M

−1

(

µ

−

G

−

Cx

2

)

−

α

˙

(20)

Choose a positive Lyapunov function candidate as

V

1

=

n

∑

i=1

ln(cosh(

z

1i

)) +

1

2

z

T

2

M z

2

(21)

Substituting (19) and (20) into the time derivative of (21), we

get

˙

V

1

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

)) +

n

∑

i=1

z

2i

tanh(

z

1i

)

+

z

₂T

(

µ

−

G

−

Cα

−

M

α

˙

)

(22)

Then, model-based control

µ

is designed as

µ

=

−

tanh(

z

1

)

−

K

1

tanh(

z

2

) +

B

tanh(

B

−1

ψ

)

(23)

where

µ

= [

µ

1

, . . . , µ

n

]

T

∈

R

n

,

K

1

= diag[

k

11

, . . . , k

1n

]

∈

R

n×n

is a positive definite matrix, and

B

= diag[

δ

i

µ

+i

+ (1

−

δ

i

)

µ

−i

]

∈

R

n×n

with

µ

−i

being negative constants and

µ

+

i

being positive constants. It should be emphasized that

µ

−_i

and

µ

+_i

are also considered as adjustable control gains. Auxiliary

variable

ψ

is defined as

ψ

i

=

δ

i

µ

+i

arctanh

(

G

+

Cα

+

M

α

˙

)

i

µ

+_i

)

+ (1

−

δ

i

)

µ

−i

arctanh

(

G

+

Cα

+

M

α

˙

)

i

µ

−_i

)

(24)

where

arctanh(

·

)

denotes the inverse function of

tanh(

·

)

, and

ψ

= [

ψ

1

, . . . , ψ

n

]

T

∈

R

n

. We assume that initial values satisfy

µ

−_i

<

(

G

+

Cα

+

M

α

˙

)

i

(0)

< µ

+i

.

δ

i

is a switching function

defined as

δ

i

=

{

1

if (

G

+

Cα

+

M

α

˙

)

i

>

0

Otherwise

(25)

Substituting (23) into (22), we get

˙

V

1

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

z

T2

K

1

tanh(

z

2

)

+

z

2T

(

B

tanh(

B

−1

ψ

)

−

G

−

Cα

−

M

α

˙

)

(26)

Define

f

(

µ

) =

G

+

Cα

+

M

α

˙

, and by ultilizing Lemma 3, we

have

f

(

µ

) =

B

tanh(

B

−1

ψ

) +

p

(

µ

)

, where

p

(

µ

)

denotes the

approximation error, and furthermore it is assumed that

p

(

µ

)

(4)

positive constants. Thus we have

z

T

2

(

B

tanh(

B

−1

ψ

)

−

G

−

Cα

−

M

α

˙

) =

−

z

T

2

p

(

µ

)

≤

1 2

z

T

2

z

2

+

12

p

¯

2

. According to Taylor

expansion, we know

tanh(

z

2

) =

z

2

+

o

(

z

2

)

,

∥

z

2

∥

<

π

2

(27)

where

o

(

z

2

) =

−

1₃

z

32

+

2 15

z

5 2

−

17 315

z

7

2

+

· · ·

, and in the interval

∥

z

2

∥

<

π₂

,

o

(

z

2

)

is bounded, i.e.,

∥

o

(

z

2

)

∥ ≤

o

¯

with

¯

o

being

a positive constant. With aid of Young’s inequality, thus (26)

becomes

˙

V

1

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

z

T2

K

1

z

2

−

z

2T

K

1

o

(

z

2

)

+

1

2

z

T

2

z

2

+

1

2

p

¯

2

≤ −

κ

1

V

1

+

C

1

(28)

where

κ

1

=

min

{

min

i=1,...,n

k

i

,

λmin(K1−I)

λmax(M)

}

,

C

1

=

1

2

λ

max

(

K

T

1

K

1

)¯

o

2

+

1₂

p

¯

2

. To ensure

κ

1

>

0

, controller

param-eters should satisfy

min

i=1,...,n

k

i

>

0

and

λ

min

(

K

1

−

I

)

>

0

.

Then the following theorem is obtained.

Theorem 1:

For robotic system (1), by designing

model-based control input (23), the controller can ensure that

all the error signals are UUB. Furthermore,

z

1

eventu-ally converges to the compact set defined as

Ω

z1

:=

{

z

1

∈

R

n

||

z

1i

| ≤

√

2

e

H1

, i

= 1

, . . . , n

}

, and

z

2

eventual-ly converges to the compact set defined as

Ω

z2

:=

{

z

2

∈

R

n

|||

z

2

|| ≤

√

2H1

λmin(M)

}

, where

H

1

=

V

1

(0) +

C_κ₁1

.

Proof

: See Appendix

Remark 1:

If

δ

i

= 1

, (23) can be rewritten as

µ

i

=

−

tanh(

z

1i

)

−

k

1i

tanh(

z

2i

) +

µ

+i

tanh(

ψi

µ+

i

)

,

i

= 1

, . . . , n

,

and by the utilization of the property of the continuous

function

tanh(

·

)

, we know that

µ

i

is upper bounded, i.e.,

µ

i

≤

1 +

k

1i

+

µ

+i

. If

δ

i

= 0

, (23) can reduce to

µ

i

=

−

tanh(

z

1i

)

−

k

1i

tanh(

z

2i

) +

µ

−i

tanh(

ψi

µ−_i

)

,

i

= 1

, . . . , n

,

and we further know that

µ

i

is also lower bounded, i.e.,

µ

i

≥ −

(1 +

k

1i

+

µ

−i

)

. Then, defining

µ

+

ci

= 1 +

k

1i

+

µ

+i

and

µ

−_ci

=

−

(1 +

k

1i

+

µ

−i

)

implies

µ

−ci

≤

µ

i

≤

µ

+ci

, i

= 1

, . . . , n

.

It should be noted that

k

1i

,

µ

+i

and

µ

−i

,

i

= 1

, . . . , n

can also

be considered as controller gains, which, if necessary, may

also change for both satisfactory tracking performances and

suitable bounds of controllers, making the controller applicable

within actuator limitations.

B. State-Feedback-Based Adaptive Neural Control Design

Assume that

M

,

C

and

G

are unknown such that

model-based control (23) is unavailable in practice. Furthermore,

auxiliary variable

ψ

given in (24) is also unknown. Then neural

networks are employed to approximate

ψ

in the following

form.

θ

T

φ

(

Z

) =

ψ

+

ϵ

(

Z

)

(29)

where

θ

is the desired weight vector,

Z

= [

x

T1

, x

2T

, z

T1

, z

2T

]

T

∈

R

4n

is the input of RBFNNs, and

ϵ

(

Z

)

is the approximation

error satisfying

∥

ϵ

(

Z

)

∥ ≤

¯

ϵ

with

¯

ϵ

being a positive constant.

Then an adaptive neural network controller is designed as

µ

=

−

tanh(

z

1

)

−

K

1

tanh(

z

2

) +

B

tanh(

B

−1

ψ

ˆ

)

(30)

ˆ

ψ

= ˆ

θ

T

φ

(

Z

)

(31)

˙ˆ

θ

i

=

−

Γ

i

(

φ

(

Z

)

z

2i

+

ς

θ

ˆ

i

)

, i

= 1

, . . . , n

(32)

where

K

1

= diag[

k

11

, . . . , k

1n

]

∈

R

n×n

is a positive definite

matrix,

B

= diag[

δ

i

µ

+i

+ (1

−

δ

i

)

µ

−i

]

∈

R

n×n

with

δ

i

defined

as

δ

i

=

{

1

if ˆ

θ

T

i

φ

(

Z

)

≥

ℓ

i

0

Otherwise

,

(33)

ℓ

i

,

θ

˜

Ti

φ

(

Z

) +

ϵ

i

(

Z

)

,

(ˆ

•

)

denotes the estimation of

(

•

)

satisfying

(˜

•

) = (ˆ

•

)

−

(

•

)

,

Γ

i

is a symmetric positive

definite matrix, and

ς

is a small constant which improves the

robustness.

Remark 2:

Note that switching function

δ

i

given in (25) is

based on an assumption that

M

,

C

and

G

are all known.

However, in this section

M

,

C

and

G

are assumed to be

unknown, which causes switching function

δ

i

given in (25) to

be ineffective. Therefore switching function

δ

i

need redesigned

again. Due to the fact that

θ

T

φ

(

Z

) = ˆ

θ

T

φ

(

Z

)

−

θ

˜

T

φ

(

Z

)

,

(29) is rewritten as

ψ

= ˆ

θ

T

φ

(

Z

)

−

θ

˜

T

φ

(

Z

)

−

ϵ

(

Z

)

. Let us

recall switching function

δ

i

given in (25) and consider the

fact that

arctanh(

.

)

is an odd function, and we know: 1)

when

(

G

+

Cα

+

M

α

˙

)

i

≥

0

, it follows that

ψ

i

≥

0

and

ˆ

θ

T

i

φ

(

Z

)

≥

θ

˜

iT

φ

(

Z

) +

ϵ

i

(

Z

)

; 2) when

(

G

+

Cα

+

M

α

˙

)

i

<

0

,

it follows that

ψ

i

<

0

and

θ

ˆ

iT

φ

(

Z

)

<

θ

˜

T

i

φ

(

Z

) +

ϵ

i

(

Z

)

. By

defining

ℓ

i

= ˜

θ

Ti

φ

(

Z

) +

ϵ

i

(

Z

)

, one can obtain the switch

function

δ

i

given in (33),

i

= 1

, . . . , n

.

Similar to analysis in Remark 1, we can conclude that

µ

i

, i

=

1

, . . . , n

given in (30) are bounded, i.e.,

µ

−_ci

≤

µ

i

≤

µ

+ci

, i

=

1

, . . . , n

, are guaranteed. A Lyapunov function candidate is

chosen as

V

2

=

n

∑

i=1

ln(cosh(

z

1i

)) +

1

2

z

T

2

M z

2

+

1

2

n

∑

i=1

˜

θ

T_i

Γ

−_i1

θ

˜

i

(34)

Substituting (19) and (20) into the time derivative of (34), we

get

˙

V

2

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

)) +

n

∑

i=1

z

2i

tanh(

z

1i

)

+

z

T₂

(

µ

−

G

−

Cα

−

M

α

˙

) +

n

∑

i=1

˜

θ

_iT

Γ

−_i 1

θ

˙ˆ

i

(35)

Substituting (30) and (32) into (35), we further get

˙

V

2

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

n

∑

i=1

˜

θ

T_i

(

φ

(

Z

)

z

2i

+

ς

θ

ˆ

i

)

−

z

₂T

K

1

tanh(

z

2

) +

z

T2

(

B

tanh(

B

−

1

ψ

ˆ

)

−

G

−

Cα

−

M

α

˙

)

(36)

Define

f

(

µ

) =

G

+

Cα

+

M

α

˙

, and by utilizing Lemma 3, we

have

f

(

µ

) =

B

tanh(

B

−1

ψ

) +

p

(

µ

)

, where

p

(

µ

)

denotes the

approximation error, and furthermore it is assumed that

p

(

µ

)

is upper bounded, i.e.,

∥

p

(

µ

)

∥ ≤

p

¯

with

p

¯

being unknown

positive constants. Then we know that

z

T

(5)

G

−

Cα

−

M

α

˙

)

becomes

z

T

2

B

(tanh(

B

−1

ψ

ˆ

)

−

tanh(

B

−1

ψ

))

−

z

T

2

p

(

µ

)

. According to mean value theorem, we have

tanh(

B

−_i 1

ψ

ˆ

i

)

−

tanh(

B

i−1

ψ

i

)

= (1

−

tanh

2

(

η

i

))(

B

i−1

( ˆ

ψ

i

−

ψ

i

))

(37)

where

η

i

∈

(

B

i−1

ψ

ˆ

i

, B

i−1

ψ

i

)

or

η

i

∈

(

B

i−1

ψ

i

, B

−i 1

ψ

ˆ

i

)

and

B

−1

= diag[

B

−1

1

, . . . , B

n−1

]

,

i

= 1

, . . . , n

. Using (29)

and (31), we have

tanh(

B

_i−1

ψ

ˆ

i

)

−

tanh(

B

i−1

ψ

i

) = (1

−

tanh

2

(

η

i

))

B

i−1

(˜

θ

T

i

φ

(

Z

) +

ϵ

i

(

Z

))

,

i

= 1

, . . . , n

. Therefore,

(36) becomes

˙

V

2

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

n

∑

i=1

˜

θ

_iT

(

φ

(

Z

)

z

2i

+

ς

θ

ˆ

i

)

−

z

T₂

K

1

tanh(

z

2

) +

z

2T

(

I

−

Tanh

2

(

η

))

×

(˜

θ

T

φ

(

Z

) +

ϵ

(

Z

))

−

z

₂T

p

(

µ

)

(38)

Note that

∑

n_i₌₁

θ

˜

T

i

φ

(

Z

)

z

2i

=

z

2T

θ

˜

T

φ

(

Z

)

and consider (27),

we further have

˙

V

2

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

n

∑

i=1

˜

θ

T_i

ς

θ

ˆ

i

−

z

2T

K

1

z

2

−

z

2T

K

1

o

(

z

2

)

−

z

2T

Tanh

2

(

η

)(˜

θ

T

φ

(

Z

) +

ϵ

(

Z

))

+

z

₂T

ϵ

(

Z

)

−

z

₂T

p

(

µ

)

(39)

In

terms

of

Young’s

inequality,

we

obtain

z

₂T

K

1

o

(

z

2

)

≤

1₂

z

2T

z

2

+

1₂

λ

max

(

K

1T

K

1

)¯

o

2

,

−

∑

n

i=1

θ

˜

T

i

ς

θ

ˆ

i

≤

−

₂ς

∑

n i=1

θ

˜

T

i

θ

˜

i

+

ς₂

∑

n

i=1

θ

T i

θ

i

,

−

z

T

2

Tanh

2

(

η

)˜

θ

T

φ

(

Z

)

≤

ϱ2₁

2

z

T

2

z

2

+

l

2

2ϱ2 1

∑

n i=1

θ

˜

T i

θ

˜

i

,

−

z

2T

Tanh

2

(

η

)

ϵ

(

Z

)

≤

1₂

z

2T

z

2

+

1₂

ϵ

¯

2

,

z

2T

ϵ

(

Z

)

≤

12

z

T

2

z

2

+

1₂

¯

ϵ

2

,

and

−

z

2T

p

(

µ

)

≤

12

z

T

2

z

2

+

1₂

p

¯

2

, where

ϱ

1

is an adjustable

parameter. Thus, we have

˙

V

2

≤ −

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

z

2T

(

K

1

−

(

4 +

ϱ

2

1

2

)

I

)

z

2

−

1

2

(

ς

−

l

2

ϱ

2 1

)

∑

n

i=1

˜

θ

_iT

θ

˜

i

+

1

2

λ

max

(

K

T

1

K

1

)¯

o

2

+

ς

2

n

∑

i=1

θ

T_i

θ

i

+ ¯

ϵ

2

+

1

2

p

¯

2

≤ −

κ

2

V

2

+

C

2

(40)

where

κ

2

= min

{

min

i=1,...,n

k

i

,

i=1

min

,...,n

(

ς

−

l

2

ϱ

2 1

)

1

λ

max

(Γ

−i 1

)

,

λ

min

(

2

K

1

−

(4 +

ϱ

21

)

I

)

1

λ

max

(

M

)

}

C

2

=

1

2

λ

max

(

K

T

1

K

1

)¯

o

2

+

ς

2

n

∑

i=1

θ

_iT

θ

i

+ ¯

ϵ

2

+

1

2

p

¯

2

To guarantee

κ

2

>

0

, controller parameters should be chosen

to satisfy:

min

i=1,...,n

k

i

>

0

,

min

i=1,...,n

(

ς

−

l2

ϱ2 1

)

>

0

and

λ

min

(

2

K

1

−

(4 +

ϱ

21

)

I

)

>

0

. Then the following theorem is

obtained.

Theorem 2:

For robotic system (1), by designing adaptive

neural network controller (30) with adaptive law (32), the

controller can ensure that all the error signals are UUB.

Fur-thermore,

z

1

eventually converges to the compact set defined

as

Ω

z1

:=

{

z

1

∈

R

n

||

z

1i

| ≤

√

2

e

H2

, i

= 1

, . . . , n

}

, and

z

2

eventually converges to the compact set defined as

Ω

z2

:=

{

z

2

∈

R

n

|||

z

2

|| ≤

√

2H2

λmin(M)

}

, where

H

2

=

V

2

(0) +

C_κ₂2

.

Proof

: The proof is similar to that of Theorem 1, so it will

not be discussed in details.

C. Output-Feedback-Based Adaptive Neural Control Design

Assume that velocity signal

x

2

is immeasurable. We will

introduce a high-gain observer to estimate

x

2

.

x

2

is estimated

by

x

ˆ

2

=

π_ρ2

. Estimate error is defined as

z

˜

2

=

π_ρ2

−

x

2

and is

said to be bounded [73], i.e.,

∥

z

˜

2

∥ ≤

z

¯

with

z

¯

being a positive

constant. Dynamics of

π

2

is given as

ρ

π

˙

1

=

π

2

,

(41)

ρ

π

˙

2

=

−

λ

1

π

2

−

π

2

+

x

1

(42)

where

λ

1

is a constant satisfying that

λ

1

s

+ 1

is Hurwitz, and

ρ

is a number. An adaptive neural controller is designed as

µ

=

−

tanh(

z

1

)

−

K

1

tanh(ˆ

z

2

) +

B

tanh(

B

−1

ψ

ˆ

)

(43)

ˆ

ψ

= ˆ

θ

T

φ

( ˆ

Z

)

(44)

˙ˆ

θ

i

=

−

Γ

i

(

φ

( ˆ

Z

)ˆ

z

2i

+

ς

θ

ˆ

i

)

, i

= 1

, . . . , n

(45)

where

K

1

= diag[

k

11

, . . . , k

1n

]

∈

R

n×n

is a positive definite

matrix,

Z

ˆ

= [

x

T1

,

x

ˆ

T2

, z

T1

,

z

ˆ

2T

]

T

∈

R

4n

,

z

ˆ

2

=

π_ρ2

−

α

,

B

=

diag[

δ

i

µ

+i

+ (1

−

δ

i

)

µ

−i

]

∈

R

n_×n

with

δ

i

defined as

δ

i

=

{

1

if ˆ

θ

T

i

φ

( ˆ

Z

)

≥

β

i

0

Otherwise

,

(46)

and

β

i

= ˆ

θ

iT

γφ

¯

+

ℓ

i

with

ℓ

i

defined in (33),

i

= 1

, . . . , n

.

Remark 3:

A difference from switching function

δ

i

in (33)

is that velocity signal

x

2

in this section is estimated by a

high-gain observer. Thus the switching function

δ

i

in (33) should

be redesigned. According to (8), we can obtain

θ

ˆ

T

i

φ

(

Z

) =

ˆ

θ

T

i

φ

( ˆ

Z

)

−

θ

ˆ

Ti

γφ

¯

. Consider (8) and (33), we know that if

δ

i

= 1

, it follows that

θ

ˆ

Ti

φ

(

Z

) = ˆ

θ

T

i

φ

( ˆ

Z

)

−

θ

ˆ

T

i

γφ

¯

≥

ℓ

i

and

θ

ˆ

T

i

φ

( ˆ

Z

)

≥

θ

ˆ

Ti

¯

γφ

+

ℓ

i

, and if

δ

i

= 0

, it follows that

ˆ

θ

T

i

φ

(

Z

) = ˆ

θ

iT

φ

( ˆ

Z

)

−

θ

ˆ

iT

γφ < ℓ

¯

i

and

θ

ˆ

Ti

φ

( ˆ

Z

)

<

θ

ˆ

Ti

¯

γφ

+

ℓ

i

.

Defining

β

i

= ˆ

θ

iT

γφ

¯

+

ℓ

i

, we can obtain the switching function

δ

i

in (46),

i

= 1

, . . . , n

.

Similar to analysis in Remark 1, we can conclude that

µ

i

, i

=

1

, . . . , n

given in (43) are bounded, i.e.,

µ

−_ci

≤

µ

i

≤

µ

+ci

, i

=

1

, . . . , n

, are guaranteed. A Lyapunov function candidate is

chosen as

V

3

=

n

∑

i=1

ln(cosh(

z

1i

)) +

1

2

z

T

2

M z

2

+

1

2

n

∑

i=1

˜

(6)

Substituting (43)-(45) into the time derivative of (47), we

further have

˙

V

3

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

n

∑

i=1

˜

θ

_iT

(

φ

( ˆ

Z

)ˆ

z

2i

+

ς

θ

ˆ

i

)

−

z

T₂

K

1

tanh(ˆ

z

2

) +

z

2T

(

B

tanh(

B

−

1

ψ

ˆ

)

−

B

tanh(

B

−1

ψ

)

−

p

(

µ

))

(48)

Similar

with

calculation

in

III-B,

B

tanh(

B

−1

ψ

ˆ

)

−

B

tanh(

B

−1

ψ

)

can be simplified as

B

i

tanh(

B

i−1

ψ

ˆ

i

)

−

B

i

tanh(

B

i−1

ψ

i

)

=

(1

−

tanh

2

(

η

i

))( ˆ

ψ

i

−

ψ

i

)

, where

η

i

∈

(

B

i−1

ψ

ˆ

i

, B

−i 1

ψ

i

)

or

η

i

∈

(

B

i−1

ψ

i

, B

i−1

ψ

ˆ

i

)

.

With

combination

of

(8),

(29)

and

(44),

we

have

ˆ

ψ

i

−

ψ

i

= ˜

θ

Ti

φ

(

Z

) + ˜

θ

T

i

¯

γφ

+

θ

T

i

γφ

¯

+

ϵ

i

(

Z

)

,

i

= 1

, . . . , n

.

According to Taylor expansion, we know

tanh(ˆ

z

2

) = ˆ

z

2

+

o

(ˆ

z

2

)

,

∥

z

ˆ

2

∥

<

π

2

(49)

where

o

(ˆ

z

2

) =

−

1₃

z

ˆ

32

+

152

ˆ

z

5 2

−

31517

z

ˆ

7

2

+

· · ·

, and in the interval

∥

z

ˆ

2

∥

<

π₂

,

o

(ˆ

z

2

)

is bounded, i.e.,

∥

o

(ˆ

z

2

)

∥ ≤

¯

o

c

with

¯

o

c

being

a positive constant. Thus, (48) becomes

˙

V

3

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

n

∑

i=1

˜

θ

_iT

(

φ

( ˆ

Z

)ˆ

z

2i

+

ς

θ

ˆ

i

)

−

z

T₂

K

1

z

ˆ

2

−

z

2T

K

1

o

(ˆ

z

2

) +

z

2T

(

I

−

Tanh

2

(

η

))

×

(˜

θ

T

φ

(

Z

) + ˜

θ

T

γφ

¯

+

θ

T

¯

γφ

+

ϵ

(

Z

))

−

z

₂T

p

(

µ

)

(50)

Note that

˜

z

2

=

π

2

ρ

−

x

2

= ˆ

x

2

−

x

2

= (ˆ

x

2

−

α

)

−

(

x

2

−

α

) = ˆ

z

2

−

z

2

(51)

Thus,

we

have

−

∑

n_i₌₁

θ

˜

T

i

φ

( ˆ

Z

)ˆ

z

2i

+

z

T2

θ

˜

T

φ

(

Z

)

=

−

∑

n i=1

θ

˜

T

i

(

φ

( ˆ

Z

)ˆ

z

2i

−

φ

(

Z

)

z

2i

)

. Since

φ

( ˆ

Z

) =

φ

(

Z

) + ¯

γφ

,

we have

−

n

∑

i=1

˜

θ

T_i

φ

( ˆ

Z

)ˆ

z

2i

+

z

2T

θ

˜

T

φ

(

Z

)

=

−

n

∑

i=1

˜

θ

_iT

(

φ

(

Z

)ˆ

z

2i

+ ¯

γφ

z

ˆ

2i

−

φ

(

Z

)

z

2i

)

=

−

n

∑

i=1

˜

θ

T_i

(

φ

(

Z

)˜

z

2i

+ ¯

γφz

2i

+ ¯

γφ

z

˜

2i

)

(52)

Thus, we have

˙

V

3

=

−

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

z

2T

K

1

z

2

−

n

∑

i=1

˜

θ

T_i

ς

θ

ˆ

i

−

z

T2

K

1

z

˜

2

−

z

2T

K

1

o

(ˆ

z

2

)

−

n

∑

i=1

˜

θ

iT

(

φ

(

Z

)˜

z

2i

+ ¯

γφz

2i

+ ¯

γφ

z

˜

2i

) + 2

|

z

T2

(˜

θ

T

γφ

¯

+

θ

T

¯

γφ

+

ϵ

(

Z

))

|

+

|

z

₂T

θ

˜

T

φ

(

Z

)

| −

z

₂T

p

(

µ

)

(53)

In terms of Young’s inequality, we have

−

z

T

2

p

(

µ

)

≤

1

2

z

T

2

z

2

+

1₂

p

¯

2

,

−

∑

n i=1

θ

˜

T

i

ς

θ

ˆ

i

≤

−

ς₂

∑

n i=1

θ

˜

T

i

θ

˜

i

+

ς

2

∑

n

i=1

θ

T

i

θ

i

,

−

z

2T

K

1

z

˜

2

≤

1₂

z

2T

z

2

+

1₂

λ

max

(

K

1T

K

1

)¯

z

2

,

z

T

2

K

1

o

(ˆ

z

2

)

≤

1₂

z

2T

z

2

+

1₂

λ

max

(

K

1T

K

1

)¯

o

2c

,

−

∑

n i=1

θ

˜

T

i

φ

(

Z

)˜

z

2i

≤

ϱ2₂

2

∑

n i=1

θ

˜

T

i

θ

˜

i

+

₂1_ϱ2

2

l

2

¯

z

2

,

−

∑

n

i=1

θ

˜

T

i

γφz

¯

2i

≤

ϱ

2 3

2

∑

n i=1

θ

˜

T

i

θ

˜

i

+

¯γ

2_∥_φ_∥2

2ϱ2 3

z

T

2

z

2

,

−

∑

n

i=1

θ

˜

iT

γφ

¯

z

˜

2i

≤

ϱ2 4

2

∑

n

i=1

θ

˜

iT

θ

˜

i

+

¯γ

2_∥_φ_∥2

2ϱ2 4

¯

z

2

,

|

z

2T

θ

˜

T

φ

(

Z

)

| ≤

ϱ2 5

2

∑

n i=1

θ

˜

T

i

θ

˜

i

+

l

2

2ϱ2 5

z

2T

z

2

,

|

z

2T

θ

˜

T

¯

γφ

| ≤

ϱ2₃

2

∑

n i=1

θ

˜

T

i

θ

˜

i

+

¯

γ2_∥_φ_∥2

2ϱ2 3

z

T

2

z

2

,

|

z

2T

θ

T

γφ

¯

| ≤

ϱ2₃

2

∑

n

i=1

θ

T

i

θ

i

+

¯

γ2∥φ∥2

2ϱ2 3

z

₂T

z

2

, and

|

z

2T

ϵ

(

Z

)

| ≤

1 2

z

T

2

z

2

+

1₂

ϵ

¯

2

. Therefore, we

have

˙

V

3

≤ −

n

∑

i=1

k

i

ln(cosh(

z

1i

))

−

z

2T

(

K

1

−

1

2

(5 + ¯

γ

2

∥

φ

∥

2

×

5

ϱ

2 3

+

l

2

ϱ

2 5

)

I

)

z

2

−

1

2

(

ς

−

ϱ

2 2

−

3

ϱ

2 3

−

ϱ

2 4

−

ϱ

2 5

)

n

∑

i=1

˜

θ

_iT

θ

˜

i

+

1

2

(

ς

+ 2

ϱ

2 3

)

n

∑

i=1

θ

_iT

θ

i

+

1

2

(

l

2

ϱ

2 2

+

¯

γ

2

∥

φ

∥

2

ϱ

2

4

+

λ

max

(

K

1T

K

1

)

¯

z

2

+

1

2

λ

max

(

K

T

1

K

1

)¯

o

2c

+ ¯

ϵ

2

+

1

2

p

¯

2

≤ −

κ

3

V

3

+

C

3

(54)

where

κ

3

= min

{

min

i=1,...,n

k

i

,

λ

min

(

2

K

1

−

(5 +

5¯γ

2_∥_φ_∥2

ϱ2 3

+

_ϱl22 5

)

I

)

λ

max

(

M

)

min

i=1,...,n

(

ς

−

ϱ

22

−

3

ϱ

32

−

ϱ

24

−

ϱ

25

)

λ

max

(Γ

−i1

)

)}

C

3

=

1

2

(

ς

+ 2

ϱ

2 3

)

n

∑

i=1

θ

iT

θ

i

+

1

2

λ

max

(

K

T

1

K

1

)¯

o

2c

+ ¯

ϵ

2

+

1

2

(

l

2

ϱ

2 2

+

γ

¯

2

∥

φ

∥

2

ϱ

2

4

+

λ

max

(

K

1T

K

1

)

¯

z

2

+

1

2

p

¯

2

(55)

To guarantee

κ

3

>

0

, controller parameters should be

chosen to satisfy:

min

i=1,...,n

k

i

>

0

,

λ

min

(

2

K

1

−

(5 +

5¯γ2_∥_φ_∥2

ϱ2 3

+

_ϱl22 5

)

I

)

>

0

and

(

ς

−

ϱ

22

−

3

ϱ

32

−

ϱ

24

−

ϱ

25

)

>

0

,

where

ϱ

2

,

ϱ

3

,

ϱ

4

and

ϱ

5

are adjustable positive parameters.

Then the following theorem is obtained.

Theorem 3:

For robotic system (1), by designing

adap-tive neural network controller (43) with adapadap-tive law (45)

and state observer (42), the controller can ensure that

all the error signals are UUB. Furthermore,

z

1

eventu-ally converges to the compact set defined as

Ω

z1

:=

{

z

1

∈

R

n

||

z

1i

| ≤

√

2

e

H3

, i

= 1

, . . . , n

}

, and

z

2

eventual-ly converges to the compact set defined as

Ω

z2

:=

{

z

2

∈

R

n

|||

z

2

|| ≤

√

2H3

λmin(M)

}

, where

H

3

=

V

3

(0) +

C_κ3

3

.

Proof

: The proof is similar to that of Theorem 1, so it will

not be discussed in details.

IV. S

IMULATION

(7)

system matrixes of the robot given in (1) are given by

M

=

[

M

11

M

12

M

13

M

21

M

22

M

23

M

31

M

32

M

33

]

(56)

C

=





C

1121

C

1222

C

1323

C

31

C

32

C

33





, G

=





G

12

G

3





(57)

where

M

11

=

m

3

q

32

sin

2

(

q

2

)+

p

1

;

D

12

=

p

2

q

3

cos(

q

2

);

M

13

=

p

2

sin(

q

2

);

M

21

=

p

2

q

3

cos(

q

2

);

M

22

=

m

3

q

23

+

I

2

;

M

23

=

0;

M

31

=

p

2

sin(

q

2

);

M

32

= 0;

M

33

=

m

3

;

C

11

=

p

4

q

˙

2

+

p

5

q

˙

3

;

C

12

=

p

4

q

˙

1

−

p

3

q

3

p

8

;

C

13

=

p

5

q

˙

1

−

p

3

p

6

q

3

;

C

21

=

−

p

4

q

˙

1

;

C

22

=

m

3

q

3

q

˙

3

;

C

23

=

p

3

p

9

−

m

3

q

3

q

˙

2

;

C

31

=

−

p

5

q

˙

1

+

p

3

p

10

;

C

32

=

m

3

q

3

q

˙

2

+

p

3

p

11

;

C

33

= 0;

G

1

= 0;

G

2

=

−

m

3

gq

3

cos(

q

2

);

G

3

=

−

m

3

g

sin(

q

2

)

.

where

p

1

=

m

3

l

22

+

m

2

l

21

+

I

1

;

p

2

=

m

3

l

2

;

p

3

=

m

3

l

1

;

p

4

=

m

3

q

32

sin(

q

2

) cos(

q

2

)

;

p

5

=

m

3

q

32

sin

2

(

q

2

)

;

p

6

= sin(

q

2

) ˙

q

2

;

p

7

= sin(

q

2

) ˙

q

3

;

p

8

=

p

6

+

p

7

;

p

9

= cos(

q

2

) ˙

q

1

;

p

10

= cos(

q

2

) ˙

q

2

and

p

11

= cos(

q

2

) ˙

q

3

. Parameters of the robotic system are defined

[image:7.612.354.520.60.192.2] [image:7.612.350.522.244.373.2]

in the table below.

Table 1: Parameters of the robot

Parameter

Description

Value

m

1

Mass of link

1

2

.

00

kg

m

2

Mass of link

2

1

.

00

kg

m

3

Mass of link

3

0

.

30

kg

l

1

Length of link

1

.

00

m

l

2

Length of link

2

0

.

20

m

l

3

Length of link

3

1

.

00

m

I

1

Inertia of link

1

0

.

5

×

10

−3

kgm

2

I

2

Inertia of link

2

0

.

1

×

10

−3

kgm

2

The detailed simulation results are given as follows.

A. Model-based Control Simulation Implementation

In this section, the effectiveness of model-based control (23)

will be verified by simulation implementation. Initial values

are set as:

x

1

(0) = [0

.

05

,

0

.

56

,

−

0

.

05]

T

rad and

x

2

(0) =

[0

,

0

,

0]

T

rad/s. Controller parameters are chosen as follows:

K

= diag[100

,

100

,

100]

,

K

1

= diag[10

,

10

,

10]

,

µ

+1

= 1

,

µ

+₂

= 2

,

µ

+₃

= 2

,

µ

−₁

=

−

2

,

µ

−₂

=

−

1

and

µ

−₃

=

−

2

.

Therefore observing (23), we know

−

13

N m

≤

µ

1

≤

12

N m

(58)

−

12

N m

≤

µ

2

≤

13

N m

(59)

−

13

N m

≤

µ

3

≤

13

N m

(60)

The

reference

trajectory

of

x

1

is

set

as

x

d

=

[0

.

5 sin(

t

)

,

0

.

6 cos(

t

)

,

0

.

7 sin(

t

)]

T

rad.

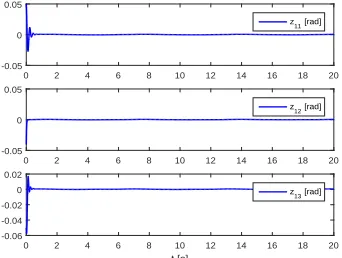
The detailed simulation results are given in Figs. 1-3. In Fig.

1, actual trajectory

x

1

and reference trajectory

x

d

are plotted,

respectively, and Fig. 1 also illustrates that

x

1

fast converges to

a small neighborhood of reference trajectory

x

d

, which shows

that the tracking performance of the robot is satisfactory. In

Fig. 2, tracking error

z

1

is plotted, and it can be known that

z

1

converges to a small neighborhood of zero with a satisfactory

overshoot. In Fig. 3, control input

µ

is given and is constrained

in the predefined region, i.e.,

µ

−_ci

≤

µ

i

≤

µ

+ci

,

i

= 1

,

2

,

3

, are

satisfied.

0 2 4 6 8 10 12 14 16 18 20

-1 0 1

xd1 [rad]

x11 [rad]

0 2 4 6 8 10 12 14 16 18 20

-1 0 1

xd2 [rad]

x12 [rad]

0 2 4 6 8 10 12 14 16 18 20

t [s] -1

0 1

xd3 [rad]

x

13 [rad]

Fig. 1. Actual trajectoryx1and reference trajectoryxdunder model-based

control (23).

0 2 4 6 8 10 12 14 16 18 20

-0.05 0 0.05

z

11 [rad]

0 2 4 6 8 10 12 14 16 18 20

-0.05 0 0.05

z12 [rad]

0 2 4 6 8 10 12 14 16 18 20

t [s] -0.06

-0.04 -0.02 0 0.02

z13 [rad]

Fig. 2. Tracking errorz1=x1−xdunder model-based control (23).

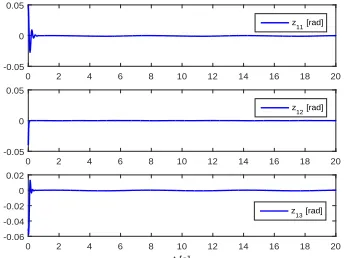
B. State-Feedback-Based Adaptive Neural Control Simulation

Implementation

In this section, the effectiveness of proposed control (30)

will be verified by simulation implementation. The number of

neural nodes is set as

l

= 2

12

, the center of activation function

ψ

(

Z

)

is chosen in the area of

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

×

[

−

1

,

1]

. The width of centers is set as

η

2

= 1

. Initial

values are set as

θ

ˆ

1

(0) = ˆ

θ

2

(0) = ˆ

θ

3

(0) = [0

, . . . ,

0]

T

∈

R

212

. The parameters of the updating law given in (32) are

set as

Γ

1

= diag[100

,

100

,

100]

,

Γ

2

= diag[50

,

50

,

50]

,

Γ

3

=

diag[100

,

100

,

100]

and

ς

= 0

.

0001

. The rest of controller

parameters are the same as those of section IV-A.

The detailed simulation results are given in Figs. 4-7. In

Fig. 4, actual trajectory

x

1

x

d

are

plotted, respectively, and Fig. 4 shows that

x

1

converges to a

small neighborhood of reference trajectory

x

d

, which shows

that the tracking performance of the robot is satisfactory. In

Fig. 5, tracking error

z

1

is given. Fig. 6 plots control input

µ

and furthermore

µ

is constrained in the the predefined region,

i.e.,

µ

−_ci

≤

µ

i

≤

µ

+ci

,

i

= 1

,

2

,

3

, are satisfied. Fig. 7 gives the

Euclidean norm of weight vector

θ

ˆ

i

,

i

= 1

,

2

,

3

. By observing

[image:7.612.60.287.300.417.2]

(8)

0 2 4 6 8 10 12 14 16 18 20 -20

0 20

Input

µ

1

[Nm] µ

1

µ+c1

µ

-c1

0 2 4 6 8 10 12 14 16 18 20

-20 0 20

Input

µ

2

[Nm] µ

2

µ+

c2

µ-c2

0 2 4 6 8 10 12 14 16 18 20

t [s] -20

0 20

Input

µ3

[Nm] µ3

µ+

c3

[image:8.612.347.522.59.193.2]

µ-c3

Fig. 3. Control inputµunder model-based control (23).

0 2 4 6 8 10 12 14 16 18 20

-1 0 1

xd1 [rad]

x11 [rad]

0 2 4 6 8 10 12 14 16 18 20

-1 0 1

xd2 [rad]

x

12 [rad]

0 2 4 6 8 10 12 14 16 18 20

t [s] -1

0 1

xd3 [rad]

[image:8.612.84.259.60.194.2]

x13 [rad]

Fig. 4. Actual trajectoryx1and reference trajectoryxdunder

state-feedback-based adaptive neural control (30).

C. Output-Feedback-Based Adaptive Neural Control

Simula-tion ImplementaSimula-tion

In this section, the effectiveness of proposed control (43)

will be verified by simulation implementation. High-gain

ob-server parameters are set as

λ

1

= 1

and

ρ

= 0

.

0007

. The rest

of controller parameters are the same as those of section IV-B.

The detailed simulation results are given in Figs. 8-11.

In Fig. 8, actual trajectory

x

1

x

d

are plotted, respectively, and Fig. 8 also illustrates that

x

1

converges to a small neighborhood of reference trajectory

0 2 4 6 8 10 12 14 16 18 20

-0.05 0 0.05

z11 [rad]

0 2 4 6 8 10 12 14 16 18 20

-0.05 0 0.05

z12 [rad]

0 2 4 6 8 10 12 14 16 18 20

t [s] -0.06

-0.04 -0.02 0 0.02

z13 [rad]

Fig. 5. Tracking errorz1=x1−xdunder state-feedback-based adaptive

neural control (30).

0 2 4 6 8 10 12 14 16 18 20

-20 0 20

Input

µ

1

[Nm] µ

1

µ+c1

µ

-c1

0