Extracting k Most Important Groups from Data Efficiently
Full text
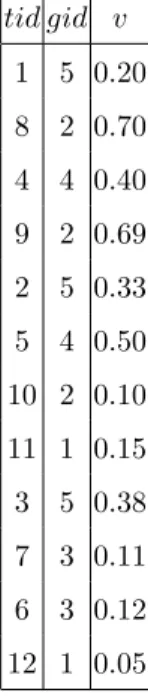
Figure




Related documents
To address this gap, we conducted a longitudinal ana- lysis in the National Social Life, Health and Aging Pro- ject (NSHAP) to examine the association between greenness
Standardization of herbal raw drugs include passport data of raw plant drugs, botanical authentification, microscopic & molecular examination, identification of
Field experiments were conducted at Ebonyi State University Research Farm during 2009 and 2010 farming seasons to evaluate the effect of intercropping maize with
The Ociesęki Formation ranges from the lowermost Holmia − Schmidtiellus Assemblage Zone through the Protolenus − Issafeniella Zone of Cam- brian Series 2 up to the
In crime fiction TV series (as well as other types of crime fiction) crime scenes are reconstructed and interpreted by the investigators through narrative and
19% serve a county. Fourteen per cent of the centers provide service for adjoining states in addition to the states in which they are located; usually these adjoining states have
Como o prop´osito ´e identificar o n´ıvel de vulnerabilidade de 100% das fam´ılias inseridas no IRSAS, foram escolhidos atributos comuns a todas as fam´ılias cadastradas