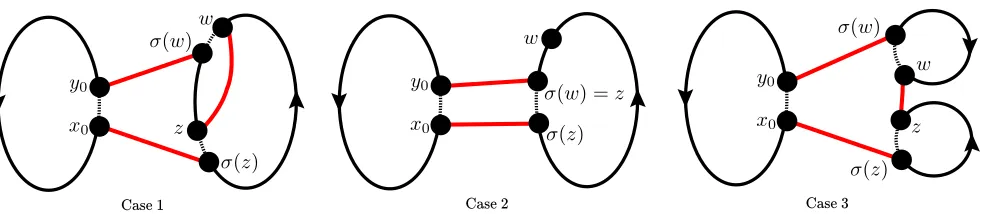
Decompositions into spanning rainbow structures
Full text
Figure
Related documents
If dirty pages are often evicted from the buffer pool after undertaking only a few updates, then IPL will end up with performing too many page writes only to write a small number of
Goal: To provide a staff development process to help teachers infuse higher order thinking skills and multicultural concepts into existing curriculum for all students and to
If the real system behaves anything like these model results, major increases in market efficiency can be had by a combination of: (1) reducing planning and construction lags;
It also shows that there is a need to assemble further (and more accurate) data regarding the actual cost premium of green or sustainably designed buildings, as well as data
The result of the research showed that students who were taught by using stirred word game had better achievement in learning vocabulary than those who were taught by
Production Power distributor Hydroelectric power plant Wind turbines Solar panels Management Local or remote acces PLC source management Energy efficiency cabinet Batteries
Property Facilities: 2 restaurants • 3 bars • 2 pools • pool with swim-up bar • health spa centre • tour desk • parking • shop Accommodation: 209 rooms • air-conditioning • mini
Gutzwiller, Michael (2009) "The Need for Research on Child and Adolescent Group Practices for Male Gender Role Strain," Graduate Journal of Counseling Psychology : Vol..