© 2012 Tadbir Operational Research Group Ltd. All rights reserved. www.tadbir.ca
ISSN 1735-8523 (Print), ISSN 1927-0089 (Online)
Using a genetic algorithm to optimize the total
cost for a location-routing-inventory problem
in a supply chain with risk pooling
Fatemeh Forouzanfar 1 and Reza Tavakkoli-Moghaddam 2,* 1 South Tehran Branch, Islamic Azad University, Tehran, Iran 2 College of Engineering, University of Tehran, Tehran, Iran
Abstract. This paper addresses a problem of designing a multi-echelon supply chain with the single sourcing type and the related inventory systems. We also presents a novel mathematical model considering the risk-pooling, lead time, multi-echelon inventory under the demand uncertainty, routing of vehicles from distribution centers (DCs) to customers in order to give services in a stochastic supply chain system, simultaneously. This problem is formulated as a mix integer non-linear programming model. The aim of this model is to determine, the number of the located distribution centers, their locations and capacity levels, to allocate customers to distribution centers and distribution centers to suppliers optimally. In addition, it is also to determine the net lead time of distribution centers and the inventory control decisions. In addition, it is to determine the service time of every distribution centers and routing decisions. All these are done in a way that the total system cost is minimized. The GAMS software is used to solve the presented model for small-size problems. The given problem belongs to the class of NP-hard ones. Hence, to solve the large-sized instances, a genetic algorithm is used. The sensitivity analysis has been performed to investigate the impact of effective parameters on the final solutions.
Keywords: supply chain; inventory control; risk-pooling; uncertainty; capacity levels
* Received October 2011. Accepted January 2012
Introduction
Nowadays, the competition in business environment is increasing considerably. The life cycle of products is becoming shorter, customer demands are getting more uncertain, and the lead time on their service is getting very effective. The demand’s variety can be recognized as one of the important sources of uncertainty in a supply chain (Gupta et al. 2000; Park et al. 2010). Risk pooling is a strategy to redesign the supply chain, the production process or the product to either reduce the uncertainty the firm faces or hedge uncertainty so that the firm is in a better position to mitigate the consequence of uncertainty. The proposed risk-pooling strategy and centralizing the inventory at distribution centers are considered as one of the effective ways to manage such a demand uncertainty for achieving appropriate service levels to customers. Due to the increasing pressure for remaining competition in the global market place, optimizing inventories across the supply chain has become a major challenge for the process of industries to reduce the costs and improve the customer service. This challenge requires integrating inventory management in a supply chain network design (You and Grossmann, 2009). The lead time is one of the effective
* Correspondence:Reza Tavakkoli-Moghaddam, Department of Industrial Engineering, College of Engineering, University of Tehran, P.O. Box 11155-4563 Tehran, Iran. E-mail: tavakoli@ut.ac.ir
factors in the safety stock levels due to the customer demand uncertainty (Park et al. 2010). Surely, the lower level for product, is considered as an additional value that can gain a long term or short term competitive benefit in the market. In the recent decades, the topic of multi-depot heterogeneous vehicle routing problem (MDHVRP) is proposed to increase the productivity and efficiency of transportation systems, in which this model leads to the least cost function by minimizing the number of vehicles (Bettinelli et al. 2011).
One of the important factors of the total productivity and profitability of a supply chain is to consider its distribution network, which can be used to achieve the various supply chain objectives. Designing a distribution network consists of three sub-problems; namely, location-allocation, vehicle routing, and inventory control. In the literature, there are some research studies amalgamating two of the above sub-problems, such as location-routing, inventory-routing, and location-inventory problems (Ahmadi Javid and Azad, 2010). These three sub-problems of a distribution network design are considered in few papers simultaneously. However, in this paper for the first time, we present a model to concurrently optimize the location, allocation, capacity, lead time, inventory, and routing decisions with risk-pooling in a stochastic supply chain system. Location-routing-inventory problems are laid in the non-deterministic polynomial-hard category, due to the intrinsic complexity of calculations. Therefore, solving large-sized problems is not possible by linear programming using ordinary operational research software in a reasonable time. A genetic algorithm (GA) has unique characteristics compared to other meta-heuristic methods. The following advantages have been added in the revised paper (Goldberge, 1989).
A genetic algorithm (GA) works with the coding of the parameter set, not the parameters themselves.
It is a population-based solution, not a single point.
It uses probabilistic transition rules, not deterministic rules.
It trades-off between exploration and exploitation.
It works on the number of variables at the same time.
It is capable of working with any kinds of the objective functions and constraints in linear and/or non-linear forms within any solution space (discrete or continuous).
Consequently, it is applied in this paper with respect to the model complexity. It is a bio-inspired algorithm taken from the nature and it is also one of the most popular meta-heuristics, which is applied in many optimization problems with different functions. The previous information is derived and used in searching for promising solutions within the solution space. Furthermore, it has been utilized for solving supply chain problems extensively. For further study, readers may refer to Wang et al. 2011; Kannan et al. 2010; Yun et al. 2009; Zegordi et al. 2010 and Chang et al. 2010.
Problem formulation
The mathematical model of the considered problem, minimizes the fixed cost of locating the opened distribution centers, the safety stock costs of distribution center by considering uncertainty in customer’s demand, inventory ordering and holding costs and also vehicles routing beginning from a distribution center (DC) with the aim of replying and covering to the devoted customer’s demands to that DC by considering the risk-pooling. The important assumptions in this paper are as follows.
1) One kind of product is involved (Paksoy and Chang, 2010).
2) Each distribution center j is assumed to follow a (Qi, Rj) inventory policy (Ahmadi Javid and Azad, 2010).
3) A single sourcing strategy is considered in the whole supply chain (Park et al., 2010).
4) It is considered that the customers’ demands after reaching to retailer are independent and follows a normal distribution (Park et al., 2010; Ahmadi Javid and Azad, 2010).
5) Each plant can give any kinds of services in any amount of demands to the related devoted distribution
centers. 6) We consider different capacity levels for each distribution center, and finally one capacity for each of
them is selected.
7) Each DC with the limited capacity carries on-hand inventory to satisfy demands from customer demand zones as well as safety stock to deal with the mutability of the customer demands at customer demand zones to attain risk-pooling profits (Park et al., 2010).
8) All customers must be served.
9) The number of available vehicles for each type and the number of allowed routes for each DC are limited (Bettinelli et al., 2011)
10)To determine all the feasible routes, the following factors are taken into account: - Each customer must be visited by only one vehicle.
- Each route begins at a DC and ends at the same DC.
- The sum of the demands of the customers served in each route must not exceed the capacity of the associated vehicle.
- Each of the distribution centers and the vehicles has the various, limited and determined capacity (Bettinelli et al., 2011; Marinakis and Marinaki, 2010).
Model formulation
Following are the notations introduced for the mathematical description of the proposed model.
Indices
I Set of plants indexed by i
J Set of candidate DC locations indexed by j K Set of customer demand zones indexed by k Nj Set of capacity levels available to DCj (jJ)
V Set of vehicles
jv
Set of all feasible routes using a vehicle of type v (v ∊V) from DCj (jJ)
Parameters n j
F
Yearly fixed cost for opening and operating distribution center j with capacity level n(nNj,jJ) j
Safety stock factor of DCj (jJ)j
h
Unit inventory holding cost at DCj (jJ), (annually)
k
Mean demand at customer demand zone k k2
Variance of demand at customer demand zone k jA Fixed inventory ordering cost at DCj
n j
b
Capacity with level n for DCj
ij
t
Order processing time of DCj if it is served by plant i; including material handling time of DCj, transportation time from plant i to DCj, and inventory review period.
i
S
Service time of plant i rC Cost of each demand unit in route r (these costs include the fixed cost of vehicle plus the transportation cost of each demand unit in route r. the mentioned transportation cost for each demand unit is not related to customer demand zone and it is considered fixed for all locations in each route r.
v
Number of available vehicles of each type v jg Number of routes associated with each distribution center j
Binary coefficients
Decision variables j
n
U
1 if distribution center j is opened with capacity level n; and 0, otherwiseji
X
1 if distribution center j is served by plant i; and 0, otherwise
jk
Z 1 if customer k is assigned to distribution center j; and 0, otherwise
r
X 1 if and only if route r is selected; and 0, otherwise
j
L
Net lead time of DCj
j
Service time of DCjj
Q Order size at distribution center j
The problem formulation is as follows.
Minimize 2
2
j n n k jk j j j ji j j j j j k jk j J n N j J k K i I j J k K j ji i I j JZ A
h Q X
F U
h
L
Z
Q X
jv k kr r r j J v V k K rP X C
s.t. 1
Nj n n j U J j (1)
j N n n j n j K k jk kZ b U
J j (2) n j n N n j K k jk k j j I i ji jX L Z b U Q j
2 J j (3) j ji ij I i i jS
t
X
L
)
(
J j (4)
j N n n j I i ji U X J j (5) 1
J j jk ZK
k
(6)1
I i jiX
J j (7) jk N n n j Z U j
J j ,
k
K
(8) jk I i jiZ
X
J j ,
k
K
(9) 1
J j vVr r kr jv X PK
k
(10)v J j r r jv
X
V
v
(11)
V v r r jvX
gj jJ (12)
V v r k K r kr jk jvX
P
Z
1
J j (13)
0,1 n j U jJ,nNj
0,1 ji X jJ,iI
0,1 jk Z jJ,kK
0,1 r X
V v J j jv r , (14) 0 j L jJ 0 j
jJ 0 j Q jJ (15)This model minimizes the total expected cost consisting of the fixed cost for opening distribution centers with a certain capacity level, the expected annual inventory cost, and the annual routing cost. Constraint (1) ensures that each distribution center can be assigned to only one capacity level. Constraints (2) and (3) are the capacity constraints associated with the distribution centers. Constraint (4) imposes limits on the minimum amount of net lead time of DCj. Constraints (5) states that if the distribution center j with n capacity is opened, it is serviced by a plant. Constraints (6) and (7) represent the single-sourcing constraints for each customer demand zone and each DC, respectively. Constraint (8) ensures that if the distribution center j is allocated to the customer k, that center should certainly be established by a determined capacity level. Constraint (9) makes sure that if the distribution center j gives the service to the customer k, that center must get services from a plant. Constraint (10) is standard set covering constraints, modeling assumption 6. Constraints (11) and (12) impose limits on the maximum number of available vehicles of each type and maximum number of permitted routes for each DC, modeling assumption 7. Constraint (13) implies that there is at least one customer in one selected route. Constraint (14) enforces the integrality restrictions on the binary variables. Finally, Constraint (15) enforces the non-negativity restrictions on the other decision variables.
Solution methodology
Some different small-sized problems have been solved by the conventional branch-and-bound imbedded in the GAMS (General Algebraic Modeling System) software in order to consider the feasibility and validity of the presented mathematical model in small-sized problems. To solve large-sized problems, a genetic algorithm (GA) is proposed.
Chromosome definition
It is obvious that the solution representation is the base of any meta-heuristic approach. Four one-dimensional matrices are used to demonstrate the solution. The first matrix is the 1×m one (m is the number of the distribution centers) and denotes that each distribution center is established with its capacity levels. Each arrayof the matrix is corresponding to a number between 1 and Nj, as shown in Figure 1.
Njm ….
Nj3
Nj2
Nj1
The second matrix is the 1×m and represents the assignment of the distribution centers to the plants. Eacharray of the matrix is associated with a number between 1 and n (n is the number of plants) as shown in Figure 2.
Im ….
I3
I2
I1
Fig. 2. Presentation the second matrix
The third matrix is the 1×k one (k is the number of the customers) that shows the customers allocation to the distributors. The associatedarrays are determined by a number between 1 and m, as shown in Figure 3.
Jk ….
J3
J2
J1
Fig. 3. Presentation of the third matrix
The fourth matrix is the 1×r one (r is the number of the routes) that shows the selected routes, as shown in Figure 4. Eacharray of the matrix belongs to the numbers 0 or 1. It can be understood that the given route has been used if the i-th cell of the matrix is 1; otherwise, it is 0.
Ar ….
A3
A2
A1
Fig. 4. Presentation of the fourth matrix Establishing an initial population
The first step is to generate an initialpopulation from the chromosomes once so that each one indicates to a specific solution. The required feasible solutions are generated randomly in this section.
Fitness function
The fitness function is similar to considered objective function. As the chromosomes are formed and modified, the objective function value is calculated for each one to justify it.
Sampling mechanism
The sampling mechanism pertains how the chromosomes are chosen with respect to the sampling space. The bi-tournament approach is applied in this paper, in which the best solution is selected from the population and then the next optimal solution is selected from the rest.
Crossover operator
In this paper, we use a two-point crossover operator for all the four matrices. However, it should be noted that the obtained solutions from the crossover operator may be infeasible. Thus, they must be transformed into feasible solutions by modifying practices. In this operator, two random indices are generated in the interval of 1 and the length of the matrix for each one. The first and second offspring are also generated as follows.
The first part of the first parent + the second part of the second parent + the third part of the first parent.
The first part of the second parent + the second part of the first parent + the third part of the second parent.
Mutation operator
Variable Neighborhood Search (VNS) is used in this paper for the mutation structure. The VNS structure applies four Neighborhood Search Structures (NSS). These four structures are used in the framework of VNS and the entire structure can be demonstrated by Figure 5. The pseudo-code of our VNS is as follows.
{for each input particle K=1
While the stopping criterion is met do
New particle=Apply NSS type k (Input particle)
If new particle is better than input particle then K=1
Input particle= new particle; Else K=k+1 If k=5 then K=1 Endif Endif Endwhile }
Fig. 5. Shows the VNS algorithm Strategy in dealing with the constraints
The mutation operator is designed in a way that no infeasible solution can be generated. Just, the crossover operator may lead to infeasible solutions. Since new solutions are generated during the algorithm implementation, a specific procedure has been deployed to check whether the constraints are satisfied by the given solution or not. Hence, if it is necessary, the feasible solutions remain and infeasible solutions can be transformed into feasible ones. The mentioned procedure tries to transform the solution into an acceptable one, whenever one or more constraints are dissatisfied by the obtained solution.
Stopping criterion
The algorithm is terminated when it cannot find a new solution anymore, or in other words the objective function values do not change.
Design of experiments
To investigate the validity and feasibility of the proposed mathematical model, different small-sized problems are solved by the conventional branch-and-bound (B&B) solver in the GAMS software. In order to do that, ten random instances are taken into account. Afterwards, the results are compared with those of the GA to validate the approach. The obtained results of the GA are compared with the exact ones of GAMS, as shown in Table 1. The parameters are set with respect to the following intervals.
Establishment cost of distribution centers by different capacity levels ~ U[650-5500]
Stock level for each distribution center ~ U[0.2, 2.3]
Annual inventory holding cost ~ U[4, 15]
Average demand of each customer ~U[1, 11]
Variance of the customers’ demands ~U[0, 3]
Capacity level of the distribution centers ~U[1, 30]
Processing time of each plant ~U[1, 4]
Service time of distribution centers ~U[1, 5]
Fixed ordering cost in each distribution center ~U[15, 60]
Cost of each demand unit in route r ~U[100, 650]
Available vehicles type v ~U[2, 3]
Table 1. Obtained results of small-sized problems for the GA and GAMS.
Problem GAMS GA Gap (%)
OFV CPU time (sec.) OFV CPU time (sec.)
2×2×3 517670 1.438 517670 0.011 0 2×2×3 697750 1.391 697750 0.013 0 2×2×5 1740100 4.5 1740100 0.002 0 2×2×2 154480 0.468 154480 0.027 0 3×3×3 780490 17.656 780490 0.01 0 3×3×4 2719700 17.985 2719700 0.011 0 3×3×5 3368100 138.593 3368100 0.004 0 3×3×6 3250500 1005.703 3250500 0.017 0 2×2×3 726950 2.406 726950 0.021 0 2×2×2 447130 1.641 447130 0.012 0
The results indicate that the obtained objective function values for the GA and GAMS are the same in small-sized instances. However, the CPU times of the GA are less than GAMS. Given the assumptions and parameters, 30 random instances are considered for medium and large-sized problems. The results are presented in Table 2 in terms of the CPU time and the objective function value (OFV). Each instance is solved for five times by the GA and the average value is illustrated in the tables.
Table 2. Results obtained by the proposed GA.
Medium-sized problems Large-sized problems
Problem No. OFV CPU time (sec.) Problem No. OFV CPU time (sec.)
10×10×15 1542905 3 40×50×50 10929000 10.6825 10×10×20 1700312 2.8 40×50×60 11211000 11.1 10×10×25 2419531 2.825 40×50×70 12748000 12.8 10×10×30 2569362 2.925 40×50×80 12789000 15.275 10×15×15 3149300 2.9 40×50×90 13734000 17.475 10×15×20 3573900 2.9 40×50×100 14007000 20.1 10×15×25 3747400 3.475 50×70×50 16988000 14.35 10×15×30 4001100 3.525 50×70×60 17765400 19.125 10×20×25 4127800 4.725 50×70×70 16997000 22.775 10×20×30 4462900 5.5 50×70×80 16371000 27.575 10×20×40 4683200 4.975 50×70×90 17342000 34.975 10×25×30 5999300 4.95 50×70×100 18756000 34.825 10×25×40 5219400 4.975 50×70×120 15023000 47.625 10×25×50 5670000 5.525 50×70×140 16917000 52.75 10×30×40 6464700 6.05 50×80×90 17600000 36.95 10×30×50 6298800 6.3 50×80×100 17008000 44 10×30×60 6700000 7.275 50×80×120 18432900 56.125 15×15×20 4643900 2.825 50×80×140 17699000 70.3 15×15×25 3800000 3.075 50×80×160 19809000 89.675 15×15×30 4098900 3.2 50×90×100 20112000 52.75 15×20×25 5098900 3.9 50×90×120 22259000 49.975 15×20×30 5210000 3.825 50×90×140 21977000 72.675 15×20×40 5329100 4.225 50×90×160 20033000 92.725 15×25×30 5765400 4.3 50×90×180 21098000 122.3 15×25×40 5032000 5.5 50×100×110 24989000 72.775 15×25×50 5099900 5.575 50×100×120 24396000 69.25 15×30×30 6765900 4.975 50×100×140 24164000 92.2 15×30×40 7098700 5.94 50×100×160 24621000 125.15 15×30×50 7379900 6.4525 50×100×180 26791000 150.1 15×30×60 7100200 7.475 50×100×200 28866000 181.775
In order to show the proper performance of the GA for the given problems, the following assumptions should be taken into account.
Rates of the mutation and crossover operators are assumed to be 0.1 and 0.8, respectively.
Local-iteration is assumed equal to 5.
Population size is assumed to be 100.
Initial population is generated randomly.
The parameters are set with respect to the following intervals.
Etablishment cost of distribution centers by different capacity ~ U[1,40]
Stock level for each distribution center ~ U[0, 3]
Annual inventory holding cost ~ U[1, 40]
Average demand of each customer ~U[1, 100]
Variance of the customers’ demands ~U[1, 4]
Capacity level of the distribution centers ~U[1000, 2500]
Processing time of each plant ~U[1, 40]
Service time of distribution centers ~U[1, 40]
Fixed ordering cost in each distribution center ~U[1, 40]
Cost of each demand unit in route r ~U[1, 100]
Available vehicles type v ~U[1, 10]
Number of possible routes related to distributor j ~U[1, r]
Sensitivity analysis
The effective rates of mutation and crossover and the efficient population size are given below. The rate of the mutation is equal to 0.1, and the value of the crossover rate is considered equal to 0.6, 0.7 and 0.8. The three levels can be seen in Figure 6, so that each level shows the combination of the rate of two operators (Naderi et al., 2009).
a1: rate 0.6 for crossover and 0.1 for mutation. a2: rate 0.7 for crossover and 0.1 for mutation. a3: rate 0.8 for crossover and 0.1 for mutation.
The vertical axis shows the value of a criterion, namely relative percentage deviation (RPD), which is calculated by: 100 min min Alg sol sol sol RPD (16)
where the Algsol is the objective function value for each problem by combining the parameters and Minsol
is
the
minimum objective function value in all the combinations. In fact, each instance is run by each of the three combinations and the RPD criterion is calculated for each one. The results are presented in Figure 6. In this fig-ure, it is obvious that the best crossover rate is 0.8.In addition, the crossover rate is equal to 0.8 and the mutation rates are set to 0.1 and 0.2. Two levels are seen in this figure, so that each one is a combination of the rate of two operators given below.
a1: the rates 0.8 for crossover and 0.1 for mutation. a2: the rates 0.8 for crossover and 0.2 for mutation.
In fact, each problem is carried out by each of two possible combinations and the RPD criterion is calculated for each problem. It is concluded that the best mutation rate is 0.1 as depicted in Figure 7.
a3 a2 a1 3.0 2.5 2.0 1.5 1.0 0.5 0.0 Da ta
analysis for crossover rate
RPD
95% CI for the Mean
Fig. 6. RPD diagram with respect to combinations of the fixed mutation rates and different Crossover rates
a2 a1 3.0 2.5 2.0 1.5 1.0 0.5 Da ta
analysis for mutation rate
RPD
95% CI for the Mean
Fig. 7. RPD diagram with respect to combinations of the fixed Crossover rates and different mutation rates
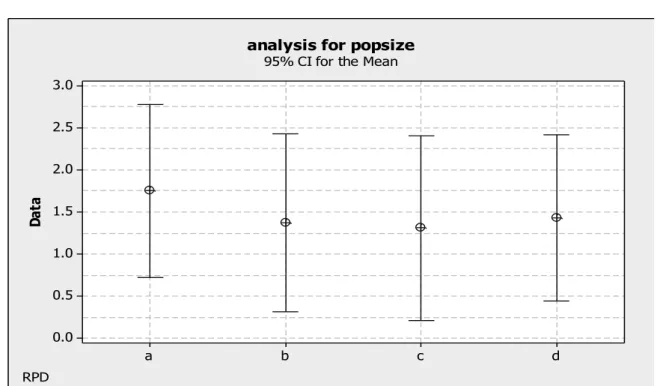
Figure 8 pertains to the population size. Four different sizes (i.e., 30, 50, 100 and 200) are considered as shown below:
a: shows size 30 b: shows size 50 c: shows size 100 d: shows size 200
where the Algsol is the objective function for each level of the population size for each problem, which is obtained by the algorithm and Minsol is the minimum calculated value among all the considered size levels for each problem. As it is observed from Figure 8, the most efficient and reliable population size is 100.
d c b a 3.0 2.5 2.0 1.5 1.0 0.5 0.0 Da ta
analysis for popsize
RPD
95% CI for the Mean
Fig. 8. RPD diagram regarding the population size
Conclusions
In this paper, a new mathematical model for designing the multi-echelon supply chain has been presented by considering the inventory under uncertain demands, risk-pooling, lead time and vehicles routing. This model has been formulated for the first time as a location-inventory-routing problem with a risk-pooling strategy in a multi-echelon supply chain. Feasibility of the developed model was checked by presenting small-sized random instances and solving them by commercial optimization software. Then, the results obtained from the GA were compared to the exact ones of GAMS in small-sized instances in order to validating the GA. The results showed that the CPU times were less for the GA in comparison with those of GAMS. A number of medium and large-sized problems were solved by the proposed GA because of the NP-hardness of the given problems. Some future studies are as follows: considering each parameter as a fuzzy, time windows, multi-period planning and solving the presented model by the use of heuristic or other meta-heuristic algorithms.
References
Ahmadi Javid, A., Azad, N., 2010. Incorporating location, routing and inventory decisions in supply chain net-work design. Transportation Research Part E: Logistics and Transportation Review 46, 582-597.
Bettinelli, A., Ceselli, A., Righini, G., 2011. A branch-and-cut-and-price algorithm for the multi-depot heteroge-neous vehicle routing problem with time windows. Transportation Research - Part C: Emerging Technolo-gies 19, 723-740.
Chang, Y.-H., 2010. Adopting co-evolution and constraint-satisfaction concept on genetic algorithms to solve supply chain network design problems., Expert Systems with Applications 37, 6919-6930.
Goldberge, D.E., Genetic algorithms in search, optimization and machine learning, Addison-Wesley Publishing, 1989. Gupta, A., Maranas, C.D., McDonald, C.M. 2000. Mid-term
Customer demand satisfaction and inventory management. Computers & Chemical Engineering 24, 2613-2621. Kannan, G., Sasikumar, P., Devika, K., 2010. A genetic
al-gorithm approach for solving a closed loop supply chain model: A case of battery recycling. Applied Mathematical Modeling 34, 655-670.
Marinakis, Y., Marinaki, M., 2010. A hybrid genetic-particle swarm optimization algorithm for the vehicle routing problem. Expert Systems with Applications 37, 1446-1455.
Naderi, B., Khalili, M., Tavakkoli-Moghaddam, R., 2009. A hybrid artificial immune algorithm for a realistic vari-ant of job shops to minimize the total completion time. Computers & Industrial Engineering 56, 1494-1501. Paksoy, T., Chang, C.T., 2010. Revised multi-choice goal
programming for multi-period, multi-stage inventory controlled supply chain model with popup stores in Guerrilla marketing. Applied Mathematical Modeling 34, 3586-3598.
Park, S., Lee, T.E., Sung, C.S., 2010. A three-level supply chain network design model with risk-pooling and lead times. Transportation Research - Part E: Logistics and Transportation Review 46, 563-581.
Wang, K.-J., Makond, B., Liu, S.-Y., 2011. Location and allocation decisions in a two-echelon supply chain with stochastic demand – A genetic-algorithm based solu-tion. Expert Systems with Applications 38, 6125-6131. You, F., Grossmann, I.E., 2009. Optimal design of
large-scale supply chain with multi-echelon inventory and risk pooling under demand uncertainty. Computer Aid-ed Chemical Engineering 26, 991-996.
Yun, Y., Moon, C., Kim, D., 2009. Hybrid genetic algo-rithm with adaptive local search scheme for solving multistage-based supply chain problems. Computers & Industrial Engineering 56, 821-838.
Zegordi, S.H., Kamal Abadi, I.N., Beheshti Nia, M.A., 2010. A novel genetic algorithm for solving production and transportation scheduling in a two-stage supply chain. Computers & Industrial Engineering 58, 373-381.