On the stress–force–fabric relationship for granular materials
Full text
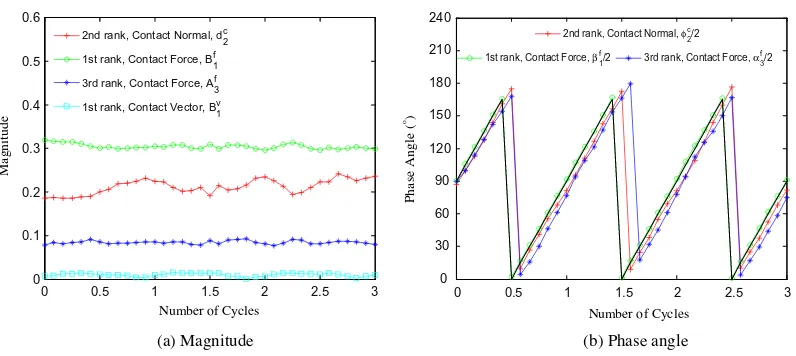
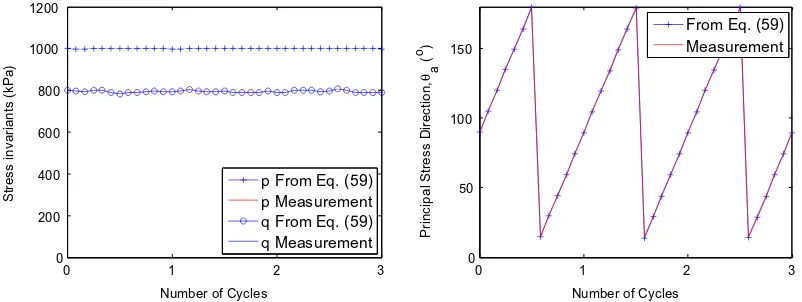
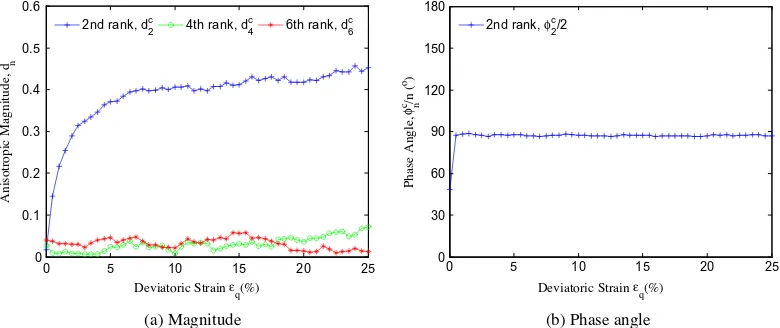
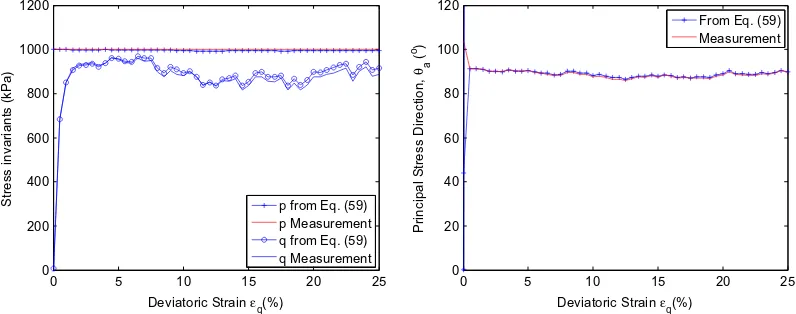
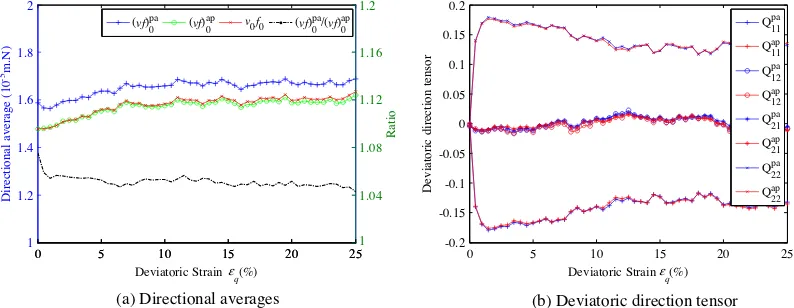
Figure

Related documents
While the thermal denatu- ration curves of reduced barstar and barstar(ESOA) obtained by far and near UV CD are virtually identical, the tertiary structure in both
At temperatures above 572°F / 300°C, this product can decompose to form hydrogen fluoride (HF), but HF will only accumulate with continuous exposure to excessive heat in a
Sales location, product type, number of advertising methods used, high-speed Internet connection, land tenure arrangement, and gross farm sales is found to be significantly related
Newby indicated that he had no problem with the Department’s proposed language change.. O’Malley indicated that the language reflects the Department’s policy for a number
Proposition 103 specifically refers to only several parts of the administrative rate review process: Section 1861.05, subdivision (b) provides that an insurer which desires to
The topic of this particular briefing is Attention Deficit/Hyperactivity Disorder (ADHD), and the related disorder or sub-type, Hyperkinetic Disorder (HKD), although the
“The Significance of SAAPM Is that it’s celebrated throughout the entire Department of Defense to bring awareness to the prevention of sexual assault in the hopes to eliminate it
In Queensland, the Queensland Transcultural Mental Health Centre (QTMHC) is a state-wide service working in partnership with the national body and other mainstream mental