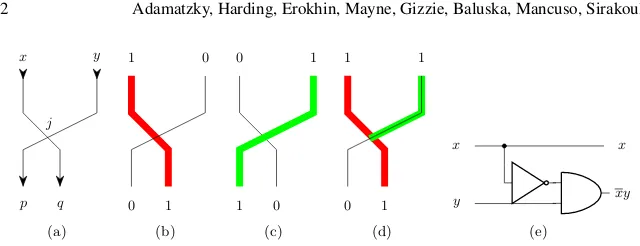
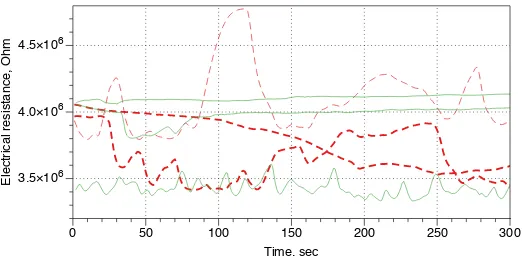
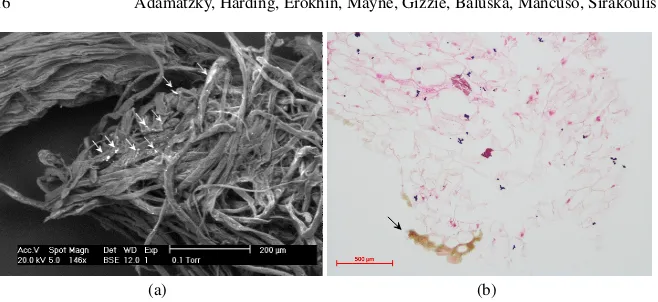
Computers from plants
32
0
0
Full text
Figure
![Fig. 1 Plant roots select a path towards attractant. Reprinted from [108]. (a) Control experiment.The maize roots are growing Y-maze with 1 ml of distilled water in both slanted channels](https://thumb-us.123doks.com/thumbv2/123dok_us/572218.556754/5.612.166.436.293.437/attractant-reprinted-control-experiment-growing-distilled-slanted-channels.webp)


+7
Related documents
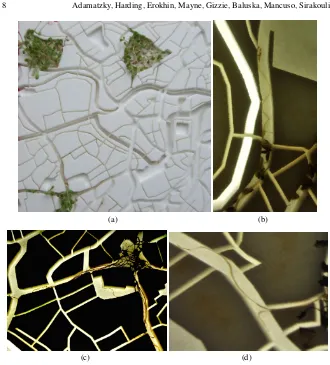
![Fig. 6 Approximation of Voronoi diagram with growing and branching roots. See details of com-puter model in [10]](https://thumb-us.123doks.com/thumbv2/123dok_us/572218.556754/9.612.142.464.89.337/approximation-voronoi-diagram-growing-branching-roots-details-puter.webp)
![Fig. 7 Illustration on how a polygon can be subdivided by plant roots. The original model refersto liquid crystal fingers [10] but mechanisms of interaction could be the same](https://thumb-us.123doks.com/thumbv2/123dok_us/572218.556754/11.612.139.465.78.189/illustration-polygon-subdivided-original-refersto-ngers-mechanisms-interaction.webp)