Profits, efficiency and Irish banks
Full text
Figure

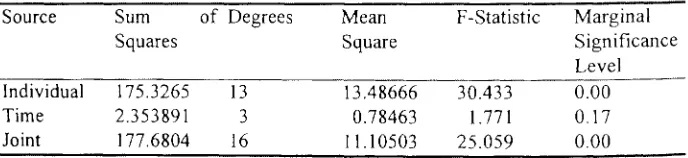
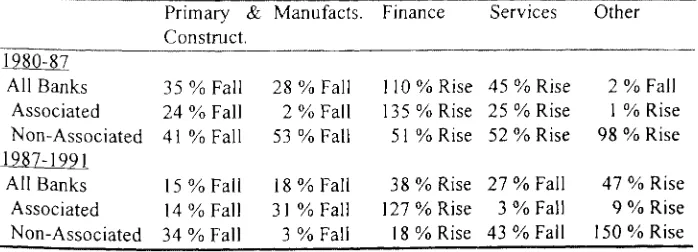
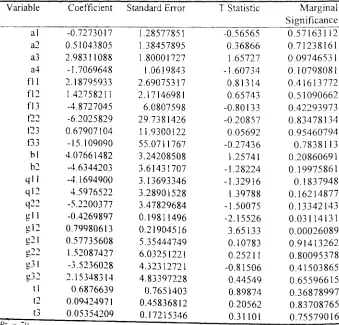
Related documents
assumptions, formulas, etc. so that a reviewer could replicate the calculations based on the data provided. All assumptions and estimates must be clearly identified. As noted in
Christ before Pilate at the trial of Jesus revealed one of his last claims. Jesus and his word are ultimate truth. The Pontius Pilate and Jesus exchange set the two positions
For establishments that reported or imputed occupational employment totals but did not report an employment distribution across the wage intervals, a variation of mean imputation
I argue that positive global coverage of Jamaica’s outstanding brand achievements in sports, music and as a premier tourism destination, is being negated by its rival brands –
Minors who do not have a valid driver’s license which allows them to operate a motorized vehicle in the state in which they reside will not be permitted to operate a motorized
The result of ordinal logit model revealed that high school type, family income, and whether students live in dorm, mother education and university entrance score positively
(2010) Effect of Fly Ash Content on Friction and Dry Sliding Wear Behaviour of Glass Fibre Reinforced Polymer Composites - A Taguchi Approach. P HKTRSR and
In this way, the different categories for in-situ classification are first detailed, followed by the corresponding characterization and filtering of events after adding the