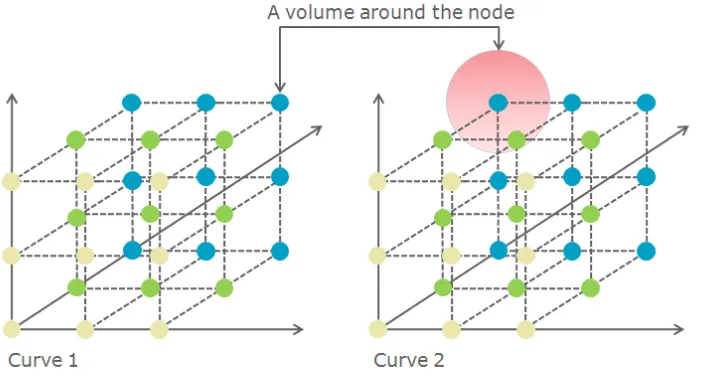
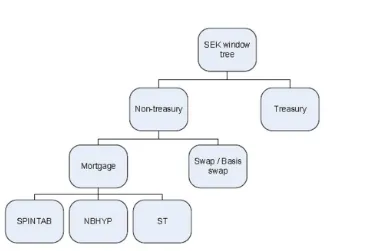
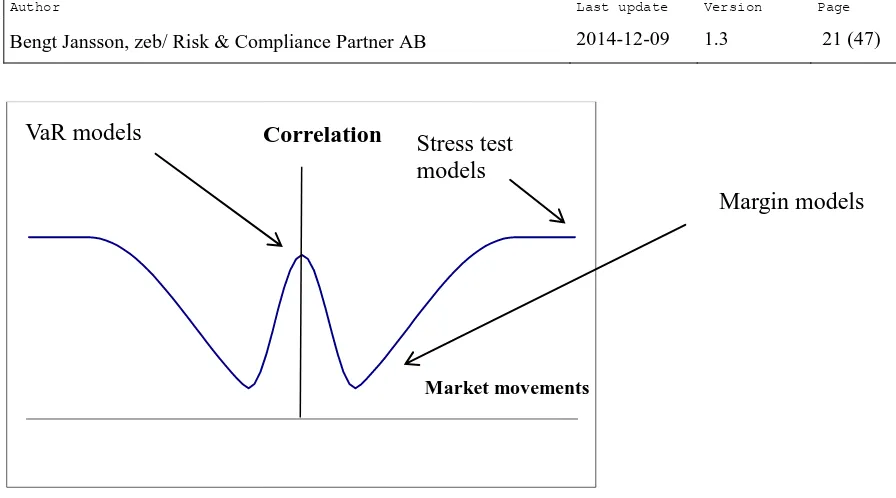
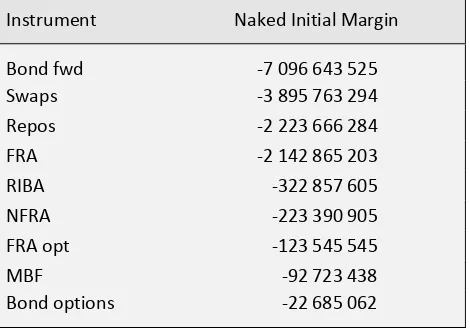
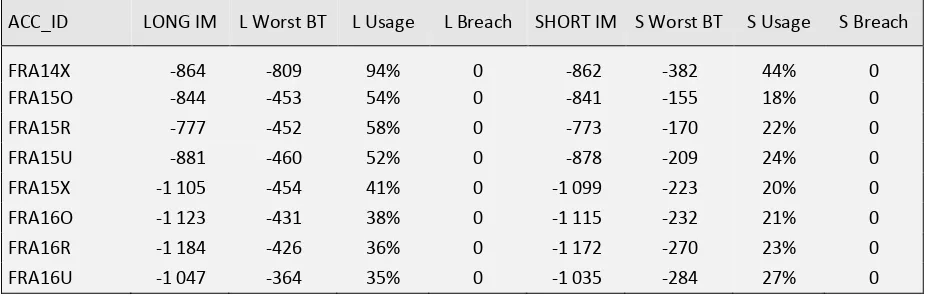
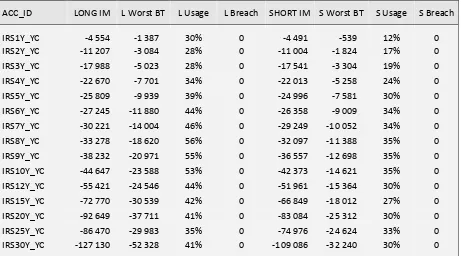
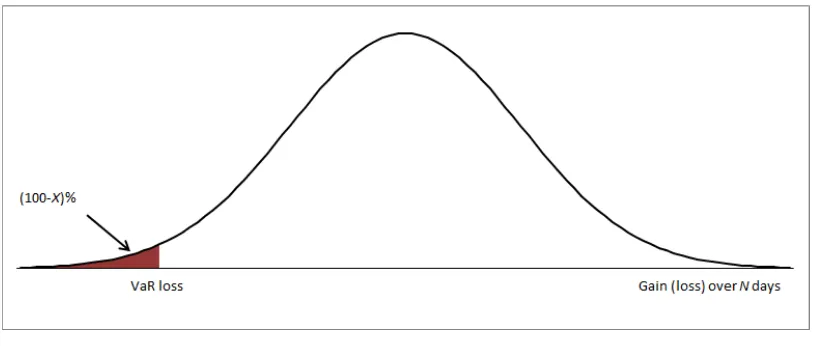
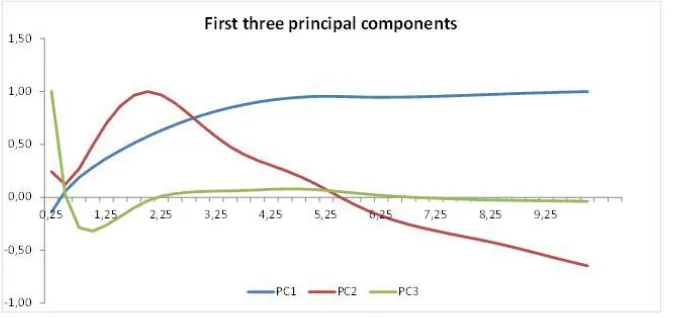
Validation of CFM A validation of the Margin Model CFM for interest rate products used by Nasdaq OMX
Full text
Figure
Related documents
For interval-valued intu- itionistic fuzzy multicriteria group decision-making problem with incomplete information on the weights of criteria, an entropy weight model is established
In this present study, antidepressant activity and antinociceptive effects of escitalopram (ESC, 40 mg/kg) have been studied in forced swim test, tail suspension test, hot plate
Satcom and IT Engineering and Management Consulting, Program & Project Management, Technical Support Services, Satcom and IT network design, installation and maintenance
EMT: Epithelial-to-mesenchymal; EndMT: Endothelial-to-mesenchymal transition; HFD: High-fat diet; HUVECs: Human umbilical vein endothelial cell line; LDL-C: Low-density
This gives us the possibility to observe the features selected by different feature selection approaches and to assess classification performance of different classification
According to that idea, this paper proposes a model for estimating VoIP quality provided by G.729, a common codec used over WAN, that has been created from subjective Mean
The observed difference compared with integrated buoyant jet models can be attributed to four possible effects: (i) entrainment of turbulent kinetic energy from the ambient