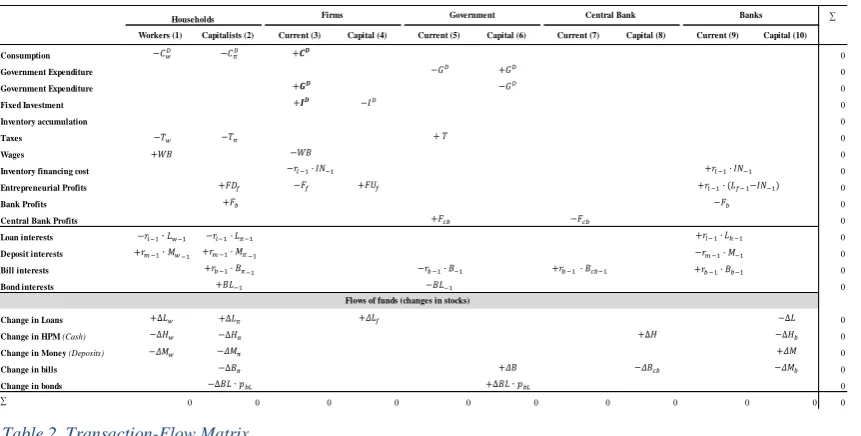
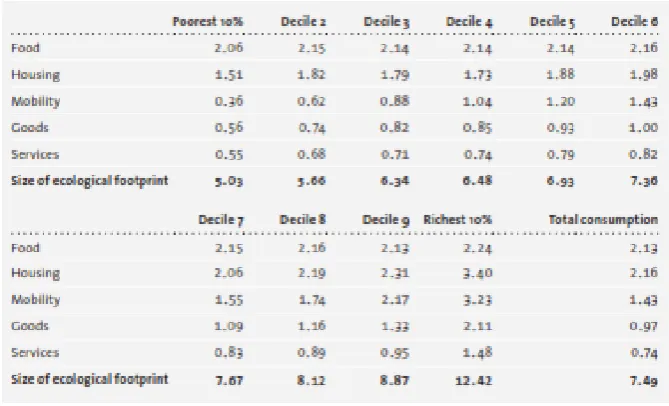
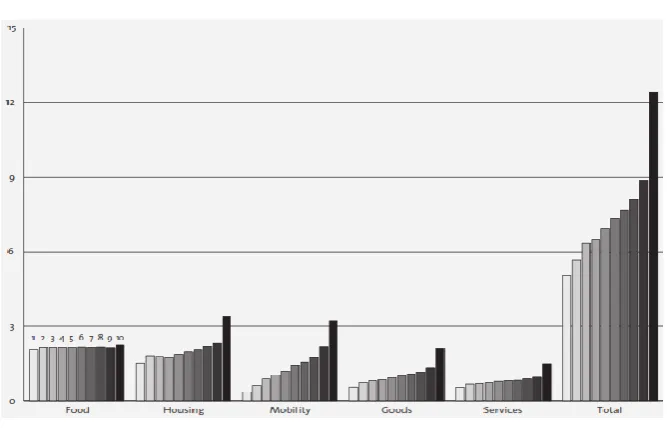
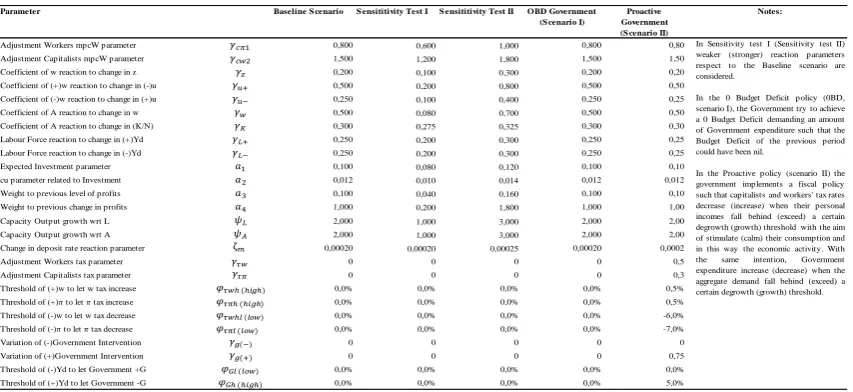
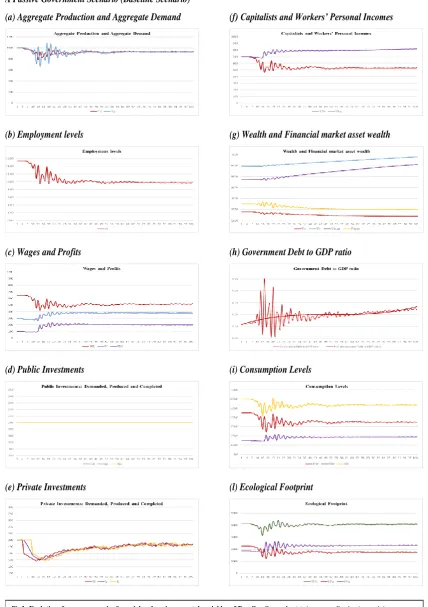
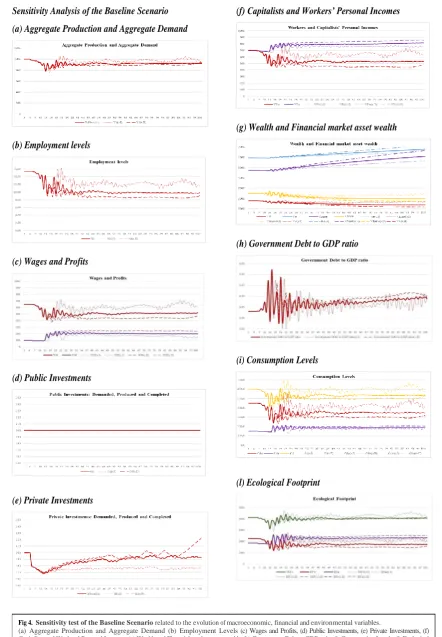
The State Again
Full text
Figure
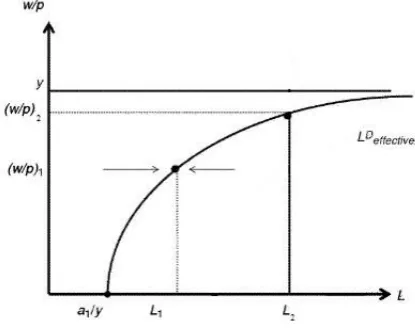
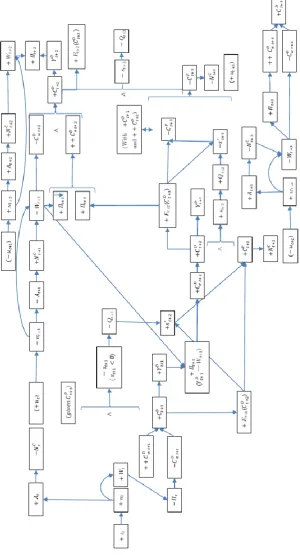

Outline
Related documents
Second, managers can develop chatbot service monitor programs by using the incident sorting process established by this study (Figure 2), which could be a useful tool to
Institution covering scientific contents HEALTH SURVEILLANCE Hospital Infections Committee (CIO) Role of CIO Organization Defects Structure Problems Antibiotics Resistance Problems
This qualitative phenomenological study sampled fourteen experienced educators in the Central Virginia region with similar educational qualifications, including licensure to be
The key players covered in this study GE Microsoft Stratasys Oculus ABB Mitsubishi Electric Intel HPE Siemens Cisco Systems Samsung Electronics Rockwell Automation Denso
The map depicts age-adjusted and spatially smoothed county-specific heart failure (HF) hospitalization rates per 1,000 among fee-for-service Medicare beneficiaries, age 65 years
The encryption operation for PBES2 consists of the following steps, which encrypt a message M under a password P to produce a ciphertext C, applying a
Scope definition and many of the practices defined in the PMBOK knowledge area of Project Time Management are done as part of iteration planning, where features are elaborated,
This paper articulates how the first phase of a design research approach was applied to explore possible solutions for designing and implementing effective online higher