Compact quad band BPF design with fractal stepped impedance ring resonator
Full text
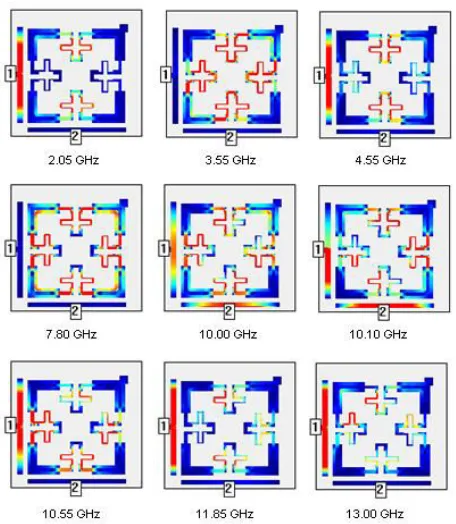
Figure
Related documents
+HQFHWKHWUHQGWKDWFDQEHVHHQKHUHLVWKDWDVIUHTXHQF\LQFUHDVHVWKHGLIIHUHQFHEHWZHHQ WKHHQHUJ\FRQVXPSWLRQRIDQRGHWKDWUXQV67,EDVHGWKUHDGVDQGRQHWKDWUXQV,65EDVHG WKUHDGV UHGXFHV 7KLV LV GXH WR
With the systematic security test plan, Smith and Williams [35] found 17 input validation vulnerabilities. Of these 17 vulnerabilities, we were able to find six of these with
Table S1: statistical models for differential expression analysis; Figure S1: se- quence read integrity and mapping results; Figure S2: SOM clusters of differentially expressed
Apparently the dominant eye-color gene is located exactly a t the point of breakage of one of the chromosomes, since the mutation never separates from the
Total 23 feature of texture like contrast, homogeneity, energy, correlation of GLCM in four orientations and seven set of Moment Invariant have been calculated
Computer simulation and integral equation calculations predict an isotropic–nematic transition at low temperatures in zero field and an in-plane transition at somewhat
It may accord- ingly be concluded that none of the 35 forked (not-fused) offspring repre- sented equal crossing over between the halves of the two double-type bar