GENETIC PROGRAMMING FOR
OBJECT DETECTION
MS. V. A. PATIL,
ADCET, Ashta viddulata@gmail.com
PROF. S. R. JAGTAP,
RIT, Sakharale
satyawan.jagtap@ritindia.edu
Abstract
In this paper an approach to improve efficiency of Object Detection problem using Genetic Programming in terms of reducing false positives and improving processing speed is presented. We developed a new fitness function taking into consideration the mean squared error (MSE) between obtained output and desired output for training purposes based on existing function which uses linear combination of Detection Rate and False Alarm Rate,. By considering a fixed step size for the sweeping window, we showed that the false alarm rate and time taken to converge was reduced drastically, at the cost of higher tolerance. By taking three data sets of different coins against different backgrounds, we experimented with this approach on data sets. We showed the effect of changing the window size and step size on efficiency. We showed that using genetic operators like mutation to a larger extent proves more favorable than the crossover operator for the purpose of selecting population of programs for subsequent generations. This approach has proved to work sufficiently well with different kinds of objects against different backgrounds.
Index Terms—Genetic Programming, Fitness function, Object Detection, Detection Rate, False Alarm Rate
INTRODUCTION
OBJECT detection is used in a very wide range of applications, such as detecting faces from video images, finding tumors in a database of x-ray images, and detecting cyclones in a database of satellite images [1], [2], [3], [4]. In many cases, highly trained experts are able to perform the detection task well, but there is either a shortage of such experts, or the cost of people is too high. In such cases computer based object detection systems are preferable. However, creating such automated systems that have sufficient accuracy and reliability is very difficult.
Genetic programming (GP) is a relatively recent and fast developing approach to automatic programming. The GP paradigm first introduced by Koza [4] is a domain independent method. In GP, solutions to a problem are represented as computer programs. Darwinian principles of natural selection and recombination are used to evolve a population of programs to get effective solution to specific problems. As the computer programs represented in GP are flexible and more expressive, GP is the exiting method to solve problems. Finding a good fitness function for a particular object detection problem is an important but difficult task in developing a GP system. Various fitness functions have been devised for object detection, with varying success.
The term object detection here refers to the detection of small objects in large images. This includes both object classification and object localization. Object classification refers to the task of discriminating between images of different kinds of objects, where each image contains only one of the objects of interest. Object localization refers to the task of identifying the positions of all objects of interest in a large image. The object detection problem is similar to the commonly used terms automatic target recognition and automatic object recognition. Object detection performance is usually measured by detection rate and false alarm rate. The detection rate (DR) refers to the number of small objects correctly reported by a detection system as a percentage of the total number of actual objects in the image(s). The false alarm rate (FAR),also called false alarms per object , refers to the number of non-objects incorrectly reported as objects by a detection system as a percentage of the total number of actual objects in the image(s). Note that the detection rate is between 0 and 100%, while the false alarm rate may be greater than 100% for difficult object detection problems.
OUR APPROACH
We have proposed a training method wherein we pass a sliding window of fixed size over the image containing objects which are to be localized. During the object localization process, a genetic program might consider many pixel positions in an image as object centers and we call each object centre localized in an image by a genetic program a localization. The size of the window and the step size are fixed. By allowing a fixed step size, we reduce the number of false alarms obtained. As we reduce the step size, chances of obtaining the correct localizations closer to the actual object center increases. However the smaller the step size, the more false alarms we obtain. As the window moves along, it collects the required terminals for the terminal set specified in the subsequent section. An initial random population is created. The population is a set of randomly generated computer programs. Each generated program is evaluated for fitness and the fittest programs are selected and reinserted into the population. This is the reproduction operator. Pairs of programs are used to create new programs by means of crossover operator. The Mutation operates only on a single selected program and introduces new genetic code in the new generation. The procedure is repeated till a specified number of iterations or till termination criteria is satisfied. In the test procedure, the best evolved genetic program obtained in the learning process is then applied to the entire images in the test set to measure object detection performance.
A. TERMINAL SET
The terminal set is the array of features that we supply to the generated programs. For object detection problems, terminals generally correspond to image features. In this approach, to avoid the problem of hand-crafting of feature extraction programs, the features are extracted by calculating the mean and standard deviation of pixel values within the sweeping window. This set of features has the advantages of being rotationally invariant. The terminals i.e Mean and Standard deviation are as follows:
1
1
Where
N = the total number of pixels in the window which are being considered, Xi = the i th pixel and
= the mean of pixels for i=1 to N
= the standard deviation of the pixels under the window.
B. FUNCTION SET
The function set contains the four standard arithmetic and a conditional operation: FuncSet = {+, −, *, /, if}. The +, − and * operators are usual addition, subtraction and multiplication, while / represents “protected” division. The if function returns its second argument if the first argument is positive or returns its third argument otherwise.
C. DATA SETS
(a) (b) (c) Fig.1. coin data set (a)easy (b) medium (c)hard
D. FITNESS FUNCTION
Our aim is that the program evolved should identify the singular and precise location of the “object”. This can be paraphrased as identification of the center of the “object”. However, in the usual case, these evolved genetic programs will also detect some “objects” not only when the sweeping window is within a few pixels of the centre of the target objects, but also when the sweeping window is centered over a number of cluttered pieces of background. Clearly, these “objects” are not those we expected but false alarms. We have focused on elimination of maximum number of false alarms by including a weight factor which is directly proportional to the distance of the detected object from the actual object. We have considered some of the previous work on fitness function and built up from there.
The function used is:
fitness A* MSE +B * (1- DR) +C *FAR
where DR and FAR are detection rate (the number of small objects correctly reported by a detection system as a percentage of the total number of actual objects in the images), false alarm rate (also called false alarms per object, the number of non-objects incorrectly reported as objects by a detection system as a percentage of the total number of actual objects in the images).
DR = ∑ ∑ 100
FAR = ∑ ∑ ∑ 100
Ntrue is the number of true objects correctly reported Nknown is the number of actual (or known) objects Nreported is the number of objects reported
MSE the mean square error between each localization and the potential true object. MSE is calculated as
MSE =∑ min ∑ Ci Xj
Here Ci is the set of known coin locations from i=1 to m and Xj is the set of calculated coin locations from j=1 to N.
The values of A, B and C are assigned according to the relative importance of the factors, MSE, DR and FAR respectively.
E. PARAMETERS AND TERMINATION CRITERIA
The parameter values used in this approach are shown in table 1. In this approach, the learning/evolutionary process is terminated when one of the following conditions is met:
1) The detection problem has been solved on the training set, that is, all objects in each class of interest in the training set have been correctly detected with no false alarms. In this case, the fitness of the best individual program is zero.
Table 1 PARAMETER FOR GP TRAINING
Parameter Kinds
Parameter Names
Search
parameters
Population size
100
Maximum generations
20
Genetic Parameters
Reproduction rate
50%
Cross-rate
20%
Mutation-rate
30%
Fitness Parameters
A
10
B
10
C
20
IV. RESULTS
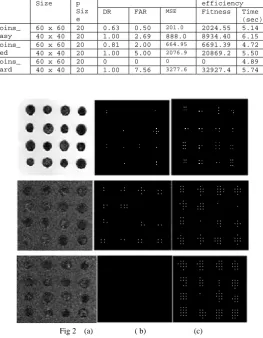
Keeping in consideration the aim of the project, it has been inferred that the mutation rate must be kept higher than the crossover rate. The basic concept of crossover is to take part of two existing parents programs to create a fitter child program. However, the diversity is restricted since by taking already existing characteristics, a new characteristic which may make the program fitter will be suppressed. After experimentation, we concerted that by keeping the mutation rate higher than crossover, this particular problem provides relatively better convergence in terms of time. It has been decided, after experimentation that the weight for the detection rate must be highest, followed by MSE and then false alarm rate. These have found to produce optimum results. The parameters used in this method are displayed in Table1.By using the fixed step size method, and increasing the window size we are able to produce results with far lesser False Alarms as compared to previous methods. Not just are false alarms reduced, but time taken to achieve results is reduced. But the size of the window is restricted to the radius of the object to be detected which is observed in Table 2
Table 2 RESULTS OF THE GP SYSTEMS
Image Window Size
Ste p Siz e
Test Accuracy Training
efficiency
DR FAR MSE Fitness Time
(sec) coins_
easy
60 x 60 20 0.63 0.50 201.0 2024.55 5.14
40 x 40 20 1.00 2.69 888.0 8934.40 6.15
coins_ med
60 x 60 20 0.81 2.00 664.95 6691.39 4.72
40 x 40 20 1.00 5.00 2076.9 20869.2 5.50
coins_ hard
60 x 60 20 0 0 0 0 4.89
40 x 40 20 1.00 7.56 3277.6 32927.4 5.74
Fig.2. (a) coin images with different background (b) shows coins detected locations for window size 60x60 (c) shows coin detected locations from image for window size 40x40
Table 3 Results for step size=15
Image Window Size
Step Size
Test Accuracy Training
efficiency
DR FAR MSE Fitness Time
(sec) coins_
easy
60 x 60
15 0.69 1.06 639.6 6420.8 6.24
Fig.3 Results for step size=15
If step size is reduced number of detected coin increases but at the same time false alarm increases which are specified in Table 3.
From the above results, it can be inferred that our method has proved superior in terms of reducing false positives and processing time. If the window size and step size was to be decreased by half, it would result in higher detection and hence higher accuracy but with increase in processing time and false alarm rate.
V. CONCLUSIONS
The goal of our paper was to show the effect of addition the mean squared error factor to the already existing fitness function to prove better convergence. This was combined with the goal of using fixed step size instead of moving the sweeping window to each consecutive location for purpose of acquiring the terminal set. These two approaches were combined with increasing the mutation operator relative to the crossover operator for the reason that with the crossover operator, the diversity is of the programs generated is restricted since by taking already existing characteristics, a new characteristic which may make the program fitter will be suppressed. From the results obtained by the experimentation of the above approaches, we inferred that reduced step size caused the processing time to be reduced by compared to the previous method. By keeping the mutation rate higher than crossover, this particular problem provides relatively better convergence in terms of time. The MSE calculated works towards reducing the False alarm rate. However this approach has a limitation of increased tolerance due to the step size used. As the step size increases, the error between the actual localization and desired localization increases. This is the problem which needs to be improved upon in future work
.
References
[1] U. Bhowan, “A domain independent approach to multi-class object detection using genetic programming,” BSc Honours research thesis,School of Mathematical and Computing Sciences, Victoria University of Wellington, 2003.
[2] Walter Alden Tackett, “Genetic programming for feature discovery and image discrimination”. In Stephanie Forrest, editor, Proceedings of the 5th International Conference on Genetic Algorithms, ICGA-93, pages 303– 309, University of Illinois at Urbana-Champaign, 17–21 July 1993.
Morgan Kaufmann.
[3] Jamie R, Sherrah, Robert E. Bogner, and Abdesselam Bouzerdoum, “The evolutionary pre-processor: Automatic feature extraction for supervised classification using genetic programming”. In John R. Koza, Kalyanmoy Deb, Marco Dorigo, David B. Fogel, Max Garzon, Hitoshi Iba, and Rick L. Riolo, editors, Genetic Programming 1997: Proceedings of the Second Annual Conference, pages 304–312, Stanford University, CA,USA, 13–16 July 1997. Morgan Kaufmann.
[5] J. R. Koza, “Genetic programming: on the programming of computers by means of natural selection”. London, England: Cambridge, Mass.: MITPress, 1992.
[6] Mengjie Zhang, Malcolm Lett, “Genetic Programming for Object Detection: Improving Fitness Functions and Optimising Training Data”
[7] Mengjie Zhang, Member, IEEE, Xiaoying Gao, and Weijun Lou, “A New Crossover Operator in Genetic Programming for Object Classification”
[8] W. Banzhaf, P. Nordin, R. E. Keller, and F. D. Francone, Genetic Programming: An Introduction on the Automatic Evolution of computer programs and its Applications. San Francisco, Calif. : Morgan Kaufmann Publishers; Heidelburg : Dpunkt-verlag, 1998, subject: Genetic programming (Computer science); ISBN: 1-55860-510-X.
[9] M. Zhang, V. Ciesielski, and P. Andreae, “A domain independent window approach to multiclass object detection using genetic programming,”EURASIP Journal on Signal Processing, Special Issue on Genetic and Evolutionary Computation for Signal
[10] S. F. Smith, “A learning system based on genetic adaptive algorithms,” Ph.D. dissertation, Univ. Pittsburgh, Pittsburgh, PA, 1980. [11] N. L. Cramer, “A representation for the adaptive generation of simple sequential programs,” in Proc. Int. Conf. Genetic Algorithms
and Appl. ,J. J. Grefenstette, Ed., Jul. 24–26, 1985, pp. 183–187.
[12] Andrew Innes, Vic Ciesielski, John Mamutil, Sabu John, “Reducing False Alarms using Genetic Programming in Object Detection” In Proceedings of the 2004 International Conference on Artificial Intelligence (ICAI’04) , H. Arabnia (Editor), pages 569-574, Las Vegas, June 2004, CSREA Press.
[13] J. F. Winkeler, B. S. Manjunath, “Genetic programming for object detection,” in Proc. 2ndAnnu. Conf. Genetic Program. J. R. Koza, K.Deb, M. Dorigo, D. B. Fogel, M. Garzon, H. Iba, and R. L. Riolo, Eds., Jul. 13–16, 1997, pp. 330–335.