Bicyclic graphs with maximum sum of the two largest Laplacian eigenvalues

R E S E A R C H

Open Access

Bicyclic graphs with maximum sum of the

two largest Laplacian eigenvalues

Yirong Zheng

_{, An Chang}

_{, Jianxi Li}

_{and Sa Rula}

*_{Correspondence:}

yrzheng@xmut.edu.cn 1_{School of Applied Mathematics,} Xiamen University of Technology, Xiamen, Fujian, P.R. China Full list of author information is available at the end of the article

Abstract

LetGbe a simple connected graph andS2(G) be the sum of the two largest Laplacian eigenvalues ofG. In this paper, we determine the bicyclic graph with maximumS2(G) among all bicyclic graphs of ordern, which confirms the conjecture of Guanet al. (J. Inequal. Appl. 2014:242, 2014) for the case of bicyclic graphs.

MSC: 05C50; 15A48

Keywords: Laplacian eigenvalue; largest eigenvalue; sum of eigenvalue; bicyclic graph

1 Introduction

LetG= (V(G),E(G)) be a simple connected graph with vertex setV(G) ={v,v, . . . ,vn}. The numbers of its vertices and edges are denoted byn(G) andm(G) (ornandmfor short). For a vertexv∈V(G), letN(v) be the set of all neighbors ofvinG. The degree of v, denoted byd(v), is the cardinality of|N(v)|, that is,d(v) =|N(v)|. A vertex with degree one is called pendant vertex. Particularly, denote by(G) (orfor short) the maximum degree ofG. The matrixL(G) =D(G) –A(G) is calledLaplacianmatrix ofG, whereA(G) is the adjacency matrix ofGandD(G) =diag(d(v),d(v), . . . ,d(vn)) is the diagonal matrix of vertex degrees ofG. We use the notationInfor the identity matrix of ordernand de-note byφ(G,x) =det(xIn–L(G)) theLaplaciancharacteristic polynomial ofG. It is well known thatL(G) is positive semidefinite and so its eigenvalue are nonnegative real num-ber. The eigenvalues ofL(G) are called theLaplacianeigenvalues ofGand are denoted by μ(G)≥μ(G)≥ · · · ≥μn(G) (orμ≥μ≥ · · · ≥μnfor short), which are always enumer-ated in non-increasing order and repeenumer-ated according to their multiplicity. It is well known thati=n_i=μi= m(G). Note that each row sum ofL(G) is  and, therefore,μn(G) = . Fiedler [] showed that the second smallest eigenvalueμn–(G) ofL(G) is  if and only ifGis disconnected. Thus the second smallest eigenvalue ofL(G) is popularly known as the algebraic connectivity ofG. The largest eigenvalueμ(G) ofL(G) is usually called the Laplacianspectral radius of the graphG. The investigation of Laplacian spectra of graphs is an interesting topic on which much literature focused in the last two decades (see [–]).

LetSk(G) =

i=k

i=μi(G) be the sum of theklargestLaplacianeigenvalues ofG. Hamers in [] mentions that Brouwer conjectured thatSk(G)≤m(G) +

_k+



fork= , , . . . ,n. This conjecture is interesting and still open. Up to now, little progress on it has been made (see [, –]). Whenk= , Haemerset al.[] proved the conjecture by showingS(G)≤

Figure 1 Gn,nandGn+1,n.

m(G) +  for any graphG. Especially whenGis a tree, Fritscheret al.[] improve this bound by showingS(T)≤m(T) +  –_n(T) , which indicates that Haemers’ bound is always not attainable for trees. Therefore, it is interesting to determine which tree has maximum value ofS(T) among all trees of ordern. LetSka,b be the tree of ordernobtained from two starsSa+,Sb+by joining a path of lengthkbetween their central vertices. Guanet al. [] proved thatS(T)≤S(Tn–

 ,n–

) for any tree of ordern≥ and the equality holds if and only ifT∼=Tn–

 ,n–

. Note thatμ(G)≤n(G) for any graphGof ordern. When n(G) <m(G) + , it follows thatS(G)≤n(G) <m(G) + , which means that Haemers’ bound is not attainable. When n(G)≥m(G) + , Guanet al.[] showed thatS(Gm,n) = m(Gm,n) + , whereGm,nis a graph withnvertices andmedges which hasm–n+  triangles with a common edge and n–m–  pendant edges incident with one end vertex of the common edge (illustrated in Figure  areGn,nandGn+,n). This indicates that Haemers’ bound is always sharp for connected graphs (n≤m≤n– ). The following conjecture on the uniqueness of the extremal graph is also presented in [].

Conjecture .([]) Among all connected graphs with n vertices and m edges(n≤m≤ n– ),Gm,nis the unique graph with maximal value of S(G),that is,S(Gm,n) =m(Gm,n) + .

Zhenget al.[] determined the uicyclic graph with maximumS(G) among all uicyclic graphs of ordern, which confirms Conjecture . form=n.

Theorem .([]) For any unicyclic graph G of order n,S(G)≤m(G) + with equality if and only if G∼=Gn,n.

In this paper, we prove that Conjecture . holds form=n+ . The main result is as follows.

Theorem . For any bicyclic graph G of order n,S(G)≤m(G) + with equality if and only if G∼=Gn+,n.

In Section  of this paper, we give some well known lemmas which are useful in the proof of Theorem .. In Section , we will give the proof of Theorem ..

2 Preliminaries

We first present some well-known results onμ(G).

Lemma .([]) Let G be a connected graph of order n,di=d(vi)and mi=

vj∈N(vi)dj/di.

Then

μ(G)≤max

di+mi|vi∈V(G)

.

Lemma .([]) Let G be a connected graph with n≥vertices and m edges.Then

μ(G) <max

(G),m–n–  

+ .

LetMbe a real symmetric matrix of ordern. Then all eigenvalues ofMare real and can be denoted byλ(M)≥λ(M)≥ · · · ≥λn(M) in non-increasing order. The following result in matrix theory plays a key role in our proofs.

Lemma .([]) Let A and B be two real symmetric matrices of order n.Then,for any ≤k≤n,

k

i=

λi(A+B)≤ k

i= λi(A) +

k

i= λi(B).

The next lemma follows from Lemma . immediately.

Lemma . Suppose G, . . . ,Grare edge disjoint graphs.Then,for any k,

Sk(G∪ · · · ∪Gr)≤ r

i= Sk(Gi).

The following lemma can be found in [] and is known as the interlacing theorem of Laplacian eigenvalues.

Lemma .([]) Let G be a graph of order n and Gbe the graph obtained from G by deleting an edge of G.Then the Laplacian eigenvalues of G and Ginterlace,that is,

μ(G)≥μ

G≥μ(G)≥ · · · ≥μn–

G≥μn(G)≥μn

G= .

Lemma .([]) Let A be a real symmetric matrix of order n with eigenvaluesλ≥λ≥

· · · ≥λnand B be a principal submatrix of A of order m with eigenvaluesλ≥λ≥ · · · ≥ λ_m.Then the eigenvalues of B interlace the eigenvalues of A,that is,λi≥λi≥λn–m+i,for i= , . . . ,m.Specially,for v∈V(G),let Lv(G)be the principal submatrix of L(G)formed by deleting the row and column corresponding to vertex v.Then the eigenvalues of Lv(G) interlace the eigenvalues of L(G).

Figure 2 GraphsGandG.

Lemma . Let v be a pendant vertex of graph G with n vertices and G be the graph obtained from G by adding a new vertex vwhich has a unique neighbor u,where u is the neighbor of v. (See Figure.)Then

mG() =mG() + .

Proof LetL(G) andL(G) be the Laplacian matrix ofGandG, respectively. It is not diffi-cult to check thatr(In–L(G)) =r(In+–L(G)). Thus the result follows from the facts that mG() =n–r(In–L(G)) andmG() = (n+ ) –r(In+–L(G)).

LetPnandCnbe the path and cycle of ordern, respectively. A connected graph with nvertices andn+  edges is called a bicyclic graph. LetBnbe the set of bicyclic graphs of ordern. There are two basic bicyclic graphs:∞-graph andθ-graph. More concisely, an∞-graph, denoted by∞(p,q,l)-graph, is obtained from two vertex-disjoint cyclesCp andCqby connecting one vertex of Cp and one vertex ofCq with a pathPl+ of length l, whereq≥p≥ andl≥ (in the case ofl= , we identify the above two vertices). Aθ-graph, denoted byθ(p,q,l), is a union of three internally disjoint pathsPp,Pq,Plof lengthp– ,q– ,l– , respectively with common end vertices, wherel≥q≥p≥ and at most one of them is . Observe that any bicyclic graphGis obtained from a basic bicyclic graph∞(p,q,l) orθ(p,q,l) by attaching trees to some of its vertices. For any bicyclic graph G, we call its basic bicyclic graph ∞(p,q,l) or θ(p,q,l) the kernel ofG. For a vertexv of the kernel of G, if there is a treeTv attached to it, we denote bye(v) the maximum distance betweenvand any vertex ofTv(that is,e(v) =max{d(u,v)|u∈V(Tv)}); if there is no tree attached to it, we definee(v) = . LetB_n∞(p,q,l) and Bθ

n(p,q,l) be the sets of bicyclic graphs of ordernwith∞(p,q,l) andθ(p,q,l) as their kernel, respectively. Clearly,

Bn=B∞n(p,q,l)∪Bnθ(p,q,l). LetSbe a multiset of some nonnegative integers, denote by

Sthe number of nonzero elements inS, that is,S=|{a∈S|a≥}|, where elements are counted according to their multiplicity.

Lemma . Let G be the union of some disjoint graphs G,G, . . . ,Gr, where Gi (i ∈

{, . . . ,r})is a tree or an unicyclic graph of order niwhich is not isomorphic to Gni,ni(Gn,nis

the unicyclic graph shown in Figure).Then S(G) <m(G) + .

Lemma . Let G be a simple graph with at leastvertex-disjoint P(orvertex-disjoint P)such that G– P=

Gi(or G– P=

Gi),where Giis a tree or an unicyclic graph of order niwhich is not isomorphic to Gni,ni(Gn,nis the unicyclic graph shown in Figure).

Then S(G) <m(G) + .

Proof By direct calculation, we haveS(P) =m(P) =  andS(P) =m(P) = . Using Lemmas . and ., we haveS(G)≤S(G– P) +S(P) < (m(G– P) + ) +m(P) = m(G) +  (orS(G)≤S(G– P) +S(P) < (m(G– P) + ) +m(P) =m(G) + ), this

completes the proof.

3 Proof of Theorem 1.3

First of all, using the facts thatS(G)≤m(G) +  for any graphGand thatBn=B∞n(p,q,l)∪

Bθ

n(p,q,l), we give the main idea of the proof.

. For each class, we show thatS(G) <m(G) + for the majority of graphs ofBn∞(p,q,l)

orBθ

n(p,q,l)by Lemma ..

. For the remaining graphs inB_n∞(p,q,l)orBθ

n(p,q,l)(except forGn+,n), we prove that S(G) <m(G) + by discussing case by case.

. We show thatS(Gn+,n) =m(Gn+,n) + , that is, the condition that equality holds. Next, we discuss according to the following two subsections.

3.1 Bicyclic graphs inB_n∞(p,q,l)

In this subsection, we prove thatS(G) <m(G) +  forG∈B∞n (p,q,l).

Lemma . Let G∈B∞_n(p,q,l).If(p,q,l)satisfies one of the following conditions:

() l≥,

() (p,q,l) = (p,q, )andq≥p≥, () (p,q,l) = (,q, )andq≥,

then S(G) <m(G) + .

Proof Direct calculation shows thatS(Cp∪Cq)≤m(Cp∪Cq), whereq≥p≥. For () l≥, using Lemmas . and ., we haveS(G)≤S(G–Cp–Cq) +S(Cp∪Cq) < (m(G– Cp–Cq) + ) +m(Cp∪Cq) =m(G) + , since each component ofG–Cp–Cqis tree. For both () and (), it is not difficult to check thatGhas  vertex-disjointP(or  vertex-disjoint P) such that each component ofG– P (orG– P) is a tree. Thus the result follows

from Lemma ..

By Lemma ., it suffices to consider the following two cases:G∈B∞_n(, , ) andG∈

B∞ n (, , ).

Lemma . For G∈B∞_n(, , ),we have S(G) <m(G) + . Proof ForG∈B_n∞(, , ), its kernel is∞(, , ), denoted byG

 for short shown in Fig-ure . LetV(G

Figure 3 Some bicyclic graphs with∞(3, 4, 0) as their kernel.

When{n,n, . . . ,n} ≥, if Gis not isomorphic toG shown in Figure , thenG has  vertex-disjointP (or  vertex-disjointP) such that each component ofG– P (orG– P) is a tree or a unicyclic graph of orderni which is not isomorphic toGni,ni.

Thus the result follows from Lemma .. IfGis isomorphic toG

, then we havemG()≥ n–  by Lemma .. Letλ≥λ≥ · · · ≥λ>λ=  be the other night eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculations, we haveλ+λ+λ≥μ(G) +μ(G) +μ(G) = . + . + . > , sinceG

containsGshown in Figure  as a subgraph. ThereforeS(G) =λ+λ<n+  = m(G) + .

If{n,n, . . . ,n}= , then we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other eight eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , sincei=n_i=μi= m(G).

Whenn= ,Gcontains a subgraph isomorphic toGi(i∈ {, , }) shown in Figure . By Lemma . and direct calculations, we haveλ+λ+λ≥μ(Gi) +μ(Gi) +μ(Gi) >  fori∈ {, , }. ThereforeS(G) =λ+λ<n+  =m(G) + .

Whenn≥, it can be checked thatmG()≥n–  by direct calculation and Lemma .. Letλ≥λ≥ · · · ≥λ>λ=  be the other seven eigenvalues ofG. Then we haveλ+ λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculations, we haveλ+λ≥μ(G) +μ(G) = , sinceGcontainsGas a subgraph. ThereforeS(G) = λ+λ<n+  =m(G) + .

If{n,n, . . . ,n}= , then we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other seven eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , sincei=n_i=μi= m(G). By Lemma . and direct calculation, we haveλ+λ≥μ(G) + μ(G) = , sinceGcontainsGas a subgraph. ThereforeS(G) =λ+λ<n+  =m(G) + . If{n,n, . . . ,n}= , thenGis isomorphic toG. Direct calculation shows thatS(G) < m(G) + .

The proof is completed.

Lemma . For G∈B∞_n(, , ),we have S(G) <m(G) + . Proof ForG∈B_n∞(, , ), its kernel is∞(, , ), denoted byG

for short shown in Fig-ure . LetV(G

) ={v, . . . ,v}. If there exists a vertexvi∈V(G) such thate(vi)≥, then it suffices to consider the case thatGis isomorphic toG

orGshown in Figure , otherwise Ghas  vertex-disjointP such that each component ofG– P is a tree and the result follows from Lemma ..

Figure 4 Some bicyclic graphs with∞(3, 3, 0) as their kernel.

μ(Hi) +μ(Hi) +μ(Hi) > , whereHi(i∈ {, }) is a subgraph ofGishown in Figure . ThereforeS(G) =λ+λ<n+  =m(G) + .

Now, it suffices to consider the case thatGis isomorphic toGshown in Figure . When{n,n, . . . ,n} ≥, if Gis isomorphic toG shown in Figure , thenGhas  vertex-disjointP (or  vertex-disjointP) such that each component ofG– P (or G– P) is a tree and the result follows from Lemma .. IfGis isomorphic toG, we havemG()≥n–  by direct calculation and Lemma .. Letλ≥λ≥ · · · ≥λ>λ=  be the other seven eigenvalues ofG. We haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculations we haveλ+λ≥μ(H) +μ(H) = . + . > , whereH

is a subgraph ofGshown in Figure . ThereforeS(G) =λ+λ<n+ =m(G)+. When{n,n, . . . ,n}= , it suffices to consider the case thatGis isomorphic toGi (i∈ {, , }) shown in Figure . WhenGis isomorphic to G

, we havemG()≥n–  by direct calculation and Lemma .. Let λ≥λ ≥ · · · ≥λ>λ=  be the other six eigenvalues ofG. We haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculations we haveλ+λ≥μ(H) +μ(H) = . + . > , whereH shown in Figure  is a subgraph ofG. ThereforeS(G) =λ+λ<n+  =m(G) + . When Gis isomorphic toGi_(i∈ {, }), we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other seven eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , sincei=n_i=μi= m(G). By Lemma . and direct calculations we haveλ+λ≥μ(Hi) + μ(Hi) > , whereHi shown in Figure  is a subgraph ofGi. ThereforeS(G) =λ+λ< n+  =m(G) + .

calculation, we haveφ(G_,λ) =λ(λ– )n–_{(λ– )}_{(λ–n). It follows thatS}

(G) =n+  < m+ .

If{n,n, . . . ,n}= , thenGis isomorphic toG. Direct calculation shows thatS(G) <

m(G) + .

We safely come to the following result by the above discussion.

Theorem . For G∈B_n∞(p,q,l),where q≥p≥and l≥,we have S(G) <m(G) + . 3.2 Bicyclic graphs inB_nθ(p,q,l)

In this subsection, we prove thatS(G)≤m(G) +  forG∈Bθn(p,q,l) and equality holds if and only if G∼= Gn+,n. We begin with the following lemma, which follows from Lemma . immediately.

Lemma . For G∈Bθ

n(p,q,l),if(p,q,l)satisfies one of the following conditions:

() ≤p≤q≤l,

() (p,q,l) = (,q,l)and≤q≤l, () (p,q,l) = (, ,l)and≤l,

then S(G) <m(G) + .

By Lemma ., it suffices to consider the following three cases: ()G∈Bθ

n(, , ), () G∈Bθ

n(, , ), and ()G∈Bnθ(,q,l), wherel≥q≥. First, we consider the caseG∈Bθ

n(, , ).

Lemma . For G∈Bθ

n(, , ),we have S(G) <m(G) + .

Proof ForG∈Bθ

n(, , ), its kernel isθ(, , ), denoted byGfor short shown in Figure . LetV(G_) ={v, . . . ,v}. If there exists a vertexviofGsuch thate(vi)≥, thenGhas  vertex-disjointP such that each component ofG– P is a tree and the result follows from Lemma .. Thus it suffices to consider the case thatGis isomorphic toGshown in Figure . Forn(G)≤, it is easy to check thatS(G) <m(G) +  by a direct calculation. Thus we assume thatn(G)≥ in the following.

If{n,n, . . . ,n} ≥, thenGhas  vertex-disjointP(or  vertex-disjointP) such that each component ofG– P(orG– P) is a tree and the result follows from Lemma .. If{n,n, . . . ,n} ≤, then we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other eight eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , sincei=n_i=μi= m(G). WhenGis not isomorphic toGshown in Figure , it contains a

subgraph which is isomorphic toGi_ (i∈ {, , }) shown in Figure . By Lemma . and direct calculations, we haveλ+λ+λ≥λ(Gi) +λ(Gi) +λ(Gi) >  fori∈ {, , }. ThereforeS(G) =λ+λ<n+  =m(G) + . WhenGis isomorphic toG, we havemG()≥ n–  by Lemma .. Letλ≥λ≥ · · · ≥λ>λ=  be the other seven eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculations, we haveλ+λ+λ≥μ(G) +μ(G) +μ(G) = . + . + . > , sinceGcontainsG

as a subgraph. ThereforeS(G) =λ+λ<n+  =m(G) + .

The proof is completed.

Second, we consider the caseG∈Bθ n(, , ).

Lemma . For G∈Bθ

n(, , ),we have S(G) <m(G) + .

Proof ForG∈Bθ

n(, , ), its kernel isθ(, , ), denoted byGfor short shown in Figure . Let V(G

) ={v, . . . ,v}. If there exists a vertex vi∈V(G) such thate(vi)≥, then by Lemma ., it suffices to consider the case thatGis isomorphic toG

orGshown in Figure .

WhenGis isomorphic toG_, we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other seven eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculation, we haveλ+λ+λ≥μ(H) + μ(H) +μ(H) = . + . + . > , whereHshown in Figure  is a subgraph ofG. ThereforeS(G) =λ+λ<n+  =m(G) + .

WhenGis isomorphic toG

, we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other nine eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , sincei=n_i=μi= m(G). Ifn≥ andn≥, thenGcontainsH shown in Figure  as a subgraph. By Lemma . and direct calculations, we haveλ+λ+λ+λ≥μ(H) + μ(H) +μ(H) +μ(H) = . + . + . + . > . ThereforeS(G) =λ+λ< n+  =m(G) + . Ifn=  orn= , then we have mG()≥n–  by Lemma .. Let λ≥λ≥ · · · ≥λ>λ=  be the other eight eigenvalues ofG. Then we haveλ+λ+

· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculation, we have

λ+λ+λ≥μ(H) +μ(H) +μ(H) = . + . + . > , whereH shown in Figure  is a subgraph ofG

. ThereforeS(G) =λ+λ<n+  =m(G) + . Now, we consider the case thatGis isomorphic toGshown in Figure .

First, we consider the case that{n,n, . . . ,n} ≥. IfGis not isomorphic toGshown in Figure , thenGhas  vertex-disjointP(or  vertex-disjointP) such that each compo-nent ofG–P(orG–P) is a tree and the result follows from Lemma .. WhenGis iso-morphic toG

, we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥λ>λ=  be the other eight eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+, since

i=n

i=μi= m(G). By Lemma . and direct calculation, we haveλ+λ+λ≥μ(H) +μ(H) +μ(H) > . + . + . > , where H

 shown in Figure  is a subgraph of G. Therefore S(G) =λ+λ<n+  =m(G) + .

When{n,n, . . . ,n}= , we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other seven eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , sincei=n_i=μi= m(G). Then by Lemma . and direct calculations, we haveλ+λ≥ μ(Hi) +μ(Hi)≥ (i∈ {, }), whereHi (i∈ {, }) shown in Figure  is a subgraph of G. ThereforeS(G) =λ+λ<n+  =m(G) + .

When{n,n, . . . ,n}= , we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other six eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , sincei=n_i=μi= m(G). By Lemma . and direct calculation, we haveλ+λ≥μ(G) + μ(G) = . + . = , sinceGcontainsGas a subgraph. ThereforeS(G) =λ+λ< n+  =m(G) + , as required.

When{n,n, . . . ,n}= ,Gis isomorphic toG. Direct calculation shows thatS(G) < m(G) + .

From the above discussion, we complete the proof.

Finally, we consider the caseG∈Bθ

n(,q,l), wherel≥q≥. Lemma . If G∈Bθ

n(,q,l)with l≥q≥,then S(G) <m(G) + .

Proof Ifq≥, it is obviously thatGhas  vertex-disjointPsuch thatG– Pis a forest and the result follows immediately from Lemma .. Whenq=  andl≥, the result follows immediately from Lemma ., sinceGhas  vertex-disjointPsuch thatG– P is a forest. Thus it suffices to consider the case thatG∈Bθ

n(, , ). ForG∈Bθ

n(, , ), its kernel isθ(, , ), denoted byGfor short shown in Figure . LetV(G_) ={v, . . . ,v}. If there exists a vertexvi∈V(G) such thate(vi)≥, thenGhas  vertex-disjointPsuch that each component ofG– Pis a tree and the result follows from Lemma .. Now, it suffices to consider the case thatGis isomorphic toGshown in Figure .

When{n,n, . . . ,n} ≥,Ghas  vertex-disjointP(or  vertex-disjointP) such that each component ofG– P(orG– P) is a tree and the result follows from Lemma .. When ≤ {n,n, . . . ,n} ≤, we havemG()≥n–  by Lemma .. Letλ≥λ≥

· · · ≥λ>λ=  be the other eight eigenvalues ofG. Then we haveλ+λ+· · ·+λ= n+ , sincei=n_i=μi= m(G). If Gis not isomorphic toG shown in Figure , thenG contains a subgraph which is isomorphic to G

Figure 7 Some bicyclic graphs withθ(2, 4, 4) as their kernel.

Figure 8 Some bicyclic graphs withθ(2, 3, 5) as their kernel.

mG() =n–  by direct calculation and Lemma .. Letλ≥λ≥ · · · ≥λ>λ=  be the other six eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculation, we haveλ+λ≥μ(G) +μ(G) = . + . > , sinceG

containsGas a subgraph. ThereforeS(G) =λ+λ<n+  =m(G) + . When{n,n, . . . ,n}= ,Gis isomorphic toG. Direct calculation shows thatS(G) < m(G) + .

The proof is completed.

Lemma . If G∈Bθ

n(, ,l)with l≥,then S(G) <m(G) + .

Proof Whenl≥, it is obviously thatGhas  vertex-disjointPsuch thatG– Pis a forest and the result follows immediately from Lemma .. Thus it suffices to consider the case thatG∈Bθ

n(, , ). Forn(G)≤, it is easy to check thatS(G) <m(G) +  by a direct calculation. Thus we assume thatn(G)≥ in the following.

ForG∈Bθ

n(, , ), its kernel isθ(, , ), denoted byGfor short shown in Figure . LetV(G

) ={v, . . . ,v}. If there exists a vertexviofGsuch thate(vi)≥, thenGhas  vertex-disjointPsuch thatG– Pis a forest and the result follows from Lemma .. Now, we can assume thatGis isomorphic toGshown in Figure .

If{n,n, . . . ,n} ≥, thenGhas  vertex-disjointP(or  vertex-disjointP) such that each component ofG– P(orG– P) is a tree and the result follows from Lemma .. If{n,n, . . . ,n} ≤, then we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ >λ =  be the other eight eigenvalues of G. We have λ+λ +· · ·+λ =n+ , since i=n_i=μi = m(G). Note that G contains a subgraph which is isomorphic to Gi (i∈ {, , , , }) shown in Figure . By Lemma . and direct calculations, we have λ+λ+λ≥μ(Gi) +μ(Gi) +μ(Gi) >  (i∈ {, , , , }). ThereforeS(G) =λ+λ< n+  =m(G) + .

Figure 9 Some bicyclic graphs withθ(2, 3, 4) as their kernel.

Lemma . For G∈Bθ

n(, , ),we have S(G) <m(G) + .

Proof ForG∈Bθ

n(, , ), its kernel isθ(, , ), denoted byGfor short shown in Figure . LetV(G_) ={v, . . . ,v}.

If there exists a vertexvisuch thate(vi)≥, then by Lemma ., it suffices to consider the cases thatGis isomorphic toGi

(i∈ {, , }) shown in Figure . WhenGis isomorphic toGi

(i∈ {, , }) shown in Figure , we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥λ>λ=  be the other seven eigenvalues ofG. We have λ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculations, we haveλ+λ+λ≥μ(Hi) +μ(Hi) +μ(Hi) > , whereHi shown in Figure  is a subgraph ofGi_. ThereforeS(G) =λ+λ<n+  =m(G) + .

Now, it suffices to consider the case thatGis isomorphic toGshown in Figure . For n(G)≤, it is easy to check thatS(G) <m(G) +  by a direct calculation. In the following, we assume thatn(G)≥.

If{n,n, . . . ,n} ≥, thenGhas  vertex-disjointP(or  vertex-disjointP) such that each component ofG– P(orG– P) is a tree and the result follows from Lemma .. If{n,n, . . . ,n}= , then we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other seven eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , sincei=n_i=μi= m(G). IfGis not isomorphic toGshown in Figure , then it contains a subgraph isomorphic toHi

(i∈ {, . . . , }) shown in Figure . By Lemma . and direct calculations, we haveλ+λ≥μ(Gi) +μ(Gi) >  (i∈ {, . . . , }). ThereforeS(G) = λ+λ<n+  =m(G) + . WhenGis isomorphic toG, we havemG()≥n–  by direct calculation and Lemma .. Letλ≥λ≥ · · · ≥λ>λ=  be the other six eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculations, we haveλ+λ≥μ(H) +μ(H) > , whereHshown in Figure  is a subgraph ofG

. ThereforeS(G) =λ+λ<n+  =m(G) + .

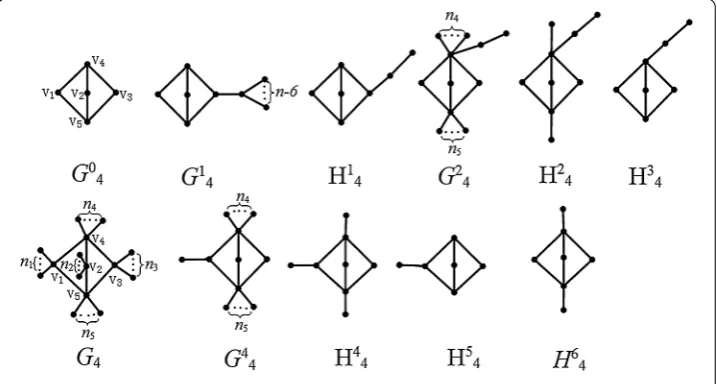
Figure 10 Some bicyclic graphs withθ(2, 3, 3) as their kernel.

μ(Hi) >  (i∈ {, , }), where Hi shown in Figure  is a subgraph ofG. Therefore S(G) =λ+λ<n+  =m(G) + .

The proof is completed.

Lemma . Let G∈Bθ

n(, , )and Gshown in Figurebe the kernel of G.If there exists a vertex viof Gsuch that e(vi)≥,then S(G) <m(G) + .

Proof By Lemma ., it suffices to consider the case thatG is isomorphic toGi (i∈

{, , }) shown in Figure .

WhenGis isomorphicGi(i∈ {, , }), we havemG()≥n–  by Lemma .. Letλ≥ λ≥ · · · ≥λ>λ=  be the other eight eigenvalues ofGi. We haveλ+λ+· · ·+λ= n+ , sincei=n_i=μi= m(G). By Lemma . and direct calculations, we haveλ+λ+λ≥ μ(Gi) +μ(Gi) +μ(Gi) > , whereGishown in Figure  is the subgraph ofGi. Therefore S(G) =λ+λ<n+  =m(G) + .

The proof is completed.

Lemma . Let G ∈ Bθ

n(, , ) and G shown in Figure  be the kernel of G. If maxi=

i=e(vi) = ,then S(G) <m(G) + ,where viis the vertices of G.

Proof By Lemma ., it suffices to consider the case thatGis isomorphic toGorG shown in Figure . Here, we only prove the case thatGis isomorphic toG. For the case Gis isomorphic toG, we can discuss similarly.

When{n,n,n,n} ≥,Ghas  vertex-disjointP(or  vertex-disjointP) such that each component ofG– P(orG– P) is a tree and the result follows from Lemma .. When{n,n,n,n} ≤, we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥ λ>λ=  be the other seven eigenvalues ofG. We haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). By Lemma . and direct calculations, we have λ+λ≥μ(G) + μ(G) = . + . = , where G shown in Figure  is a subgraph of G. Thus

S(G) <m(G) + .

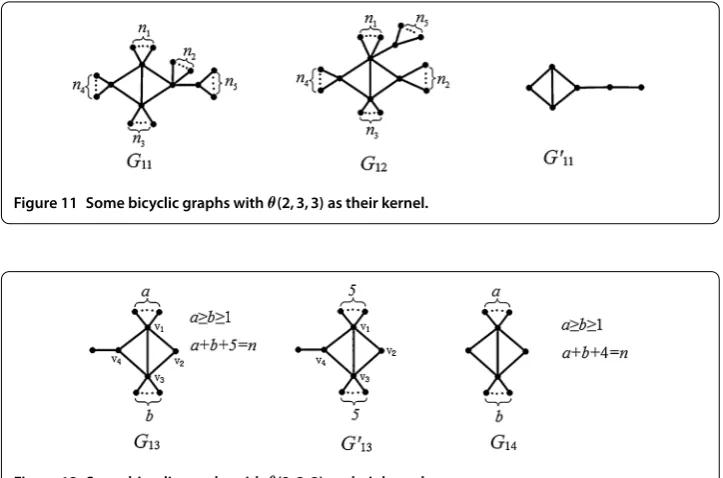
Lemma . Let Gbe the bicyclic graph of order n shown in Figure,where a≥b≥ and a+b+  =n.Then S(G) <m(G) + .

Proof Forn(G)≤, it is easy to check thatS(G) <m(G) +  by a direct calculation. In following, we assume thatn(G)≥.

Ifb≥, thenGcontainsGshown in Figure  as a subgraph. Note thatmG()≥ n–  by Lemma .. Letλ≥λ≥ · · · ≥λ>λ=  be the other seven eigenvalues of G. We haveλ+λ+· · ·+λ=n+ , since

i=n

Figure 11 Some bicyclic graphs withθ(2, 3, 3) as their kernel.

Figure 12 Some bicyclic graphs withθ(2, 3, 3) as their kernel.

Ifb= , then we haveλ(G) <+  =n–  by Lemma . andλ(G) <λ(Lv(G)) = . by Lemma . and direct calculation. It follows thatS(G) <n+  =m(G) + .

Ifb= , then we haveλ(G) <+  =n–  by Lemma . andλ(G) <λ(Lv(G)) = . by Lemma . and direct calculation. It follows thatS(G) <n+  =m(G) + .

Ifb= , then we haveλ(G) < (n– ) +n+_n–by Lemma . andλ(G) <λ(Lv(G)) = . < . by Lemma . and direct calculation. ThereforeS(G) <n–  +n+_n–+ . < n+  =m(G) + .

Ifb= , then we haveλ(G) < (n– ) +n+_n– by Lemma . andλ(G) <λ(Lv(G)) = . < . by Lemma . and direct calculation. ThusS(G) <n–  +n+_n–+ . <n+  =

m(G) + .

Lemma . Let Gbe the bicyclic graph of order n shown in Figure,where a≥b≥ and a+b+  =n.Then S(G) <m+ .

Proof By some elementary calculations, we haveφ(G,x) =x(x– )(x– )g(x), where g(x) =x_{– (n+ )x}_{+ (n+ab+ )x}_{– (n+ ab+ )x+ n. Letx}

≥x≥x≥xbe the roots ofg(x) = . Then

x+x+x+x=n+ , (.)

xx+xx+xx+xx+xx+xx= n+ab+ , (.)

xxx+xxx+xxx+xxx= n+ ab+ . (.)

If

then, by (.), we have

x+x= . (.)

From (.)-(.) follows that

xx+xx= n+ab+ , (.)

(n+ )xx+ xx= n+ ab+ . (.)

By (.) and (.), we have

xx= . (.)

Combining (.) and (.), we have

x=x= . (.)

Then g() = –ab= , which implies thatb= . Therefore,b≥ implies thatS(G) <

m(G) + .

Lemma . Let G be the bicyclic graph of order n shown in Figure,where a≥b≥, c≥d≥and a+b+c+d+  =n.Then S(G)≤m+ with equality if and only if a=n–  and b=c=d=  (that is,G∼=Gn+,n).

Proof Forn(G)≤, it is easy to check thatS(G)≤m(G) +  with equality if and only if G∼=Gn+,nby a direct calculation. In the following, we assume thatn(G)≥.

When{a,b,c,d}= , we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥λ> λ=  be the other eight eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G).

If c≥, then GcontainsH shown in Figure  as a subgraph. By Lemma . and direct calculations, we have λ +λ≥μ(H) +μ(H) = . + . > . If c=d=  andb≥, thenGcontainsH shown in Figure  as a subgraph. By Lemma . and direct calculations, we have λ+λ≥μ(H) +μ(H) = . + . > . Therefore S(G) = λ +λ <n+  =m(G) + . Now, we can assume that b =c=d= . Under

the assumption, Gis isomorphic to H shown in Figure . We haveλ(H) <n–  by Lemma . andλ(H) <λ(Lv(H)) = . by Lemma . and direct calculation. There-fore,S(G) < (n– ) + . <n+  =m(G) + .

When{a,b,c,d}= , we havemG()≥n–  by Lemma .. Letλ≥λ≥ · · · ≥λ> λ=  be the other seven eigenvalues ofG. Then we haveλ+λ+· · ·+λ=n+ , since

i=n

i=μi= m(G). IfGis isomorphic toG, thenS(G) <m(G) +  by Lemma .. Other-wise it contains a subgraph isomorphic toHi(i∈ {, , , }) shown in Figure . Then we haveλ+λ≥λ(Hi) +λi(Hi) >  (i∈ {, , , }) by Lemma . and direct calculations. ThereforeS(G) =λ+λ<n+  =m(G) + .

When{a,b,c,d}= ,Gis isomorphic toGshown in Figure  orHi (i∈ {, }) shown in Figure . For G is isomorphic to G, we have S(G) < m(G) +  by Lemma .. ForGis isomorphic toH(orH), we havemG()≥n–  by Lemma .. Let λ ≥λ ≥ · · · ≥λ >λ=  be the other six eigenvalues of H (or H). We have λ +λ +· · ·+λ=n+ , since i=ni=μi= m(G). Note thatH containsH as a sub-graph (HcontainsHorHas a subgraph), whereHi(i= , , ) shown in Figure . By Lemma . and direct calculations, we haveλ+λ≥μ(Hi) +μ(Hi) >  (i= , , ). ThereforeS(G) =λ+λ<n+  =m(G) + , as required. When {a,b,c,d}= ,Gis isomorphic toHorGn+,n. We haveλ(H) <nby Lemma . andλ(H) =  by di-rect calculations. It follows thatS(H) <n+ . ForGn+,n, a direct calculation shows that

S(Gn+,n) =m+ .

From the discussion above, we safely come to the following result.

Theorem . For G∈Bθ

n(p,q,l),where l≥q≥p≥and at most one of them is,we have S(G)≤m(G) + and the equality holds if and only if G∼=Gn+,n.

Theorem . follows immediately from Theorems . and ..

Competing interests

The authors declare that they have no competing interests.

Authors’ contributions

YRZ carried out the proofs of main results in the manuscript. AC, JXL and SR participated in the design of the study and drafted the manuscripts. All the authors read and approved the final manuscripts.

Author details

1_{School of Applied Mathematics, Xiamen University of Technology, Xiamen, Fujian, P.R. China.}2_{Center for Discrete}

Mathematics, Fuzhou University, Fuzhou, Fujian, P.R. China. 3_{School of Mathematics and Statistics, Minnan Normal} University, Zhangzhou, Fujian, P.R. China.

Acknowledgements

The authors would like to thank the anonymous referees for their constructive corrections and valuable comments on this paper, which have considerably improved the presentation of this paper. This project is supported by NSF of China (Nos. 11471077, 11301440), the Foundation to the Educational Committee of Fujian (JA13240, JA15381).

Received: 16 July 2016 Accepted: 8 November 2016

References

1. Guan, M, Zhai, M, Wu, Y: On the sum of two largest Laplacian eigenvalue of trees. J. Inequal. Appl.2014, 242 (2014) 2. Fiedler, M: Algebraic connectivity of graphs. Czechoslov. Math. J.23, 298-305 (1973)

3. Anderson, W, Morley, T: Eigenvalues of the Laplacian of a graph. Linear Multilinear Algebra18, 141-145 (1985) 4. Brouwer, A, Haemers, W: Spectra of Graphs. Springer, New York (2012)

5. Guo, J-M: On the second largest Laplacian eigenvalue of trees. Linear Algebra Appl.404, 251-261 (2005)

6. Li, J, Guo, J-M, Shiu, WC: On the second largest Laplacian eigenvalue of graphs. Linear Algebra Appl.438, 2438-2446 (2013)

7. Liu, M, Liu, B, Cheng, B: Ordering (signless) Laplacian spectral radii with maximum degree of graphs. Discrete Math.

8. Merris, R: A note on the Laplacian graph eigenvalues. Linear Algebra Appl.285, 33-35 (1990)

9. Zhang, X-D, Li, J: The two largest Laplacian eigenvalue of trees. J. Univ. Sci. Technol. China28, 513-518 (1998) 10. Haemers, W, Mohammadian, A, Tayfeh-Rezaie, B: On the sum of Laplacian eigenvalues of graphs. Linear Algebra Appl.

432, 2214-2221 (2010)

11. Du, Z, Zhou, B: Upper bounds for the sum of Laplacian eigenvalues of graphs. Linear Algebra Appl.436, 3672-3683 (2012)

12. Rocha, I, Trevisian, V: Bounding the sum of the Laplacian graph eigenvalues of graphs. Discrete Appl. Math.170, 95-103 (2014)

13. Wang, S, Huang, Y, Liu, B: On the conjecture for the sum of the Laplacian graph eigenvalues. Math. Comput. Model.

56, 60-68 (2012)

14. Fritscher, E, Hoppen, C, Rocha, I, Trevisan, V: On the sum of the Laplacian eigenvalues of a tree. Linear Algebra Appl.

435, 371-399 (2011)

15. Zheng, Y, Chang, A, Li, J: On the sum of two largest Laplacian eigenvalue of unicyclic graphs. J. Inequal. Appl.2015, 275 (2015)

16. Fan, K: On a theorem of wely concerning eigenvalues of linear transformations. Proc. Natl. Acad. Sci. USA35, 652-655 (1949)