Some approximation properties of \((p,q)\) Bernstein operators

R E S E A R C H

Open Access

Some approximation properties of

(

p

,

q

)-Bernstein operators

Shin Min Kang

_{, Arif Rafiq}

_{, Ana-Maria Acu}

_{, Faisal Ali}

_{and Young Chel Kwun}

*_{Correspondence:} yckwun@dau.ac.kr

5_{Department of Mathematics,} Dong-A University, Busan, 49315, Korea

Full list of author information is available at the end of the article

Abstract

This paper is concerned with the (p,q)-analog of Bernstein operators. It is proved that, when the function is convex, the (p,q)-Bernstein operators are monotonic decreasing, as in the classical case. Also, some numerical examples based on Maple algorithms that verify these properties are considered. A global approximation theorem by means of the Ditzian-Totik modulus of smoothness and a Voronovskaja type theorem are proved.

MSC: 41A10; 41A25; 41A35

Keywords: (p,q)-Bernstein operators; (p,q)-calculus; Voronovskaja type theorem; K-functional; Ditzian-Totik first order modulus of smoothness

1 Introduction and preliminaries

During the last decade, the applications ofq-calculus in the field of approximation theory

has led to the discovery of new generalizations of classical operators. Lupaş [] was first to

observe the possibility of usingq-calculus in this context. For more comprehensive details

the reader should consult monograph of Aralet al.[] and the recent references [–].

Nowadays, the generalizations of several operators in post-quantum calculus, namely the (p,q)-calculus have been studied intensively. The (p,q)-calculus has been used in many areas of sciences, such as oscillator algebra, Lie group theory, field theory, differential

equations, hypergeometric series, physical sciences (see [, ]). Recently, Mursaleenet

al.[] defined (p,q)-analog of Bernstein operators. The approximation properties for

these operators based on Korovkin’s theorem and some direct theorems were considered. Also, many well-known approximation operators have been introduced using these tech-niques, such as Bleimann-Butzer-Hahn operators [] and Szász-Mirakyan operators [].

In the present paper, we prove new approximation properties of (p,q)-analog of

Bern-stein operators. First of all, we recall some notations and definitions from the (p,q

)-calculus. Let  <q<p≤. For each non-negative integer n≥k≥, the (p,q)-integer [k]p,q, (p,q)-factorial [k]p,q!, and (p,q)-binomial are defined by

[k]p,q:=

pk_–qk

p–q ,

[k]p,q! :=

⎧ ⎨ ⎩

[k]p,q[k– ]p,q· · ·[]p,q, k≥,

, k= ,

and

n k

p,q

:= [n]p,q! [n–k]p,q![k]p,q!

.

As a special case whenp= , the above notations reduce toq-analogs.

The (p,q)-power basis is defined as

(xa)n_p,q= (x–a)(px–qa)px–qa· · ·pn–x–qn–a. The (p,q)-derivative of the functionf is defined as

Dp,qf(x) =

f(px) –f(qx)

(p–q)x , x= .

Letf be an arbitrary function anda∈R. The (p,q)-integral off on [,a] is defined as

a



f(t)dp,qt= (q–p)a

∞

k=

f

pk

qk+a

pk

qk+, if

p_q< ,

a



f(t)dp,qt= (p–q)a

∞

k=

f

qk pk+a

qk pk+, if

q_p< .

The (p,q)-analog of Bernstein operators forx∈[, ] and  <q<p≤ are introduced as follows:

Bp_n,q(f;x) =

n

k=

bp_n,_,q_k(x)f

pn–k[k]p,q

[n]p,q

,

where the (p,q)-Bernstein basis is defined as

bp_n,_,q_k(x) =

n k

p,q

p[k(k–)–n(n–)]/xk(x)n_p–_,qk.

Lemma . For x∈[, ],  <q<p≤,we have

B_np,q(e;x) = , Bnp,q(e;x) =x,

Bp_n,q(e;x) =

pn–

[n]p,q

x+q[n– ]p,q [n]p,q

x,

where ei(x) =xiand i∈ {, , }.

Lemma . Let n be a given natural number,then

Bp_n,q(t–x);x= p

n–

[n]p,q

φ(x)≤  [n]p,q

φ(x),

2 Monotonicity for convex functions

Oru and Phillips [] proved that when the functionf is convex on [, ], itsq-Bernstein

operators are monotonic decreasing. In this section we will study the monotonicity of (p,q)-Bernstein operators.

Theorem . If f is convex function on[, ],then

Bp_n,q(f;x)≥f(x), ≤x≤,

for all n≥and <q<p≤.

Proof We consider the knotsxk=p

n–k_[k] p,q

[n]p,q ,λk=

n k

p,qp

[k(k–)–n(n–)]/_xk_(x)n–k

p,q, ≤k≤n.

Using Lemma ., it follows that

λ+λ+· · ·+λn= ,

xλ+x+λ+· · ·+xnλn=x.

From the convexity of the functionf, we get

Bp_n,q(f;x) =

n

k=

λkf(xk)≥f

_n

k=

λkxk

=f(x).

Example . Letf :R→R,f(x) =xex+_{. Figure  illustrates thatB}p,q

n (f;x)≥f(x) for the

convex functionf andx∈[, ].

Theorem . Let f be convex on[, ].Then Bp_n,_–q(f;x)≥Bnp,q(f;x)for <q<p≤, ≤

x≤,and n≥.If f ∈C[, ]the inequality holds strictly for <x< unless f is linear in each of the intervals between consecutive knots pn_[––_n–]k[k]p,q

p,q , ≤k≤n– ,in which case we

have the equality.

Proof For  <q<p≤ we begin by writing

n–

s=

ps–qsx–Bp_n,_–q(f;x) –Bp_n,q(f;x)

=

n–

s=

ps–qsx–

_n–

k=

n– 

k

p,q

p[k(k–)–(n–)(n–)]/xk(x)n_p–_,qk–f

pn––k_[k]

[n– ]

– n– k= n k

p,q

p[k(k–)–n(n–)]/xk(x)n_p–_,qkf

pn–k[k] [n]

= n– k=

n– 

k

p,q

p[k(k–)–(n–)(n–)]/xk

n–

s=n–k–

ps–qsx–f

pn––k_[k]

[n– ]

– n k= n k

p,q

p[k(k–)–n(n–)]/xk

n–

s=n–k

ps–qsx–f

pn–k_[k]

[n]

.

Denote

k(x) =p

k(k–)  _xk

n–

s=n–k

ps–qsx–, (.)

and using the following relation:

pn–pk(k–)_xk

n–

s=n–k–

ps–qsx–=pkk(x) +qn–k–k+(x),

we find

n–

s=

ps–qsx–Bp_n,_–q(f;x) –Bp_n,q(f;x)

=

n–

k=

n– 

k

p,q

p–(n–)(n–)_p–(n–)_pk_{k(x) +q}n–k–_k+(x)f

pn––k[k]p,q

[n– ]p,q

– n k= n k

p,q

p–n(n–)

k(x)f

pn–k_[k] p,q

[n]p,q

=p–n(n–)

_n–

k=

n– 

k

p,q

pkk(x)f

pn––k_[k] p,q

[n– ]p,q

+ n k=

n– 

k– 

p,q

qn–kk(x)f

pn–k_{[k– ]} p,q

[n– ]p,q

– n k= n k k(x)f

pn–k_[k] p,q

[n]p,q

=p–n(n–)

n–

k=

n– 

k

p,q

pkf

pn––k_[k] p,q

[n– ]p,q

+

n– 

k– 

p,q

qn–kf

pn–k_{[k– ]} p,q

[n– ]p,q

– n k

p,q

f

pn–k[k]p,q

[n]p,q

=p–n(n–)

n–

k=

n k

p,q

[n–k]p,q

[n]p,q

pkf

pn––k_[k] p,q

[n– ]p,q

+[k]p,q [n]p,q

qn–kf

pn–k[k– ]p,q

[n– ]p,q

–f

pn–k[k]p,q

[n]p,q

k(x)

=p–n(n–)

n–

k=

n k

p,q

akk(x),

where

ak=

[n–k]p,q

[n]p,q

pkf

pn––k[k]p,q

[n– ]p,q

+[k]p,q [n]p,q

qn–kf

pn–k[k– ]p,q

[n– ]p,q

–f

pn–k[k]p,q

[n]p,q

.

From (.) it is clear that eachk(x) is non-negative on [, ] for  <q<p≤ and, thus, it

suffices to show that eachakis non-negative.

Sincef is convex on [, ], then for anyt,t∈[, ] andλ∈[, ], it follows that

fλt+ ( –λ)t

≤λf(t) + ( –λ)f(t).

If we chooset=p

n–k_[k–] p,q

[n–]p,q ,t=

pn––k[k]p,q

[n–]p,q , andλ=

[k]p,q

[n]p,qq

n–k_{, thent}

,t∈[, ] andλ∈

(, ) for ≤k≤n– , and we deduce that

ak=λf(t) + ( –λ)f(t) –f

λt+ ( –λ)t

≥.

ThusBpn,–q(f;x)≥B

p,q n (f;x).

We have equality forx=  andx= , since the Bernstein polynomials interpolatef on

these end-points. The inequality will be strict for  <x<  unless whenf is linear in each of the intervals between consecutive knots pn––k[k]p,q

[n–]p,q , ≤k≤n– , then we haveB

p,q n–(f;x) =

Bpn,q(f;x) for ≤x≤.

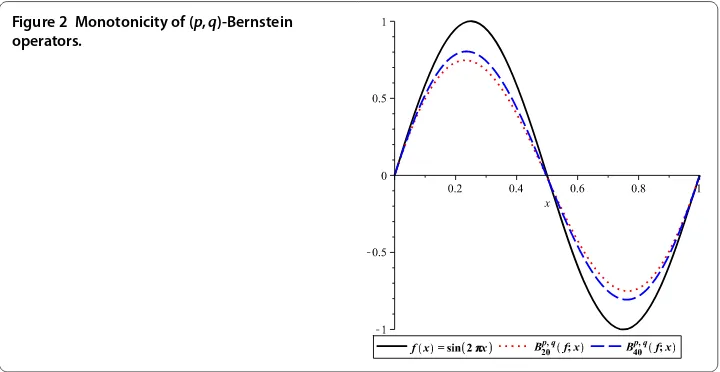
Example . Letf(x) =sin(πx),x∈[, ]. Figure  illustrates the monotonicity of (p,q

)-Bernstein operators forp= . andq= .. We note that iff is increasing (decreasing)

on [, ], then the operators is also increasing (decreasing) on [, ].

3 A global approximation theorem

In the following we establish a global approximation theorem by means of Ditzian-Totik modulus of smoothness. In order to prove our next result, we recall the definitions of the

Ditzian-Totik first order modulus of smoothness and theK-functional []. Letφ(x) =

√

x( –x) andf ∈C[, ]. The first order modulus of smoothness is given by

ωφ(f;t) = sup

<h≤t

f

x+hφ(x) 

–f

x–hφ(x) 

,x±hφ(x)

 ∈[, ]

. (.)

The correspondingK-functional to (.) is defined by

Kφ(f;t) = inf g∈Wφ[,]

f –g+tφg (t> ),

whereWφ[, ] ={g:g∈ACloc[, ],φg<∞}andg∈ACloc[, ] means thatgis

abso-lutely continuous on every interval [a,b]⊂[, ]. It is well known ([], p.) that there exists a constantC>  such that

Kφ(f;t)≤Cωφ(f;t). (.)

Theorem . Let f ∈C[, ]andφ(x) =√x( –x),then for every x∈[, ],we have

Bp_n,q(f;x) –f(x)≤Cωφ

f;  [n]p,q

,

where C is a constant independent of n and x.

Proof Using the representation

g(t) =g(x) +

t x

g(u)du,

we get

Bp_n,q(g;x) –g(x)=Bp_n,q

t x

g(u)du;x. (.)

For anyx∈(, ) andt∈[, ] we find that

_xtg(u)du≤φg

t x



φ(u)du

. (.)

Further,

_xt _φ(_u)du=

t x

 √

u( –u)du

≤ t

x

 √

u+

 √

 –u

du

= |t–x|

 √

t+√x+

 √

 –t+√ –x

< |t–x|

 √

x+

 √

 –x

≤ √

|t–x|

φ(x) . (.)

From (.)-(.) and using the Cauchy-Schwarz inequality, we obtain

Bp_n,q(g;x) –g(x)< √φgφ–(x)B_np,q|t–x|;x

≤√φgφ–(x)B_np,q(t–x);x/.

Using Lemma ., we get

_Bp,q

n (g;x) –g(x)≤

√

[n]p,q

φg.

Now, using the above inequality we can write

Bp_n,q(f;x) –f(x)≤Bp_n,q(f –g;x)+f(x) –g(x)+Bp_n,q(g;x) –g(x)

≤√

f–g+  [n]p,q

φg

.

Taking the infimum on the right-hand side of the above inequality over allg∈Wφ[, ],

we get

Bp_n,q(f;x) –f(x)≤CKφ

f;  [n]p,q

.

Using equation (.) this theorem is proven.

4 Voronovskaja type theorem

Using the first order Ditzian-Totik modulus of smoothness, we prove a quantitative

Voronovskaja type theorem for the (p,q)-Bernstein operators.

Theorem . For any f ∈C_{[, ]the following inequalities hold:}

(i) |[n]p,q[Bnp,q(f;x) –f(x)] –p

n–_φ_(x)

 f(x)| ≤Cωφ(f,φ(x)n–/),

(ii) |[n]p,q[Bnp,q(f;x) –f(x)] –p

n–_φ_(x)

 f(x)| ≤Cφ(x)ωφ(f,n–/),

where C is a positive constant.

Proof Letf ∈C_{[, ] be given andt,x∈[, ]. Using Taylor’s expansion, we have}

f(t) –f(x) = (t–x)f(x) +

t x

(t–u)f(u)du.

Therefore,

f(t) –f(x) – (t–x)f(x) –  (t–x)

_{f(x) =} t

x

(t–u)f(u)du–

t x

(t–u)f(x)du

=

t x

In view of Lemma . and Lemma ., we get

Bp_n,q(f;x) –f(x) – p

n–

[n]p,q

φ(x)f(x)≤Bp_n,q

t x

|t–u|f(u) –f(x)du;x

. (.)

The quantity|_xt|f(u) –f(x)||t–u|du|was estimated in [], p., as follows:

t

x

_{f(u) –f(x)|t–u|du≤f–g(t–x)}_{+ φgφ}–_(x)|t–x|_{, (.)}

whereg∈Wφ[, ]. On the other hand, for anym= , , . . . and  <q<p≤, there exists a

constantCm>  such that

Bp_n,q(t–x)m_p,q;x≤Cm

φ_(x)

[n] m+



p,q

, (.)

wherex∈[, ] andais the integer part ofa≥.

Throughout this proof,Cdenotes a constant not necessarily the same at each

occur-rence.

Now, combining (.)-(.) and applying Lemma ., the Cauchy-Schwarz inequality, we get

Bp_n,q(f;x) –f(x) –p

n–_φ_(x)

[n]p,q

f(x)

≤f–gB_np,q(t–x);x+ φgφ–(x)B_np,q|t–x|;x

≤f–gφ

_(x)

[n]p,q

+ φgφ–(x)Bp_n,q(t–x);x/Bp_n,q(t–x);x/

≤f–gφ

_(x)

[n]p,q

+  C

[n]p,q

φgφ(x)

[n]p,q

≤ C

[n]p,q

φ(x)f–g+ [n]–/_p,q φ(x)φg.

Sinceφ_{(x)≤φ(x)≤,x∈[, ], we obtain}

[n]p,q

Bp,q

n (f;x) –f(x)

–p

n–_φ_(x)

 f

_{(x)≤Cf–g+ [n]}–/

p,q φ(x)φg.

Also, the following inequality can be obtained:

[n]p,q

Bp_n,q(f;x) –f(x)–p

n–_φ_(x)

 f

_{(x)≤Cφ(x)f–g+ [n]}–/

p,q φg.

Taking the infimum on the right-hand side of the above relations overg∈Wφ[, ], we get

[n]p,q

Bp_n,q(f;x) –f(x)–p

n–_φ_(x)

 f

_(x)≤

CKφ(f;φ(x)[n]–/p,q ),

Cφ(x)Kφ(f; [n]–/p,q ).

(.)

5 Better approximation

In , King [] proposed a technique to obtain a better approximation for the well-known Bernstein operators as follows:

(Bnf)◦rn

(x) =

n

k=

f

k n

n k

rn(x)

k

 –rn(x)

n–k

, (.)

where rnis a sequence of continuous functions defined on [, ] with ≤rn(x)≤ for

eachx∈[, ] andn∈ {, , . . .}. The modified Bernstein operators (.) preserveeand

e and present a degree of approximation at least as good. In [], the authors consider

the sequence of linear Bernstein-type operators defined forf ∈C[, ] byBn(f◦τ–)◦τ,τ

being any function that is continuously differentiable∞times on [, ], such thatτ() = ,

τ() = , andτ(x) >  forx∈[, ].

So, using the technique proposed in [], we modify the (p,q)-Bernstein operators as

follows:

Bp_n,q(f;x) =

n

k=

bp_n,_,q_k(x)f◦τ–p

n–k_[k] p,q

[n]p,q

,

where

bp_n,q(x) =

n k

p,q

p[k(k–)–n(n–)]/τ(x)kτ(x)n_p–_,qk.

Then we have

Bp_n,q(e;x) = , B

p,q n

τ(t);x=τ(x),

Bp_n,qτ(t);x= p

n–

[n]p,q

τ(x) +q[n– ]p,q [n]p,q

τ(x),

Bp_n,qτ(t) –τ(x);x= p

n–

[n]p,q

φ_τ(x),

whereφ_τ(x) :=τ(x)( –τ(x)).

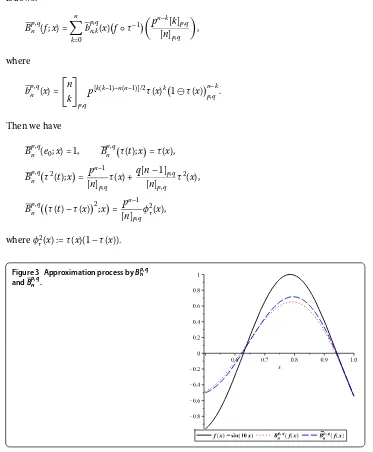
Figure 3 Approximation process byBpn,q

Example . We compare the convergence of (p,q)-analog of Bernstein operatorsBpn,qf

with the modified operators Bp_n,qf. We have considered the functionf(x) =sin(x) and

τ(x) =x_+x. Forx∈[_, ],p= .,q= .,n= , the convergence of the operatorsBpn,q

andBp_n,qto the functionf is illustrated in Figure . Note that the approximation byBp_n,qf

is better than using (p,q)-Bernstein operatorsBpn,qf.

Competing interests

The authors declare that they have no competing interests.

Authors’ contributions

All authors read and approved the final manuscript.

Author details

1_{Department of Mathematics and RINS, Gyeongsang National University, Jinju, 52828, Korea.}2_{Department of} Mathematics and Statistics, Virtual University of Pakistan, Lahore, 54000, Pakistan.3_{Department of Mathematics and} Informatics, Lucian Blaga University of Sibiu, Str. Dr. I. Ratiu, No. 5-7, Sibiu, 550012, Romania.4_{Center for Advanced Studies} in Pure and Applied Mathematics, Bahauddin Zakariya University, Multan, 60800, Pakistan. 5_{Department of Mathematics,} Dong-A University, Busan, 49315, Korea.

Acknowledgements

The authors would like to thank the editor and the referees for useful comments and suggestions. This work was supported by the Dong-A University research fund.

Received: 26 February 2016 Accepted: 19 June 2016

References

1. Lupa¸s, A: Aq-analogue of the Bernstein operator. In: Seminar on Numerical and Statistical Calculus, vol. 9, pp. 85-92. University of Cluj-Napoca, Cluj-Napoca (1987)

2. Aral, A, Gupta, V, Agarwal, RP: Applications ofq-Calculus in Operator Theory. Springer, New York (2013) 3. Acu, AM: Stancu-Schurer-Kantorovich operators based onq-integers. Appl. Math. Comput.259, 896-907 (2015).

doi:10.1016/j.amc.2015.03.032

4. Acar, T, Aral, A: On pointwise convergence ofq-Bernstein operators and theirq-derivatives. Numer. Funct. Anal. Optim.36(3), 287-304 (2015). doi:10.1080/01630563.2014.970646

5. Acu, AM, Muraru, CV: Approximation properties of bivariate extension ofq-Bernstein-Schurer-Kantorovich operators. Results Math.67(3-4), 265-279 (2015). doi:10.1007/s00025-015-0441-7

6. Agratini, O: On aq-analogue of Stancu operators. Cent. Eur. J. Math.8(1), 191-198 (2010). doi:10.2478/s11533-009-0057-9

7. Kang, SM, Acu, AM, Rafiq, A, Kwun, YC: Approximation properties ofq-Kantorovich-Stancu operator. J. Inequal. Appl.

2015, 211 (2015). doi:10.1186/s13660-015-0729-x

8. Kang, SM, Acu, AM, Rafiq, A, Kwun, YC: Onq-analogue of Stancu-Schurer-Kantorovich operators based onq-Riemann integral. J. Comput. Anal. Appl.21(3), 564-577 (2016)

9. Ulusoy, G, Acar, T:q-Voronovskaya type theorems forq-Baskakov operators. Math. Methods Appl. Sci. (2015). doi:10.1002/mma.3784

10. Burban, I: Two-parameter deformation of the oscillator algebra and (p,q)-analog of two-dimensional conformal field theory. J. Nonlinear Math. Phys.2(3-4), 384-391 (1995). doi:10.2991/jnmp.1995.2.3-4.18

11. Sahai, V, Yadav, S: Representations of two parameter quantum algebras andp,q-special functions. J. Math. Anal. Appl.

335, 268-279 (2007). doi:10.1016/j.jmaa.2007.01.072

12. Mursaleen, M, Ansari, KJ, Khan, A: Erratum to ‘On (p,q)-analogue of Bernstein operators’ [Appl. Math. Comput. 266 (2015) 874-882]. Appl. Math. Comput.278, 70-71 (2016). doi:10.1016/j/amc.2015.04.090

13. Mursaleen, M, Nasiruzzaman, M, Khan, A, Ansari, KJ: Some approximation results on Bleimann-Butzer-Hahn operators defined by (p,q)-integers. Filomat30(3), 639-648 (2016). doi:10.2298/FIL1603639M

14. Acar, T: (p,q)-Generalization of Szász-Mirakyan operators. Math. Methods Appl. Sci. (2015). doi:10.1002/mma.3721 15. Oru, H, Phillips, GM: A generalization of the Bernstein polynomials. Proc. Edinb. Math. Soc.42, 403-413 (1999).

doi:10.1017/S0013091500020332

16. Ditzian, Z, Totik, V: Moduli of Smoothness. Springer, New York (1987)

17. Finta, Z: Remark on Voronovskaja theorem forq-Bernstein operators. Stud. Univ. Babe¸s-Bolyai, Math.56(2), 335-339 (2011)

18. King, JP: Positive linear operators which preservex2_{. Acta Math. Hung.99, 203-208 (2003).} doi:10.1023/A:1024571126455